• Закон динаміки точки у неінерціальних системах відліку

Отже, всі існуючі системи відліку належать до неінерціальних, а ІСВ – абстракція наше завдання полягає в одержанні основного закону динаміки НІСВ у загальному випадку.

Як показано на Мал.1.11.1, з центром мас Сонця зв’яжемо інерціальну систему відліку (система координат OXYZ), а наявність у Землі багатьох прискорень дозволяє зв’язати з нею неінерціальну систему відліку найзагальнішого типу. При цьому не виходитимемо за межі класичної механіки, вважаючи однаковими інтервали часу і відстані, а також сили взаємодії тіл в обох системах відліку.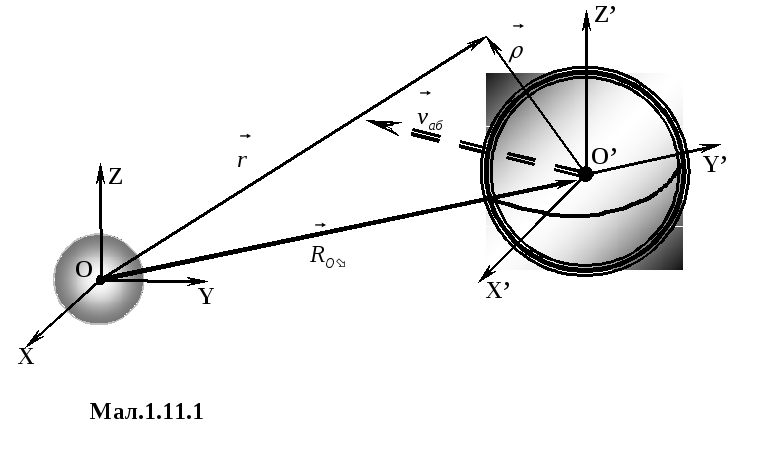

Рухома неінерціальна система координат має початок відліку у центрі Землі, вісь напрямлена уздовж вектора миттєвої кутової швидкості нашої планети, осі і лежать у площині екватора (Мал.1.11.1). Ця система координат жорстко зв’язана із земною кулею, здійснюючи разом з нею рух навколо Сонця. Власне і прецесійне обертання тощо.

Матеріальна точка масою рухається по поверхні Землі, а її положення в НІСВ визначається змінним вектором , проведеним у точку розташування з центра планети. Положення у ІСВ визначається вектором , а траєкторія руху може бути визначена для конкретних початкових умов шляхом інтегрування диференційного рівняння другого закону Ньютона в інерціальній системі відліку:

(1.11.1)

Де – прискорення точки відносно інерціальної системи відліку (“абсолютне” прискорення ; – сили взаємодії матеріальної точки з оточуючими тілами, зокрема, і – сили гравітаційного притягання до Сонця і Землі, – сила опору середовища, – сила нормальної реакції опори тощо.

Основний закон динаміки точки в НІСВ одержимо з рівняння (1.11.1) шляхом введення у нього другої похідної по часу від відносного радіуса-вектора . З Мал.1.11.1 випливає, що

=+

(1.11.2)

Радіус-вектор точки відносно ІСВ є векторною сумою відносного радіуса-вектора і вектора , що визначає положення центра Землі відносно ІСВ.

Позначимо через мале переміщення частинки відносно центра мас Сонця. З мал.1.11.1 випливає, що у загальному випадку його можна записати як суму трьох векторів, які відповідають переміщенням із-за частинних рухів:

=++

(1.11.3)

Де – мале переміщення частинки разом із Землею у її поступальному русі навколо Сонця;

– поворотне переміщення відносно ІСВ внаслідок обертання НІСВ (обертання Землі навколо власної осі, як показано на Мал.1.11.2); частинка матиме вказані переміщення навіть у тому випадку, коли вона закріплена на поверхні Землі; – переміщення матеріальної точки внаслідок її руху відносно НІСВ, яке називатимемо відносним переміщенням.

Ввівши вектор нескінченно малого повороту НІСВ, модуль якого дорівнює куту повороту, а напрям співпадає з віссю обертання Землі, запишемо поворотне переміщення як векторний добуток (див. Мал.1.11.2), що приводить формулу (1.11.3) до наступного вигляду:

=++

(1.11.3а)

Поділивши цю рівність на інтервал часу , протягом якого відбулось переміщення, шляхом переходу до межі , одержимо вираз для абсолютної швидкості матеріальної точки відносно ІСВ через характеристики руху НІСВ та відносну швидкість :

++

(1.11.4)

Де – вектор кутової швидкості обертання НІСВ;

– швидкість поступального руху НІСВ;

– швидкість переносу точки внаслідок обертання НІСВ;

– відносна швидкість точки по поверхні Землі.

Суму + перших двох складових у (1.11.4) називають переносною швидкістю частинки. означає, що зміна розглядається відносно нерухомої Землі, яка не обертається навколо власної осі. Таку похідну називатимемо “відносною”, оскільки вона обчислюється в НІСВ.

Для обчислення абсолютної швидкості відносно ІСВ можна взяти похідну від радіуса-вектора , що визначається (1.11.2):

(1.11.5)

Тут абсолютна похідна обчислюється відносно ІСВ. Порівнюючи (1.11.4) і (1.11.5), одержимо формулу зв’язку абсолютного і відносного диференціювання:

(1.11.6)

Вона свідчить, що абсолютна похідна довільного вектора , визначеного в НІСВ, дорівнює сумі векторного добутку кутової швидкості неінерціальної системи відліку на цей вектор і відносної похідної цього вектора, яка обчислюється в НІСВ так, наче ця система відліку нерухома і належить до класу інерціальних. Зміст (1.11.6) стане зрозумілішим, якщо згадати, що з точки зору спостерігача в ІСВ зміни вектора (Мал.1.11.1) викликаються двома причинами: його поворотом через обертання НІСВ та рухом матеріальної точки відносно неінерціальної системи відліку. Формула (1.11.6) враховує обидві причини. Вона важлива у тому відношенні, що дозволяє обчислити в ІСВ похідну довільного вектора, заданого розкладом на складові уздовж осей рухомої системи координат .

Для обчислення абсолютного прискорення , що входить у рівняння динаміки (1.11.1), про диференціюємо (1.11.4):

=+++

(1.11.7)

У правій частині (1.11.7) присутні два вектори і , які визначені відносно НІСВ, тому при обчисленні похідних від цих векторів необхідно застосувати (1.11.6). Виконавши нескладні алгебраїчні перетворення, маємо формулу для абсолютного прискорення:

=++++

(1.11.8)

Де абсолютне прискорення;

;

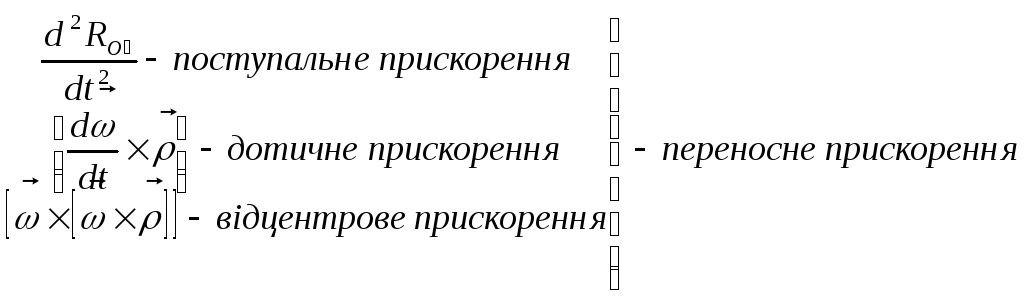– прискорення Коріоліса; – відносне прискорення.

Якщо підставити (1.11.8) у рівняння динаміки (1.11.1), то маємо:

++++=

(1.11.9)

Отже, заміна вектора на суму і спричинила заміну вектора абсолютного прискорення на суму п’яти прискорень. Перші три з них, що складають у сумі переносне прискорення, являють собою прискорення тієї точки НІСВ, яку у даний момент займає частинка . Прискорення Коріоліса має комбінований характер, бо визначається кутовою швидкістю НІСВ і відносною швидкістю частинки і не залежить від положення її в НІСВ.

Диференціальне рівняння (1.11.9) має звичну структуру: ліва його частина складається з добутків маси частинки на прискорення, права – з сил її взаємодії з оточуючими тілами. Шуканий закон руху матеріальної точки у НІСВ одержимо з (1.11.9) тоді, коли перенесемо у праву його частину з лівої чотири з п’яти складових, залишивши в ній лише добуток маси частинки на вектор відносного прискорення, що дозволить надати йому такого ж вигляду, який мало вихідне рівняння (1.11.1) руху відносно ІСВ:

=----+

(1.11.10)

Диференціальне рівняння другого порядку (1.11.10) називається рівнянням динаміки матеріальної точки в НІСВ.

З рівняння (1.11.10) випливає, що навіть цілком вільна частинка, для якої дорівнює нулю векторна сума сил її взаємодії з оточуючими тілами (=0), по відношенню до НІСВ завжди буде рухатись прискорено, що означає повну непридатність закону інерції Ньютона до неінерціальних систем відліку. Для спостерігача в неінерціальній системі відліку ситуація виглядає так, наче на таку частинку діють чотири сили, що зумовлюють її прискорений рух. Чотири добутки маси частинки на прискорення у правій частині рівняння (1.11.10) називатимемо силами інерції в НІСВ, коротко – сили інерції.