
- •Збірник задач
- •Передмова
- •Робоча програма дисципліни «Фізика»
- •Як правильно оформляти задачі і контрольну роботу в цілому?
- •Київський національний Університет Будівництва і архітектури Кафедра фізики
- •Модуль 1 «Механіка»
- •1.1. Короткий теоретичний довідник до модуля 1.
- •1.2. Задачі до модуля 1
- •Модуль 2 «Молекулярна фізика»
- •2.1. Короткий теоретичний довідник до модуля 2
- •2.2. Задачі до модуля 2
- •Модуль 3 «Електрика та магнетизм»
- •3.1. Короткий теоретичний довідник до модуля 3
- •3.2. Задачі до модуля 3
- •Модуль 4 «Коливальні та хвильові процеси, оптика»
- •4.1. Короткий теоретичний довідник до модуля 4
- •4.1.А. Короткий теоретичний довідник до теми «Геометрична оптика»
- •4.2. Задачі до модуля 4
- •4.2.А. Задачі до теми «Геометрична оптика»
- •Модуль 5 «Основи квантової фізики та фізики ядра»
- •5.1. Короткий теоретичний довідник до модуля 5
- •5.2. Задачі до модуля 5
- •Список літератури
- •Основні одиниці Міжнародної системи (сі)
- •Основні фізичні сталі
- •Деякі позасистемні величини
- •Деякі співвідношення між фізичними величинами
- •Деякі астрономічні величини
- •Властивості деяких твердих тіл
- •Властивості деяких рідин
- •Густина газів (за нормальних умов), кг/м3
- •Густина (середня насипна) деяких будівельних матеріалів, кг/м3
- •Густина деяких речовин і матеріалів, кг/м3
- •Пружні властивості деяких твердих тіл
- •Модуль Юнга деяких матеріалів, Гпа
- •Границя міцності деяких матеріалів, Гпа
- •Залежність відносних долей молекул за розподілом Максвела від відносної швидкості
- •Залежність долі молекул, швидкості яких перевищують задане значення відносної швидкості
- •Питома теплота згоряння деяких видів палива, мДж/кг
- •Питома теплота плавлення і температура плавлення деяких речовин, металів та сплавів (за нормального атмосферного тиску)
- •Температурний коефіцієнт лінійного розширення деяких речовин
- •Питома теплота пароутворення води при різних температурах
- •Критичні значення температури та тиску для деяких речовин
- •Діелектрична проникність деяких речовин
- •Робота виходу електронів з металів
- •Маса і енергія спокою деяких частинок
- •Маса деяких нуклідів, а.О.М.
- •Енергія іонізації
- •Десяткові префікси до назв одиниць
- •Графік залежності коефіцієнта поглинання -випромінювання від енергії падаючого кванта для різних речовин
Модуль 1 «Механіка»
1.1. Короткий теоретичний довідник до модуля 1.
Кінематичне рівняння поступального руху матеріальної точки визначається як:
![]()
 ,
,
де
![]() –
радіус-вектор матеріальної точки,У
декартовій системі координат:
–
радіус-вектор матеріальної точки,У
декартовій системі координат:
![]() .
.
Швидкість
є похідною від радіус-вектора рухомої
точки за часом:
![]() і завжди орієнтована по дотичній до
траєкторії. Вектор швидкості в проекціях
наосі
координат осі має вигляд:
і завжди орієнтована по дотичній до
траєкторії. Вектор швидкості в проекціях
наосі
координат осі має вигляд:
![]() .
Абсолютне значення (модуль) швидкості
визначається як:
.
Абсолютне значення (модуль) швидкості
визначається як:![]() .
.
П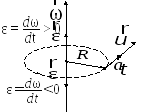 рискорення
точки визначається за формулою:
рискорення
точки визначається за формулою: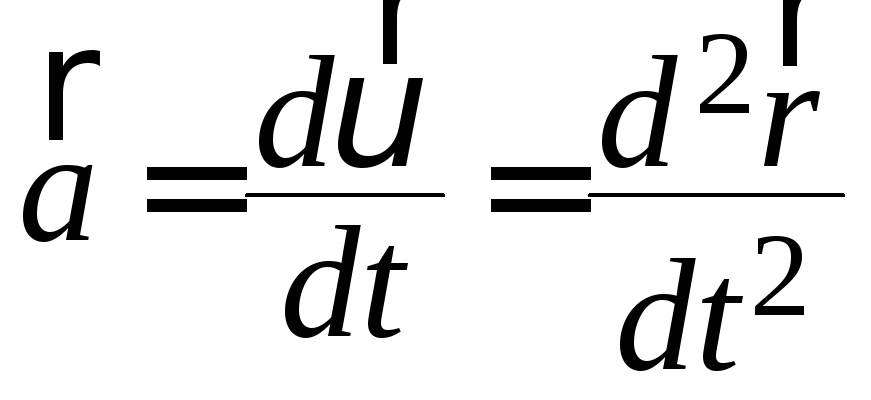 .
Повне прискорення при криволінійному
русі може бути розкладене на дві складові:
.
Повне прискорення при криволінійному
русі може бути розкладене на дві складові:![]() ,
де
,
де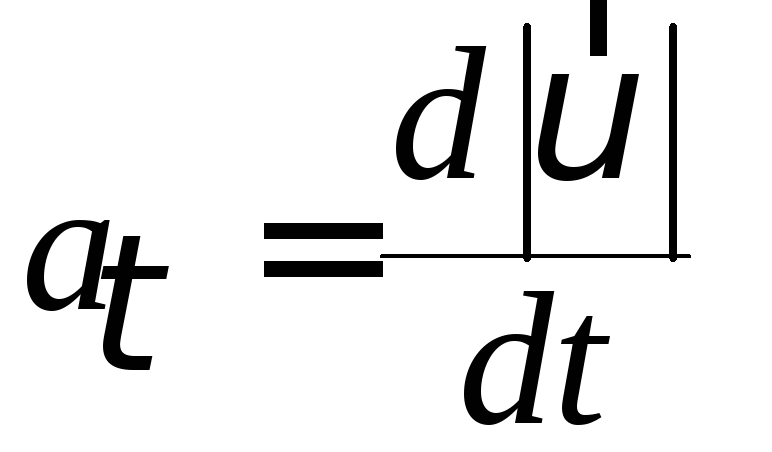 –
тангенціальне прискорення;
–
тангенціальне прискорення;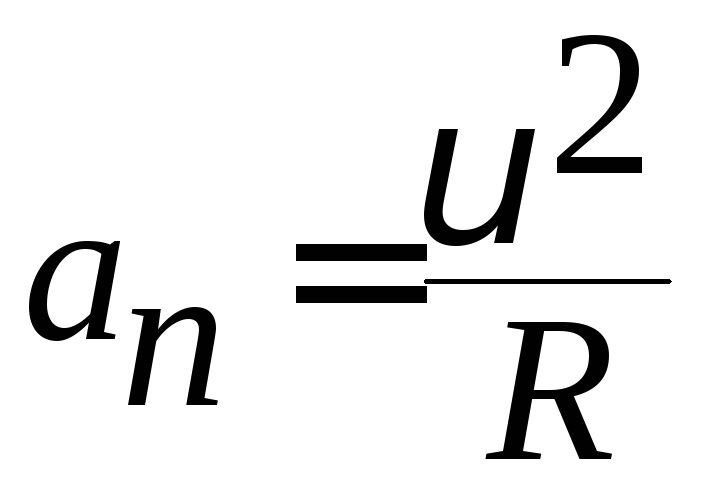 – нормальне (доцентрове) прискорення.
Модуль повного прискорення визначається
за формулою:
– нормальне (доцентрове) прискорення.
Модуль повного прискорення визначається
за формулою:![]() .
.
Кінематичне
рівняння руху матеріальної точки по
колу (обертального руху абсолютно
твердого тіла (АТТ)):
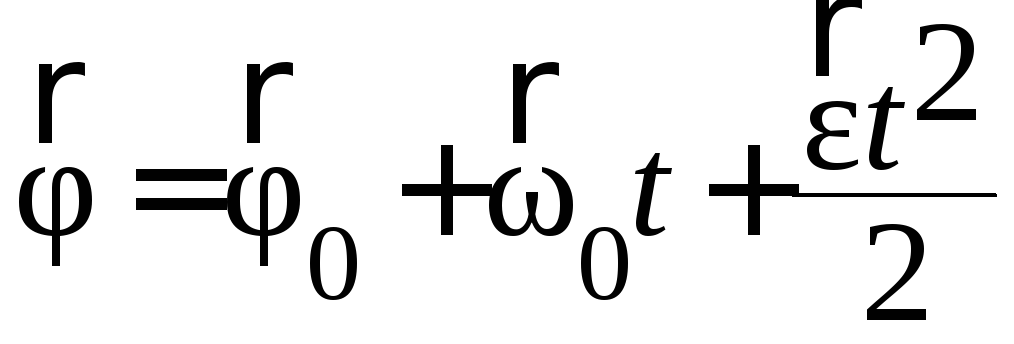 ,
де
,
де![]() – кут повороту тіла навколо осі в момент
часу t.
Вектори кутової швидкості та кутового
прискорення визначаються відповідно
як:
– кут повороту тіла навколо осі в момент
часу t.
Вектори кутової швидкості та кутового
прискорення визначаються відповідно
як:
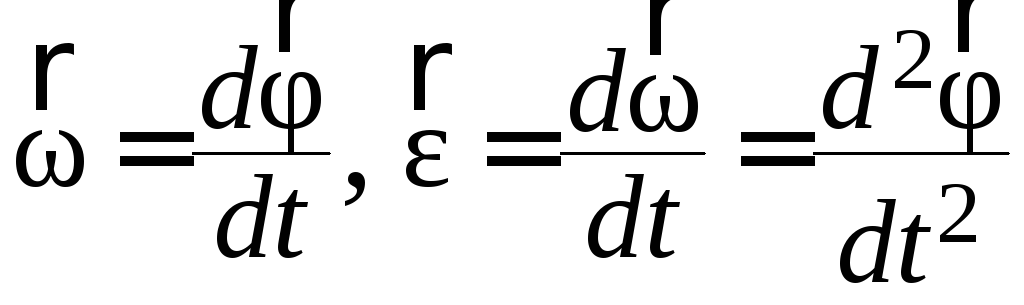 .
Кутові та лінійні характеристиками
обертання пов’язані співвідношеннями:
.
Кутові та лінійні характеристиками
обертання пов’язані співвідношеннями:![]() ,
,![]() ,
,![]() .
.
Закон динаміки
поступального руху матеріальної точки
(ІІ
закон Ньютона)
має вигляд:
![]() ,
де
,
де![]() – імпульс (кількість руху) матеріальної
точки масоюm,
– імпульс (кількість руху) матеріальної
точки масоюm,
![]() – векторна сума сил, що діють на
матеріальну точку. Для випадків, при
яких маса
– векторна сума сил, що діють на
матеріальну точку. Для випадків, при
яких маса![]() ,
можна записати:
,
можна записати: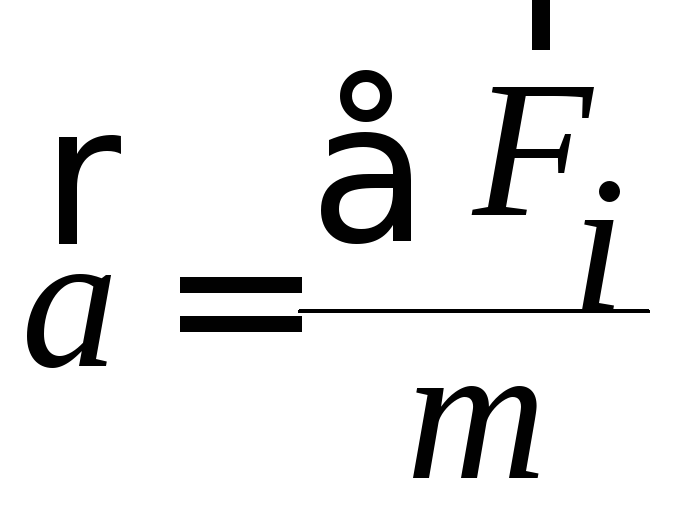 ,
де
,
де![]() –
прискорення.
–
прискорення.
Сила пружності,
що виникає під час деформації тіла
вздовж осі ох,
визначається за законом Гука:
![]() ,
де k
– коефіцієнт
пружності (у випадку з пружиною –
жорсткість); х
– абсолютна
деформація. Гравітаційна сила F,
яка діє між двома матеріальними точками,
визначається законом всесвітнього
тяжіння:
,
де k
– коефіцієнт
пружності (у випадку з пружиною –
жорсткість); х
– абсолютна
деформація. Гравітаційна сила F,
яка діє між двома матеріальними точками,
визначається законом всесвітнього
тяжіння:
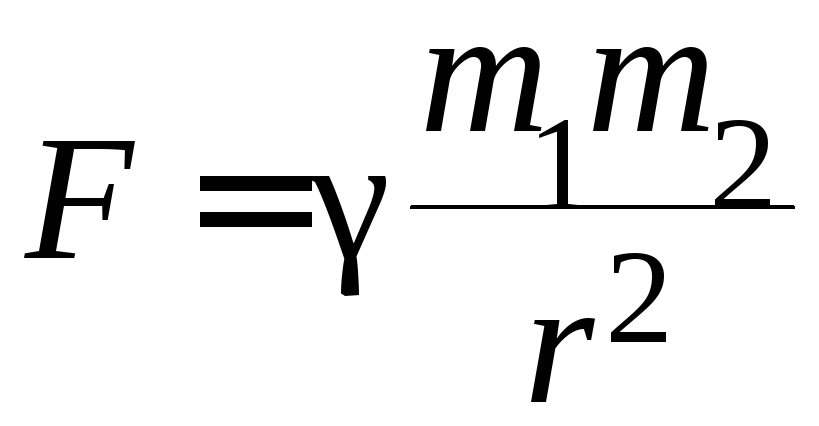 ,
де
γ = 6,67∙10–11 Н∙м2/кг2
– гравітаційна постійна, m1,
m2
– маси взаємодіючих тіл, r – відстань
між ними. Сила тертя ковзання
,
де
γ = 6,67∙10–11 Н∙м2/кг2
– гравітаційна постійна, m1,
m2
– маси взаємодіючих тіл, r – відстань
між ними. Сила тертя ковзання
![]() ;
– коефіцієнт тертя; N
– сила нормального тиску.
;
– коефіцієнт тертя; N
– сила нормального тиску.
За законом збереження
імпульсу сумарний імпульс замкненої
системи, що складається з n
матеріальних точок, залишається
незмінним:
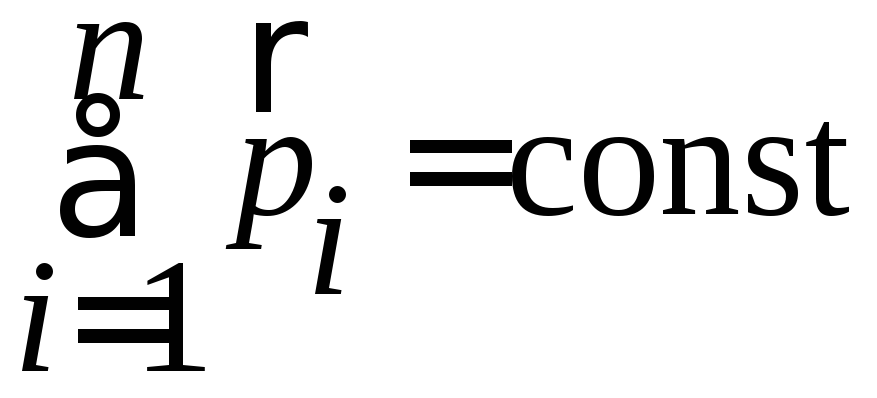 .
Радіус-вектор центра мас системи
матеріальних точок визначається як
.
Радіус-вектор центра мас системи
матеріальних точок визначається як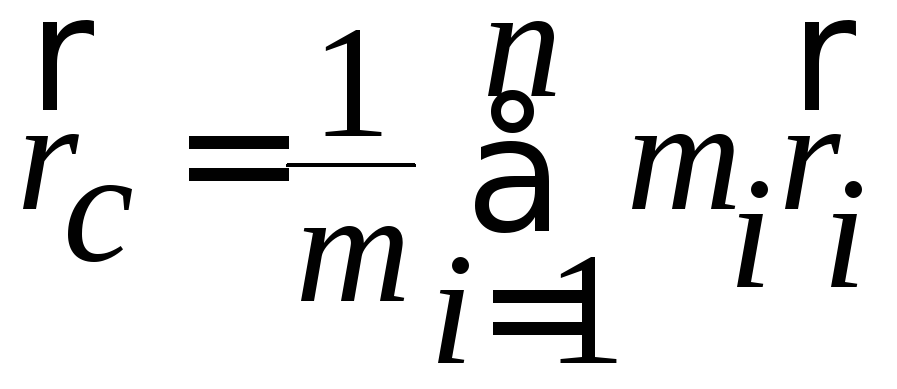 ,
деm
– сума мас усіх точок (маса системи); mi
i
,
деm
– сума мас усіх точок (маса системи); mi
i
![]() –
маса і радіус-векторі-ї
матеріальної точки системи.
–
маса і радіус-векторі-ї
матеріальної точки системи.
Рух тіл змінної
маси визначається рівнянням Мещерського:
![]() ,
де
,
де
![]() – реактивна сила,
– реактивна сила,![]() – швидкість витоку газів. Швидкість
ракети в кінці стадії розгону визначається
за формулою Ціолковського:
– швидкість витоку газів. Швидкість
ракети в кінці стадії розгону визначається
за формулою Ціолковського:
![]() ,
де υ
– кінцева швидкість ракети, m0/m
– відношення мас ракети
на старті та наприкінці розгону.
,
де υ
– кінцева швидкість ракети, m0/m
– відношення мас ракети
на старті та наприкінці розгону.
Закон динаміки
обертального руху АТТ:
![]() ,
де
,
де![]() – момент
сили відносно осі,
– момент
сили відносно осі,
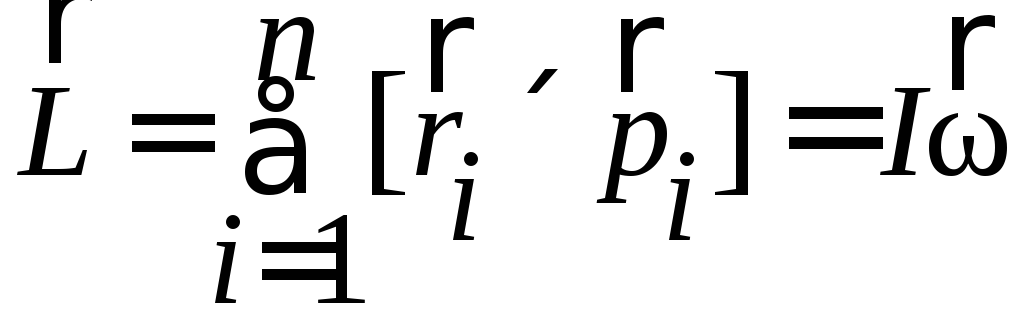 – момент імпульсу тіла,
– момент імпульсу тіла,
 – момент
інерції тіла
відносно осі,
mi
– елементарні маса,
– момент
інерції тіла
відносно осі,
mi
– елементарні маса,
![]() –
її відстань від осі обертання.
У випадку
–
її відстань від осі обертання.
У випадку
![]() закон
динаміки обертального руху має вигляд:
закон
динаміки обертального руху має вигляд:
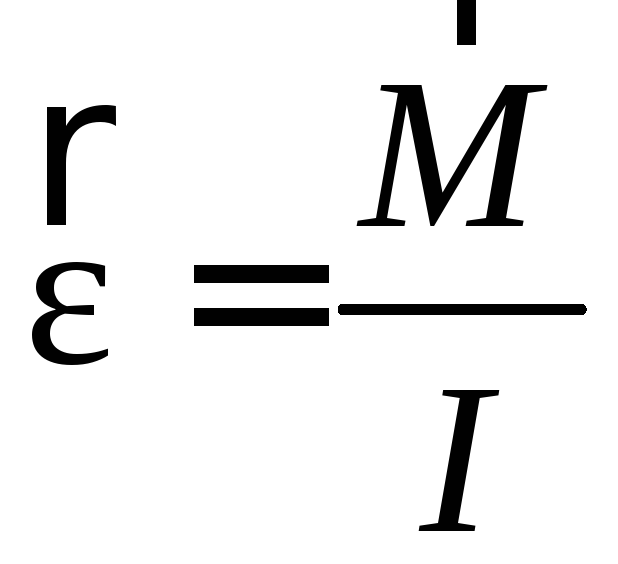 ,
Закон збереження моменту імпульсу:
,
Закон збереження моменту імпульсу:
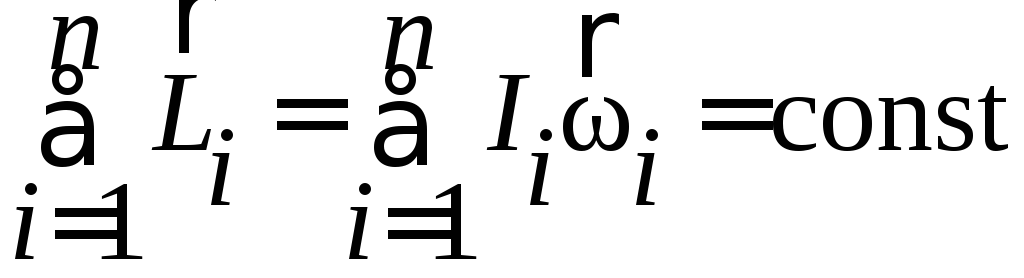 справедливий
для замкнених систем.
справедливий
для замкнених систем.
Момент інерції
тіл різної форми: стрижня довжиною l
та масою m
відносно осі, що проходить через центр
мас перпендикулярно до стрижня:
![]() ;
диска радіусомR
відносно осі, що проходить через центр
диска і перпендикулярної до його площини:
;
диска радіусомR
відносно осі, що проходить через центр
диска і перпендикулярної до його площини:
 ;
кулі радіусомR
відносно осі, що проходить через його
центр:
;
кулі радіусомR
відносно осі, що проходить через його
центр:
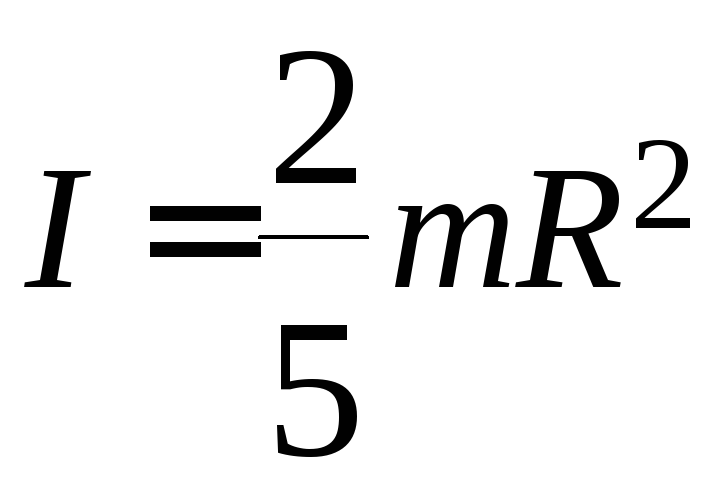 .
.
Умова рівноваги твердого тіла: векторна сума всіх зовнішніх сил, що діють на тіло, а також усіх моментів цих сил, рівна нулеві:

Зміна енергії тіла
визначається роботою сили
![]() ,
де
,
де![]() – переміщення тіла. Потужність – робота,
що виконується за одиницю часу:
– переміщення тіла. Потужність – робота,
що виконується за одиницю часу: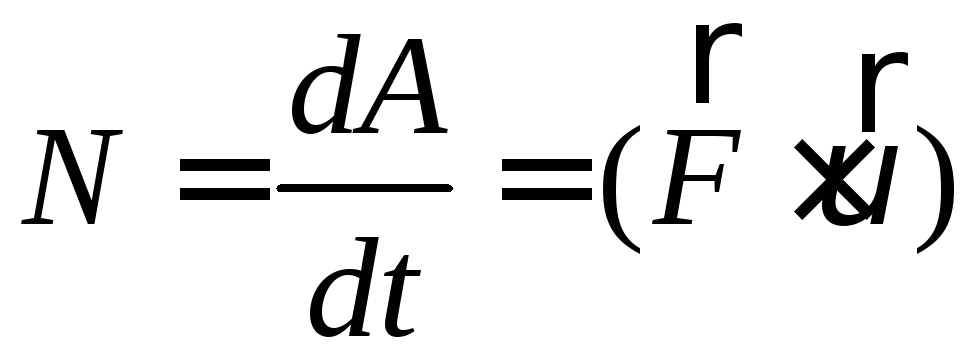 .
.
За законом збереження
механічної енергії в замкнених
консервативних системах тіл повна
механічна енергія зберігається з часом:
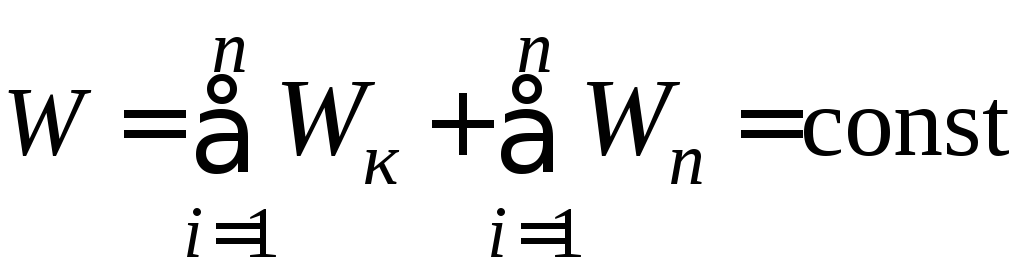 .
.
Кінетична енергія
поступального руху тіла:
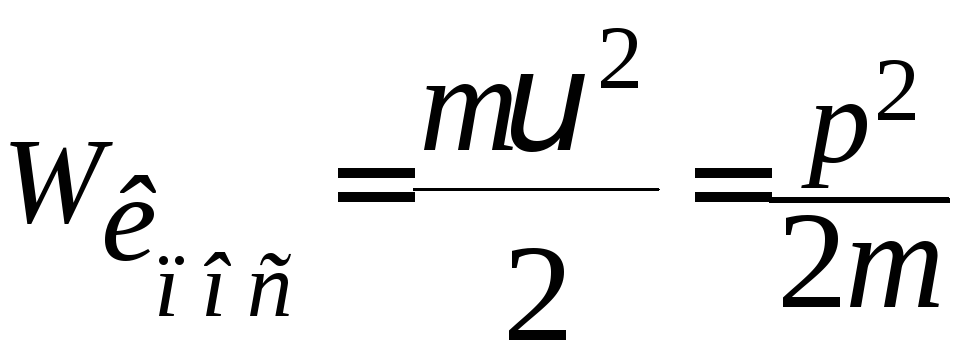 .
Кінетична енергія обертального руху
тіла:
.
Кінетична енергія обертального руху
тіла: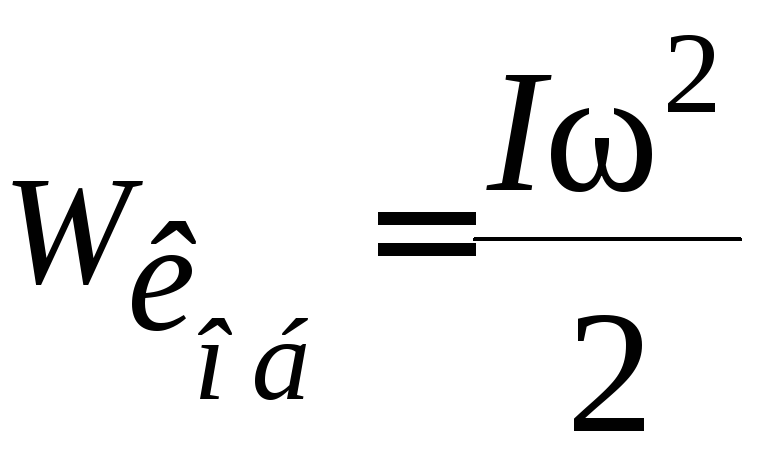 .
Потенціальна енергія пружно деформованої
пружини
.
Потенціальна енергія пружно деформованої
пружини ;k
– жорсткість пружини; х
– абсолютна деформація. Потенціальна
енергія гравітаційної взаємодії двох
матеріальних точок:
;k
– жорсткість пружини; х
– абсолютна деформація. Потенціальна
енергія гравітаційної взаємодії двох
матеріальних точок:
![]() .
.
Течія ідеальної
рідини описується рівнянням Бернуллі:
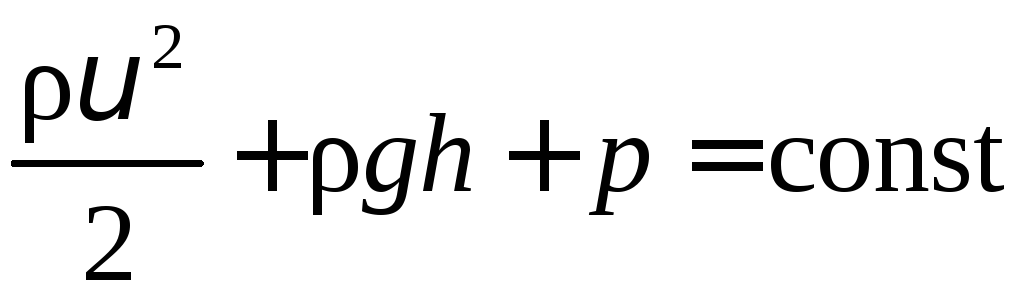 ,
де
– густина рідини; υ – швидкість рідини
в певному перерізі труби; h
– висота, на якій розміщено переріз; р
– статичний тиск рідини для обраного
перерізу. Рівняння нерозривності течії
має вигляд:
,
де
– густина рідини; υ – швидкість рідини
в певному перерізі труби; h
– висота, на якій розміщено переріз; р
– статичний тиск рідини для обраного
перерізу. Рівняння нерозривності течії
має вигляд:
![]() ,
деS
– площа перерізу в будь-якому місці
труби,
,
деS
– площа перерізу в будь-якому місці
труби,
![]() –
швидкість руху рідини в цьому перерізі.
–
швидкість руху рідини в цьому перерізі.
За формулою Пуазейля
об’єм в’язкої рідини, що протікає
трубкою:
![]() ,
деR
– радіус трубки; р
– різниця
тисків на кінцях трубки; l
– її довжина; –
коефіцієнт динамічної в’язкості, t
– час. Сила в’язкого тертя, що діє на
сферичне тіло
в потоці
рідини (газу) визначається формулою
Стокса:
,
деR
– радіус трубки; р
– різниця
тисків на кінцях трубки; l
– її довжина; –
коефіцієнт динамічної в’язкості, t
– час. Сила в’язкого тертя, що діє на
сферичне тіло
в потоці
рідини (газу) визначається формулою
Стокса:
![]() ,
деR
– радіус
кульки;
,
деR
– радіус
кульки;
![]() – її швидкість.
– її швидкість.
Лоренцове скорочення
довжини тіла визначається як:
![]() ,l0 –
довжина тіла в нерухомій (лабораторній)
системі відліку, β=υ/с;
с = 3∙108 м/с –
швидкість світла у вакуумі. Інтервал
часу між подіями, виміряний у рухомій
системі відліку визначається як:
,l0 –
довжина тіла в нерухомій (лабораторній)
системі відліку, β=υ/с;
с = 3∙108 м/с –
швидкість світла у вакуумі. Інтервал
часу між подіями, виміряний у рухомій
системі відліку визначається як:
 ,о –час,
виміряний у нерухомій (лабораторній)
системі відліку. Релятивістський закон
додавання швидкостей має вигляд:
,о –час,
виміряний у нерухомій (лабораторній)
системі відліку. Релятивістський закон
додавання швидкостей має вигляд:
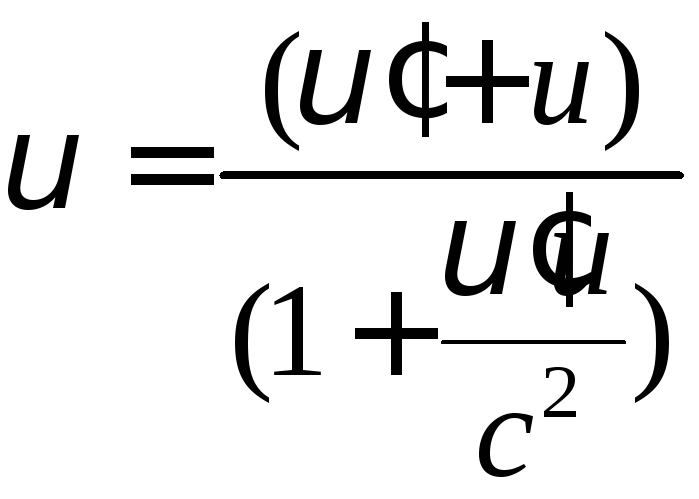 ,
,![]() та
та![]() –
відповідно швидкість тіла відносно
нерухомої та рухомої системи відліку;u
– швидкість рухомої системи відліку
відносно нерухомої.
–
відповідно швидкість тіла відносно
нерухомої та рухомої системи відліку;u
– швидкість рухомої системи відліку
відносно нерухомої.
Релятивістський
імпульс:
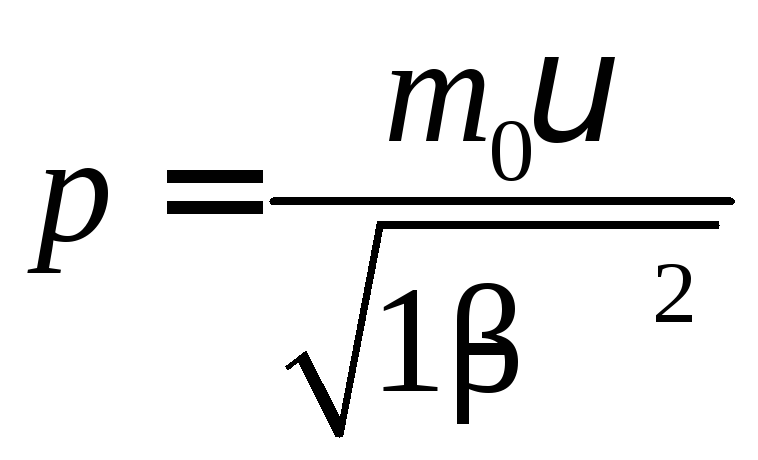 ,
деm0
– маса спокою тіла. Релятивістська маса
тіла:
,
деm0
– маса спокою тіла. Релятивістська маса
тіла:
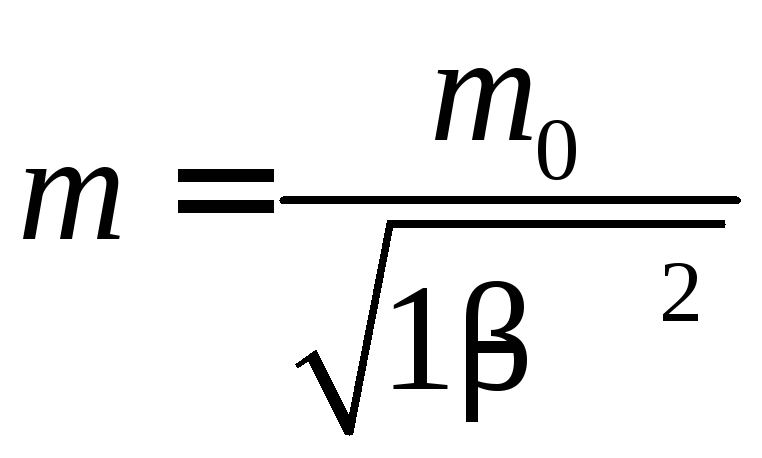 .
.
Повна
енергія
тіла в релятивістській механіці:
![]() .Енергія
спокою тіла:
.Енергія
спокою тіла:
![]() .
Кінетична енергія тіла:
.
Кінетична енергія тіла:![]() .
Зв’язок між повною енергієюW
та імпульсом р
в релятивістській механіці:
.
Зв’язок між повною енергієюW
та імпульсом р
в релятивістській механіці:
![]() .
.
