3.10. Завдання для виконання розрахункової роботи

Задача № 1. Повний розрахунок статично визначеної балки при згині.

Для заданих двох схем балок (рис. 3.13) зробити повний розрахунок на міцність та жорсткість. Вибрати круглий, прямокутний і двотавровий поперечний переріз по нормальним напруженням та порівняти ваги балок, прийнявши вагу двотаврової балки за 100%. Методом початкових параметрів визначити прогин у балки в середині прогону та на вільних кінцях. Матеріал балок - Ст3; [σ] = 160 МПа; [τ] = 100 МПа; [f] = 2 см. Необхідні дані взяти з таблиці 3.1.

Таблиця 3.1

Номер рядка	Номер схеми	М, кНм	ЛкН	Я, кН/м
1	І	1	10	1
2	II	2	9	2
3	III	3	8	3
4	IV	4	7	4
5	V	5	6	5
6	VI	6	5	4
7	VIII	7	4	3
8	VIII	8	3	2
9	ІХ	9	2	1
10	X	10	1	10

Задача № 2. Розрахунок статично невизначеної балки при згині.

Для даної балки (рис. 3.14) підібрати двотавровий поперечний переріз по нормальним напруженням, якщо [σ] = 160 МПа. Необхідні дані взяти із таблиці 3.1

Рис. 3.13. Схеми балок для виконання задачі №1

Рис. 3.13. (продовження)

Рис. 3.14. Розрахункова схема балки

3.11. Рівняння трьох моментів для нерозрізних балок

Нерозрізними називають балки, що упираються на більше ніж дві опори (рис. 3.15).

Рис. 3.15. Схема нерозрізної балки

Як видно з рисунку, кількість зайвих зв’язків, а отже, і зайвих реакцій, дорівнює кількості проміжних опор.

Для утворення основної системи можна звільнитися від усіх проміжних опор, замінивши їх дію невідомими реакціями Х₂, Х₃, Х₄, прикладеними до основної системи додатково до заданого навантаження. Додаткові рівняння переміщень будуть мати вид: Δ₂ = 0; Δ ₃ = 0; Δ ₄ = 0. Однак такий спосіб розрахунку громіздкий, оскільки в кожне рівняння входять усі шукані невідомі зусилля. Значно вигідніше будувати основну систему встановленням шарнірів у перерізах над усіма проміжними опорами. Зайвими невідомими в цьому разі будуть згинальні моменти в опорних перерізах балки. Напрями моментів для певності вибирають додатними. При такому виборі основної системи дія заданого навантаження поширюється тільки на той проліт, де воно прикладається (вплив його на інші прольоти визначається опорними згинальними моментами).

Дійсно, кожна двохопорна балка основної системи під дією заданого навантаження та опорних моментів деформується незалежно від інших. Це означає, що торці двох суміжних балочок, що примикають до однієї опори можуть повернутися на деякі кути φ_лів та φ_пр (рис. 3.16).

Оскільки у вихідній статично невизначеній системі кожна пара таких перерізів становить один переріз, то з умов суцільності їх взаємний кут повороту має дорівнювати нулю.

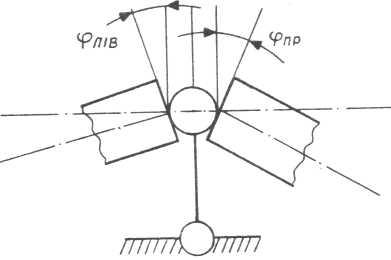
Рис. 3.16. Схема опори балки

Таким чином, для кожної проміжної опори:

. (3.24)

Оскільки основна система складається з окремих, не зв’язаних між собою двохопорних балочок, то для розкриття умови (3.24) слід розглянути лише два прольоти основної системи, що примикають до «n»-ї опори (рис. 3.17).

Рис. 3.17. Розрахункова схема

Умова (3.24) в канонічному вигляді для середньої опори така:

;

Визначаючи переміщення графоаналітичним методом або застосовуючи спосіб Верещагіна, одержуємо кінцеву формулу чи кінцеве рівняння, яке називається рівнянням трьох моментів:

. (3.25)

У цьому рівнянні: М_лів - момент на лівій опорі; l_лів - довжина лівого прольоту; М_ср - момент на середній опорі; l_пр - довжина правого прольоту; М_пр - довжина правого прольоту; - фіктивна реакція від фіктивного навантаження на середній опорі. За фіктивне навантаження приймається епюра згинаючих моментів на кожному прольоті.

Рівняння трьох моментів можна скласти для будь-яких двох сусідніх прольотів.

В даному випадку їх можна скласти три. Таким чином статично невизначена система буде вирішена.

Порядок розрахунку нерозрізної балки наступний.

Пронумерувавши опори та прольоти багатопрольотної нерозрізної балки зображують основну систему, навантажену заданим навантаженням та невідомими опорними моментами.

Якщо якийсь кінець багатопрольотної балки затиснутий, то затиснення в основній системі треба замінити додатковим прольотом нескінченно великої жорсткості або нескінченно малої довжини. Далі треба побудувати епюри М для окремих балочок основної системи тільки від заданого навантаження на прольотах та знайти на середній опорі (обчисливши площі цих епюр та координати їхніх центрів ваги). Записати рівняння трьох моментів для будь-яких двох сусідніх прольотів.

Розв'язуючи систему рівнянь трьох моментів, знаходяться невідомі опорні моменти. Потім необхідно визначити значення та напрям опорних реакцій за допомогою метода поперечних перерізів та рівнянь рівноваги. Знаючи значення опорних реакцій можна побудувати епюри поперечних сил та згинальних моментів і зробити необхідні розрахунки на міцність та жорсткість.