3.3. Епюри поперечних сил і згинальних моментів

Приклад 1. Побудувати епюри Q та М для балки, схема якої показана на рис. 3.4.

1. Визначимо опорні реакції. Напрям опорних реакцій вибирається довільно. Перше рівняння статики: :

.

В цьому рівнянні момент за годинниковою стрілкою додатний, проти - від’ємний:

Рис. 3.4. Побудова епюр Q та М

Друге рівняння статики: :

:

.

Перевірка: :

.

2. Будуємо епюру поперечних сил. Балка має п’ять ділянок. Записуємо рівняння поперечних сил для кожного з них, та обчислюємо Q у характерних перерізах:

, ,

при _Хі = 0, Q_I = 0; при x₁ = 0,6, ;

, ,

при х₂ = 0, Q_ІІ = 42,2 кН; при х₂=1м, Q_ІІ = 12,2 кН;

Q_V= Р = 40 кН;

Q_ІV = Р –R_В = 40 - 57,8 = -17,8 кН;

, ,

при х₃ = 0, Q_ІІІ = -17,8 кН; при х₃ = 1, Q_ІІІ =12,2 кН.

3. Записуємо рівняння згинальних моментів для кожної з п’яти ділянок та знаходимо М у характерних перерізах:

, ,

при _Хі = 0, М_I = 0; при x₁ = 0,6, ;

, ,

при х₂ = 0, М_IІ = - 5,4 кНм; при х₂ = 1 м, М_IІ = 21,8 кНм.

Тепер краще розглянути п’яту ділянку:

, ,

при х₅ = 0, М_V = 0; при х₅ = 1 м, М_V = - 40 кНм;

, ,

при х₄ = 0, М_ІV = - 40 кНм; при х₄ = 0,5, М_ІУ = 31,1 кНм;

, ,

при х₃ = 0, М_ІІІ = 31,1 кНм; при х₃ = 1 м, М_ІІІ = 28,2 кНм.

На третій ділянці поперечна сила дорівнює нулю. Треба знайти х₃, коли Q_ІІІ = 0. Записуємо рівняння поперечних сил для третьої ділянки та прирівнюємо його нулю:

,

.

Тоді

.

При х₃ = 0,59, = - 25,8 кНм.

Будуємо епюру згинальних моментів М по даним підрахункам.

Розглядаючи епюри Q, М та навантаження на балку з точки зору загальних властивостей епюр, виявляємо, що побудовані епюри не містять принципових помилок: наприклад, усюди, де Q > 0, момент М зростає, а там, де Q < 0 - зменшується; під зовнішнім моментом М на епюрі М має місце стрибок на значення 50 кНм; під реакціями R_А, R_В і зовнішньою силою Р на епюрі Q є також стрибок на значення цих сил; під рівномірно розподіленим навантаженням на епюрі Q - похилі лінії, а на епюрі М - параболи, опуклість яких звернена у бік, протилежний напряму дії навантаження.

Аналізуючи значення поперечних сил і згинальних моменти можна зробити висновок, що під дією даного навантаження на дану балку максимальна поперечна сила дорівнює 42,2 кН та знаходиться в поперечному перерізі на опорі «А"», а максимальний згинальний момент дорівнює 40,0 кН і знаходиться в поперечному перерізі на опорі «В».

Відомо, що від поперечних сил в перерізі залежать дотичні напруги, а від згинальних моментів залежать нормальні напруги. Розподіл дотичних і нормальних напруг в поперечному перерізі балки розглянемо нижче, а зараз побудуємо епюри Q та М для консольної балки, схема якої представлена на рис.3.5.

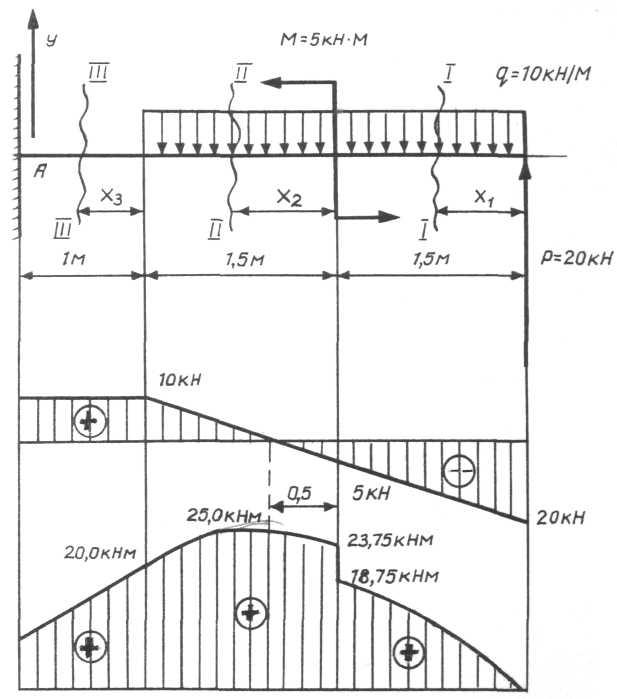
Рис 3.5. Схема до побудови епюр консольної балки

Приклад 2. В даному випадку при побудові епюр Q і М для консольної балки реакції в жорсткому закріпленні знаходити необов’язково. Треба будувати епюри, починаючи з вільного кінця балки. Розглядаючи кожну ділянку, треба відкидати ліву частину балки разом з невідомими реакціями.

Розглянемо першу ділянку:

, ,

при х₁ = 0, 20 кН; Q_І-І = -Р=-20 кН;

при х₁ = 1,5, .

Розглянемо другу ділянку:

, ,

при х₂ = 0, Q_ІІ-ІІ = -5кН;

при х₂ = 1,5, .

Розглянемо третю ділянку:

кН

Будуємо епюру згинальних моментів:

,

при х₁ = 0, М_І-І = 0;

при х₁ = 1,5, кНм;

, ;

при х₂ = 0, кНм;

при х₂ = 1,5, кНм.

На другій ділянці епюра поперечних сил перетинає базову лінію. Тому треба найти на епюрі моментів під точкою перетину. Находимо відстань від початку другої ділянки до точки перетину епюри поперечних сил з базовою лінією:

,

, .

Знаходимо при х₂ = 0,5 м:

кНм.

Викреслюємо епюру згинальних моментів на другій ділянці.

Будуємо епюру згинальних моментів на третій ділянці:

, .

при х₃ = 0, М_{ІІІ-ІІІ} = 20 кНм;

при х₃=1м, кНм.

Побудувавши епюри Q і М і зробивши їх перевірку на основі диференціальних залежностей, бачимо, що вони відповідають всім особливостям епюр, вказаних вище.

Крім того, під точкою А на епюрах Q і М є стрибки, які дорівнюють реакціям таМ_А в жорсткому закріпленні.

Таким чином: кНм,М_А = 20 кНм.