
- •Електромагнетизм
- •1. Магнітне поле електричного струму
- •2. Сила, що діє на провідник з струмом в магнітному полі.
- •3.Сила, діюча на заряд, який рухається в магнітному полі
- •4. Закон повного струму, магнітний потік, магнітна індукція у феромагнетику
- •5. Робота переміщення провідника зі струмом у магнітному полі. Електрорушійна сила (ерс) індукції Основні формули
- •6. Самоіндукція. Екстраструми замикання і розмикання
- •7. Енергія магнітного поля
- •8. Електромагнітні коливання і хвилі
- •Контрольна робота №4 Список літератури
- •Таблиця варіантів до контрольної роботи №4
- •Необхідні постійні
5. Робота переміщення провідника зі струмом у магнітному полі. Електрорушійна сила (ерс) індукції Основні формули
Робота переміщення замкнутого контуру з струмом у магнітному полі:
![]() ,
,
де ΔФ – зміна магнітного потоку, пронизуючого поверхню, обмежену контуром; І – сила струму у контурі.
Основний закон електромагнітної індукції (закон Фарадея):
і
![]() деі
– електрорушійна сила індукції;
деі
– електрорушійна сила індукції;
N – число витків контуру; ψ – потокозчеплення.
Частинні випадки застосування основного закону електромагнітної індукції: різниця потенціалів U на кінцях провідника довжиною l, що рухається зі швидкістю V в однорідному магнітному полі:
![]() ,
де α
– кут між напрямками векторів швидкості
V
і магнітної індукції В;
,
де α
– кут між напрямками векторів швидкості
V
і магнітної індукції В;
Електрорушійна сила індукції і , виникаюча у рамці, яка має N витків, площею S, при обертанні рамки з кутовою швидкістю ω у однорідному магнітному полі з індукцією В.
і
![]() ,
деωt
– миттєве значення кута між вектором
В
і вектором нормалі n до площини рамки.
,
деωt
– миттєве значення кута між вектором
В
і вектором нормалі n до площини рамки.
Приклади розв'язування задач
Задача 1. Котушка діаметром d = 10 см має 200 витків і знаходиться у магнітному полі, індукція якого збільшується від 2 до 6Тл за 0,6с. Визначити середнє значення індукції у котушці, якщо площа витків перпендикулярна до силових ліній поля.
Розв’язання
|
Дано: d = 0,1м N = 200 витків В1 = 2Тл В2 = 6Тл ∆t = 0,1с і -? |
ЕРС індукції визначимо із закону електромагнітної індукції з урахуванням числа витків у котушці:
і
Магнітний потік
Ф, що пронизує контур:
оскільки
за умовою задачі контур перпендикулярний
силовим лініям магнітного поля, тобто
α
= 0, то
|
При зміні індукції магнітного поля змінюється і потік:
![]()
З
урахуванням того, що S
=![]() отримаємо:і
отримаємо:і
![]() .
.
Визначимо:
|і
|
![]()
[і
]![]()
Задача 2. Прямий провідник довжиною l = 40см рухається в однорідному магнітному полі з швидкістю V = 5м/с перпендикулярно до ліній індукції. ЕРС індукції між кінцями провідника 0,6В. Визначити індукцію магнітного поля.
Розв’язання
|
Дано: l = 0,4м V = 5м/с і = 0,6В |
Якщо провідник рухається у магнітному полі то у ньому виникає ЕРС індукції: і
Згідно з умовою задачі α=π/2, звідси:
|
|
α = 90о В -? |
і
Підрахуємо: |

Задача
3.
В однорідному магнітному полі з індукцією
В
= 0,02 Тл навколо осі, паралельній лініям
індукції, обертається тонкий однорідний
стержень довжиною l
= 40 см. Вісь обертання перпендикулярна
до стержня й проходить через один із
його кінців; кутова швидкість
![]() .
Знайти різницю потенціалів між віссю(точка
О) і серединою стержня(точка А)(рис. 17).
.
Знайти різницю потенціалів між віссю(точка
О) і серединою стержня(точка А)(рис. 17).
Розв’язання
|
Дано: В = 0,02 Тл l = 0,4 м
∆φ -? |
При русі стержня у магнітному полі у ньому виникає ЕРС індукції. Це зв’язано з тим, що у кожному провіднику є вільні електричні заряди і при переміщенні їх в магнітному полі на них діє сила Лоренца Fл. Дія цієї сили призводить до перерозподілу зарядів у провіднику, тобто заряди протилежних знаків накопичуються у |
р ізних
місцях стержня. Ця різниця потенціалів
між 2-ма крайніми точками стержня
ізних
місцях стержня. Ця різниця потенціалів
між 2-ма крайніми точками стержня![]() ,
,
де
Еk
– напруженість кулонівського поля
всередині стержня;
![]()
Сила
Лоренца дорівнює
![]() .
ТодіЕк
=
.
ТодіЕк
=
![]() ,
α – кут між
векторами
,
α – кут між
векторами
![]() і
і![]() .
У даному випадкуα
= π/2
(за умовою). Звідси:
.
У даному випадкуα
= π/2
(за умовою). Звідси:
![]() (1)
(1)
Якщо
стержень обертається так, як показано
на малюнку (вісь обертання проходить
через т. О), то електрони будуть
накопичуватись на закріпленому кінці
стержня в т.О) і
![]() буде негативним.
буде негативним.
Для
розрахунку введемо радіус-вектор
![]() ,
направлений від осі обертання вздовж
стержня. При інтегруванні виразу (1) від
0 до А
,
направлений від осі обертання вздовж
стержня. При інтегруванні виразу (1) від
0 до А
![]() .
Тоді
.
Тоді![]() .
АлеV
= ω·r
і при інтегруванні від 0 до А радіус-вектор
r змінюється від 0 до l/2.
.
АлеV
= ω·r
і при інтегруванні від 0 до А радіус-вектор
r змінюється від 0 до l/2.
Звідси:

Перевірка розмірностей:
![]() .
.
Задача
4. У
однорідному магнітному полі з індукцією
В
= 0,1 Тл рівномірно обертається рамка,
яка має N
= 1000 витків з частотою
![]() .
Площа S
дорівнює 150
.
Площа S
дорівнює 150![]() .
Визначити миттєве значення ЕРС індукціїі,
що відповідає куту повороту рамки в
30.
.
Визначити миттєве значення ЕРС індукціїі,
що відповідає куту повороту рамки в
30.
Розв’язання
|
Дано: В = 0,1Тл
S = 150 см2 α = 30° N = 100витків і -? |
Миттєве значення ЕРС індукції зі визначається основним законом електромагнітної індукції: і
Потокозчеплення = NФ, де N – число витків що пронизуються магнітним потоком Ф. Підставивши вираз у вираз (1), отримаємо: |
і
![]() . (2)
. (2)
При обертанні рамки магнітний потік Ф, що пронизує рамку в момент часу t, змінюється по закону Ф= ВScost, де В – магнітна індукція;
S – площа рамки; - кругова частота. Підставивши у вираз (2) вираз Ф і продиференціювавши за часом, знайдемо миттєве значення і :
|і
|
![]() . (3)
. (3)
Кругова частота звязана з частотою n обертання співвідношенням =2n.
|і
|
![]() . (4)
. (4)
Підрахуємо:
|і
|
![]()
Перевірка розмірностей:
[і
]![]()
Задача
5.Круговий
контур розташований в однорідному
магнітному полі так, що площина контуру
перпендикулярна до ліній індукції
магнітного поля. Напруженість магнітного
поля Н
=
![]() По контуру протікає струмІ
= 2А. Радіус контуру R
= 2см. Яку роботу потрібно затратити, щоб
повернути контур на 90
навколо осі, що співпадає з діаметром
контуру?
По контуру протікає струмІ
= 2А. Радіус контуру R
= 2см. Яку роботу потрібно затратити, щоб
повернути контур на 90
навколо осі, що співпадає з діаметром
контуру?
Розв’язання
|
Дано: Н
=
І = 2А R = 2см α = 90° А -? |
Робота сил магнітного поля по переміщенню контуру зі струмом визначається по формулі А = ІФ, де
Ф
= Ф2
- Ф1
– зміна магнітного потоку, що пронизує
контур. Знаючи, що Ф
= BScos( отримаємо,
що магнітний потік в початковому
положенні рамки Ф1
= ВS, оскільки
cos( |
Ф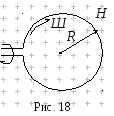 2
= 0, тому що cos(
2
= 0, тому що cos(![]() ^
^![]() )
= 0.
)
= 0.
Нарешті:
А = І(0-BS) =
-IB = -I0H![]() ,де
,де
![]() =
S.
=
S.
Робота є негативною, значить вона здійснюється проти магнітних сил(контур до повороту знаходиться в стані рівноваги). Енергія системи після такого повороту збільшується.
Робота зовнішніх сил: Азов. = -А.
Підрахунок і перевірка розмірностей:
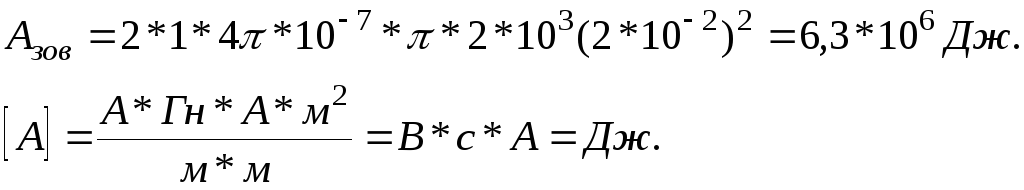
Задача
6.
Прямокутна рамка із струмом розташована
у магнітному полі так, що площина рамки
паралельна лініям магнітної індукції.
На рамку діє обертальний момент
![]() .
Визначити роботу сил поля при повороті
рамки на кут
.
Визначити роботу сил поля при повороті
рамки на кут![]() .
.
Розв’язання
|
А -?
|
|
Робота
по переміщенню контуру зі струмом у
магнітному полі: А=ІФ=І(Ф2-Ф1).
Обертальний момент, діючий у початковому
положенні на рамку
![]() ,
де
,
де![]() - магнітний момент рамки зі струмом;Ф=BScos
- магнітний момент рамки зі струмом;Ф=BScos![]() - магнітний потік через площу рамки.
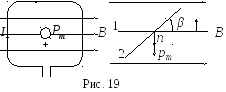
Враховуючи орієнтацію рамки в початковий
момент(див. рис. 19) отримаємо, що Ф=BScos
- магнітний потік через площу рамки.
Враховуючи орієнтацію рамки в початковий
момент(див. рис. 19) отримаємо, що Ф=BScos![]() =0,
М=ІВS.
=0,
М=ІВS.
Тоді
робота: А=
ІФ2=ІВScos![]()
Зробимо підрахунок та перевірку розмірностей:
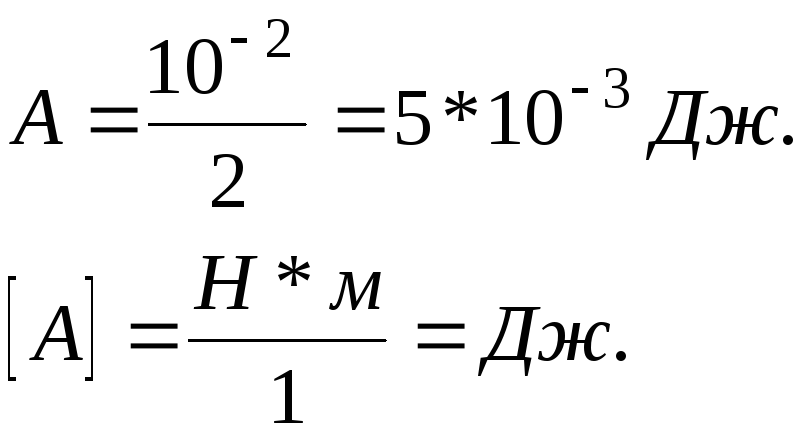

 Дано:
Дано: