
- •Електромагнетизм
- •1. Магнітне поле електричного струму
- •2. Сила, що діє на провідник з струмом в магнітному полі.
- •3.Сила, діюча на заряд, який рухається в магнітному полі
- •4. Закон повного струму, магнітний потік, магнітна індукція у феромагнетику
- •5. Робота переміщення провідника зі струмом у магнітному полі. Електрорушійна сила (ерс) індукції Основні формули
- •6. Самоіндукція. Екстраструми замикання і розмикання
- •7. Енергія магнітного поля
- •8. Електромагнітні коливання і хвилі
- •Контрольна робота №4 Список літератури
- •Таблиця варіантів до контрольної роботи №4
- •Необхідні постійні
3.Сила, діюча на заряд, який рухається в магнітному полі
Основні формули
Сила Лоренца.
Сила F, діюча на заряд, що рухається із швидкістю V в магнітному полі з індукцією В (сила Лоренца), виражається формулою
![]() .
.
Числове значення сили Лоренца дорівнює
![]() ,
де
,
де![]() - кут між векторами
- кут між векторами![]() і
і![]() .
.
Сила Лоренца завжди
направлена перпендикулярно до швидкості
руху заряду
![]() і тому відіграє роль доцентрової сили,
тобто
і тому відіграє роль доцентрової сили,
тобто
![]() ,
де
,
де![]() ,
,![]() ,m
– маса частинки, R
– радіус кривизни траєкторії частинки.
Сила Лоренца не виконує роботу, так як
вона змінює тільки напрям швидкості
заряду в магнітному полі
,m
– маса частинки, R
– радіус кривизни траєкторії частинки.
Сила Лоренца не виконує роботу, так як
вона змінює тільки напрям швидкості
заряду в магнітному полі
![]() ;
бо
;
бо
![]()
Період обертання T частинки в магнітному полі дорівнює
T=![]() .
.
Рух заряджених частинок в суміщених магнітному та електричному полях.
В загальному
випадку на електричний заряд, що
рухається, крім магнітного поля з
індукцією В, може ще діяти і електричне
поле з напруженістю Е. В цьому випадку
сила Лоренца буде дорівнювати векторній
сумі електричної сили
![]() та сили Лоренца
та сили Лоренца![]() .
.
Зміна маси частинки від її швидкості
 ,
де
,
де
 =
= ;
;
![]() -
швидкість світла у вакуумі.
-
швидкість світла у вакуумі.
Релятивістський імпульс P=
 ,
,
де m0 – маса спокою частинки.
Приклади розв’язування задач
Задача 1.
Електрон, пройшовши прискорюючу різницю
потенціалів U
= 400 B, потрапив в однорідне магнітне поле
напруженістю H
= 1000 А/м. Визначити радіус кривизни
траєкторії і частоту обертання електрона
в магнітному полі. Вектор швидкості
перпендикулярний до ліній напруженості
магнітного поля. Маса електрона mе
=
![]() ,
його заряд
,
його заряд![]() .
.
Розв’язання
|
Дано: U = 400 D H = 1000 А/м mе
=
R -? ν -? |
На заряд q,
що рухається в магнітному полі Н,
діє сила Лоренца (рис. 12). Ця сила
відіграє роль доцентрової сили, так
як змінює напрям швидкості без зміни
її значення, тобто
Силу Лоренца можна визначити по формулі
|
З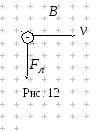 а
умовою
а
умовою![]() ,
так як в магнітному полі рухається
електрон
,
так як в магнітному полі рухається
електрон![]() ,
а
,
а![]()
З
іншого боку, відцентрова сила
![]() .
.
Враховуючи
(1), отримаємо
![]() .
Звідки
.
Звідки
![]() .
(2)
.
(2)
Аналізуючи формулу(2), відмічаємо, що для визначення радіуса траєкторії r необхідно знати швидкість v частинки і індукцію магнітного поля В, яку слід виразити через напруженість Н:
![]() .
(3)
.
(3)
Швидкість електрона можна визначити, знаючи прискорюючу різницю потенціалів; електрон набуває кінетичної енергію, з якою він влітає в магнітне поле за рахунок роботи сил електричного поля:
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Звідки
![]() .
(4)
.
(4)
Підставивши (3) і
(4) в (2), отримаємо
 ,
де
,
де![]() - магнітна постійна,
- магнітна постійна,![]() - магнітна проникність повітря.
- магнітна проникність повітря.
Виконаємо підрахунки і перевірку розмірностей:
![]() м.=5.4 см;
м.=5.4 см;
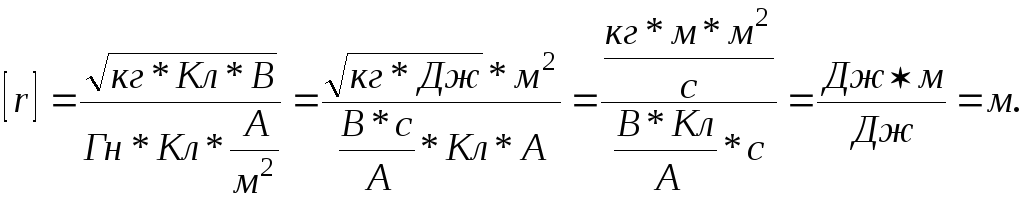
Період
обертання Т
електрона по орбіті дорівнює часу одного
оберт. Шлях одного оберту дорівнює
довжині кола S=2r,
тоді:![]()
Частота
обертання ν
1/T,
тоді:

Виконаємо підрахунки і перевірку розмірностей:
![]()

Задача
2.
Перпендикулярно до однорідного
електричного поля з напруженістю Е
=
800
В/м збуджено
однорідне магнітне поле з напруженістю
![]() м.
Пучок електронів, що рухаються
перпендикулярно до силових ліній обох
полів, не має ніяких відхилень. Знайти
швидкість електронів у пучку.
м.
Пучок електронів, що рухаються
перпендикулярно до силових ліній обох
полів, не має ніяких відхилень. Знайти
швидкість електронів у пучку.
Розв’язання
|
V - ? |
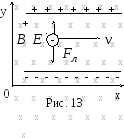
На
електрони які рухаються у схрещених
електричному і магнітному полях діють
одночасно дві сили: зі сторони
електричного поля
отримуємо:
Виконаємо підрахунки і перевірку розмірностей:
|
Задача
3.
Протон влітає в однорідне магнітне поле
з індукцією В
= 0,1 Тл, під кутом
![]() до напряму поля і рухається по спіралі,
радіусом r
= 1.5 см. Знайти кінетичну енергію протона.
до напряму поля і рухається по спіралі,
радіусом r
= 1.5 см. Знайти кінетичну енергію протона.
Розв’язання
|
Дано:
|
Кінетична
енергія протона (при v<<c)
знаходиться за повною його швидкістю: Радіус спіралі, по якій рухається протон |
|
|
визначається силою Лоренца:
де Vn= Vsin- складова швидкості протона, перпендикулярна до вектора індукції магнітного |
п оля.
Звідси:
оля.
Звідси:![]() ,
тоді швидкість протона
,
тоді швидкість протона![]() а шукана кінетична енергія:
а шукана кінетична енергія:
![]() Виконаємо
підрахунки і перевірку розмірностей:
Виконаємо
підрахунки і перевірку розмірностей:

Задача 4. Електрон рухається в однорідному магнітному полі з індукцією В = 0,03 Тл., по колу з радіусом r = 10 см. Визначити швидкість електрона.
Розв’язання
|
Дано: В = 0,03 Тл r = 10 см v - ? |
Рух електрона по колу в однорідному магнітному полі здійснюється під дією сили Лоренца. Отже, можна сказати, що:
|
звідси знаходимо імпульс електрона:
![]() (2)
(2)
релятивістський імпульс виражається формулою:
![]() .
.
Виконавши перетворення, отримуємо наступну формулу для визначення швидкості частинок:
![]() (3)
(3)
В даному випадку p=|e|Br. Звідси:
![]() (4)
(4)
У
чисельник і знаменник формули (4) входить
вираз
![]() .
Знайдемо його окремо:
.
Знайдемо його окремо:
![]() =
=![]()
Підставивши знайдене значення у формулу (4), отримаємо:
![]() .
.
Електрон, який має таку швидкість, є релятивістським.

 Дано:
Дано: