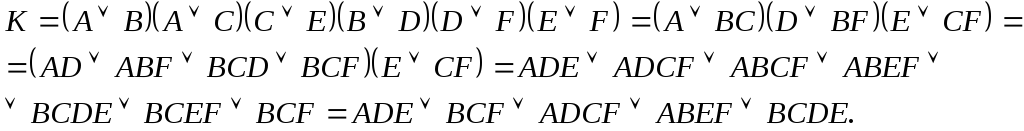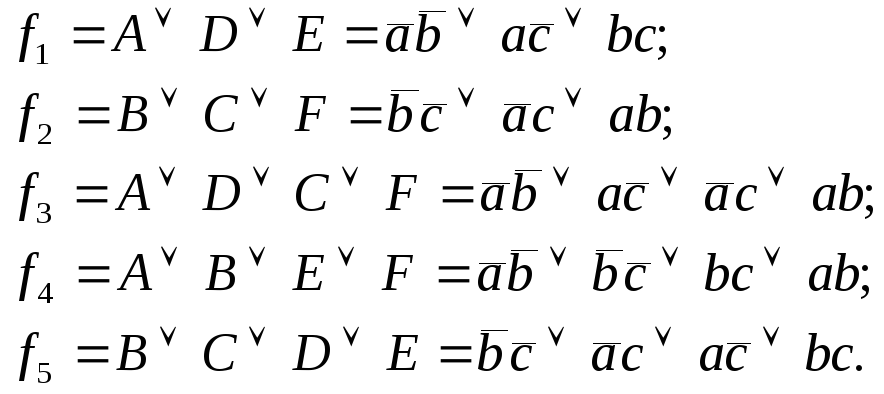Шпоры / шпоры / Шпорки3

13. Конъюнктивная нормальная форма логических функций и методы ее получения. СКНФ. Получение СКНФ из таблицы соответсвия. Переход от СКНФ к запрещенным наборам.

Если логическая функция, зависящая от n переменных, записана в виде конъюнкции элементарных дизъюнкций, каждая из которых не обязательно включает в себя все n переменных, то такая форма записи называется конъюнктивной нормальной формой (КНФ). Иначе говоря, конъюнктивной нормальной формой логической функции называется конъюнкция любого конечного множества попарно различных элементарных дизъюнкций. Например:

Произвольная логическая функция, заданная аналитическим выражением, может быть приведена к КНФ. Для этого необходимо:

-заданную функцию проинверсировать и получить ДНФ инверсной функции;

-ДНФ инверсной функции проинверсировать еще раз;

-на каждом этапе следует проводить все упрощения согласно законам алгебры логики (закон повторения, закон поглощения и т.д.). В результате получим КНФ исходной функции. Для того чтобы от СКНФ перейти к запрещенным наборам (т.е. совокупностям значений переменных, при которых функция равна 0), необходимо в каждой элементарной дизъюнкции расположить переменные в определенном порядке (выбрать базу) и, заменив символы переменных с инверсией на 1, а без инверсии на 0, записать вместо элементарных дизъюнкций совокупность двоичных чисел. То есть – взять инверсии элементарных дизъюнкций. Десятичное (восьмеричное) представление этих чисел есть запрещенные числа для данной функции.

Если никаких дополнительных указаний нет, то все остальные числа из области задания функции считаются рабочими.

14. Задачи и сущность минимизации логических функций. Импликанты. Сокращенная, тупиковая, минимальные дизъюнктивные нормальные формы

Сущность минимизации логической функции, заданной в СДНФ, заключается в том, что получают ДНФ заданной функции путем группировки соседних, отличающихся друг от друга значением только одной переменной членов (конституент) СДНФ и исключением одной переменной по соотношению (по закону склеивания). Описанная операция носит название склеивания. После нее производят упрощения по закону повторения. Этот процесс попарного склеивания повторяют до тех пор, пока в полученном выражении не останется конъюнкций, отличающихся значением одной переменной. Получают минимизированную логическую функцию. Однако такая минимизация СДНФ методом непосредственного упрощения, т.е. попарного склеивания, является чрезвычайно громоздкой операцией и для сложных функций вообще не приемлема.

Логическая функция называется импликантой логической функции если на любом наборе значений переменных на котором значение функции равно 1, значение функции также равно 1. Простой импликантой функции f(x) называется элементарная конъюнкция g(x), являющаяся импликантой этой функции и обладающая тем свойством, что никакая ее собственная часть, т.е. конъюнкция, получаемая из элементарной путем исключения одной или нескольких переменных, уже не является импликантой данной функции. Дизъюнкция всех простых импликант логической функции называется сокращенной дизъюнктивной нормальной формой этой функции (СкДНФ). Дизъюнкция простых импликант, составляющих приведенную систему импликант функции, называется ее тупиковой дизъюнктивной нормальной формой (ТДНФ). Отметим, что полученная в примере единственная ТДНФ, очевидно, является и МДНФ. Минимальная ДНФ функции, найденная путем построения и перебора всех тупиковых ДНФ и выбора из них самой минимальной, называется общей (абсолютной) минимальной ДНФ. При решении практических задач часто затруднительно отыскать все тупиковые ДНФ логической функции. Поэтому, чтобы сократить объем работы, ограничиваются нахождением одной или нескольких ТДНФ, из которых выбирают минимальную. Такие минимальные ДНФ называются частными дизъюнктивными нормальными формами. Получив частную минимальную ДНФ (одну из ТДНФ), считают ее близкой к общей МДНФ, что, вообще говоря, не всегда является верным. Особенно большое отличие по количеству букв частных МДНФ (ТДНФ) от общей МДНФ наблюдается при решении задач синтеза ДУ по не полностью определенным логическим функциям, которые в процессе минимизации доопределяются за счет условных наборов переменных. Поэтому следует выбирать такой способ доопределения, который ведет к получению наиболее близкой к минимальной ТДНФ.

15. Таблично-аналитический метод минимизации логических функций - метод Квайна-Мак-Класски.

Существует несколько методов нахождения импликант и построения минимальной ДНФ. Одним из них является метод попарного сравнения всех конституент, входящих в функцию, так называемый метод Квайна – Мак-Класки. Рассмотрим его. Первым этапом минимизации является построение сокращенной ДНФ, для чего нужно определить все простые импликанты заданной функции путем сравнения каждой конституенты СДНФ попарно со всеми последующими и выполнения операции склеивания. После этого шага производят аналогичную операцию с полученными импликантами и т.д. до тех пор, пока оставшиеся импликанты больше не будут поддаваться склеиванию. Это и есть простые импликанты, их дизъюнкция представляет собой СкДНФ функции. Для некоторого сокращения количества сравнений рекомендуется все конституенты записать в столбик и разбить на группы по числу неинверсированных переменных. В этом случае каждая очередная конституента, начиная сверху, сравнивается только с конституентами группы, соседней снизу, с числом неинверсированных переменных на единицу больше. Результат попарного склеивания выписывается справа в новый столбик. После окончания склеивания в первом столбце переходят к склеиванию во втором столбце и т.д. Выражения, вошедшие хотя бы в одно склеивание, отмечаются звездочками. После окончания процедуры склеивания члены, не отмеченные звездочками, и будут простыми импликантами

16. Карты Карно. Задание логической функции картой Карно. Свойство карты Карно. Цифровая кодировка карты Карно.

При решении задач минимизации логических функций, зависящих от небольшого числа переменных, находят широкое применение графические методы. Наиболее применимы эти методы для минимизации логических функций четырех переменных, однако при соответствующем навыке их можно применять и для функций пяти-шести переменных. При большем числе переменных эти методы теряют свое основное достоинство – наглядность и становятся неэффективными. Наибольшее распространение получил метод минимизации с помощью карт Карно. Карта Карно – это диаграмма, в которой каждому возможному набору переменных функции поставлена в соответствие одна клетка. Клеток должно быть, как и наборов, 2ⁿ. В каждую клетку записывается значение функции (0 или 1) для данного набора. Входные переменные располагаются по внешним сторонам карты напротив ее строк и столбцов. При этом значение каждой из входных переменных относится ко всей строке (или столбцу) и равно 1, если напротив строки (или столбца) стоит под скобкой обозначение этой переменной; для остальных строк (столбцов) значение этой переменной равно 0. Эти значения входных переменных не пишутся на карте, а подразумеваются. Каждая клетка карты соответствует определенному набору переменных. Этот набор образует код клетки. Каждая из входных переменных делит карту Карно на две равные части, в одной из которых значение этой переменной равно 1, а в другой 0.Каждой клетке карты Карно соответствует один определенный набор, а каждая сторона клетки представляет собой границу между значениями переменных. Чтобы составить карту Карно для функции, заданной таблицей соответствия, необходимо построить карту с числом клеток, равным числу строк таблицы; по внешним сторонам карты определенным образом расположить входные переменные. Для каждого набора (строки) таблицы отыскать соответствующий набор (клетку) карты. В эту клетку проставить значение функции для данного набора.

17. Минимизация логических функций по картам Карно. Простые импликанты. Максимальные правильные контуры. Методика минимизации

Метод минимизации логических функций по картам Карно в инженерной практике применяется большей частью для минимизации не полностью определенных логических функций, зависящих не более чем от четырех переменных и заданных в СДНФ или в символической форме. Методика минимизации логических функций по картам Карно заключается в следующем:

1.Построить карту Карно для заданной функции по числу ее переменных и отметить на ней все единичные, нулевые и условные клетки. При задании функции в СДНФ запрещенные и (или) условные наборы должны быть заданы.

2.По карте Карно, добавляя в необходимых случаях к рабочим клеткам условные, найти такую совокупность максимальных правильных контуров, чтобы каждый контур этой совокупности охватывал хотя бы одну клетку, содержащую единицу и не охваченную другими контурами, а совокупность контуров была полной, т.е. охватывала бы все единичные клетки карты Карно. При этом следует иметь в виду, что одна и та же рабочая или условная клетка может использоваться неоднократно в различных максимальных контурах, важно только, чтобы каждый контур содержал хотя бы одну единичную клетку, не вошедшую в другие контуры. Необходимо также следить, чтобы ни одна нулевая клетка не попала в выбранные контуры.

3.Для всех максимальных правильных контуров, вошедших в найденную совокупность, выписать соответствующие им простые импликанты и объединить их знаком дизъюнкции. В результате получим одну из тупиковых ДНФ, которую и принимаем за частную минимальную ДНФ.

Нетрудно установить признаки контуров карты Карно, соответствующих простой импликанте логической функции. Простой импликанте логической функции соответствует максимально возможный правильный контур, охватывающий единичные или условные клетки карты Карно. Отличительным признаком максимально возможного правильного контура является то, что он не может быть составной частью другого правильного контура. Чтобы с помощью карты Карно решать задачи минимизации логических функций, необходимо знать и уметь реализовать типичные конфигурации максимальных правильных контуров.

18. Решетка соседних чисел и обобщенных кодов. Соседние числа, обобщенные коды и их свойства. Построение и возможности решетки

Одним из инженерных методов минимизации логических функций, с помощью которого определяется одна из тупиковых ДНФ, принимаемая за частную минимальную ДНФ, является метод использования решетки соседних чисел и обобщенных кодов (метод Л. Т. Мавренкова). Рассмотрим построение и возможности решетки соседних чисел и обобщенных кодов (ОК). Известно, что логическая функция может быть задана в символической форме – в виде совокупности рабочих и запрещенных весовых состояний, представляющих десятичный (восьмеричный) эквивалент двоичных чисел, описывающих наборы переменных, на которых функция равна соответственно единице и нулю. Любую элементарную конъюнкцию (член СДНФ) можно записать двоичным числом при выбранной базе. Таким образом, логическая функция, представленная в СДНФ, может быть записана в виде логической суммы двоичных чисел. Соседние числа обладают следующими свойствами:

1.Количество чисел, соседних с данным двоичным числом, равно количеству его разрядов. Чтобы получить все числа, соседние с данным числом, необходимо, идя от старшего разряда к младшему (или наоборот), поразрядно менять 0 на 1, а 1 на 0. Например, имеем число 10 → 1010. Соседними с ним являются 0010, 1110, 1000, 1011. Отобразим это в виде диаграммы, на которой соседние числа обозначим в десятичной системе счисления в кружочках.

2.Логическая сумма двух соседних чисел приводит к исключению одной переменной (одного разряда). Например, сумму можно записать (при базе abcd) как , где вместо исключенного разряда ставится «–» (тире). Заметим, что исключается именно тот разряд, в котором соседние двоичные числа отличаются. Вместо него и ставится тире. Числовая запись конъюнкции двоичных переменных, при которой в разрядах, соответствующих нормальным переменным, поставлены 1, в разрядах, соответствующих инверсным переменным, – 0, а в разрядах, в которых отсутствуют переменные, – «–», называется обобщенным кодом. Упрощенно говоря, обобщенный код – это выражение, состоящее из единиц, нулей и тире. Свойства обобщенных кодов (ОК):

1.Количество обобщенных кодов, соседних данному, равно числу нулей и единиц в данном обобщенном коде. Соседние ОК определяются так же, как и соседние числа. Например, для ОК 11 – 0 соседними являются 01 – 0, 10 – 0, 11 – 1.

2.Логическая сумма двух соседних ОК равна ОК, содержащему тире в том разряде, в котором записанные коды были противоположны, и совпадающему с ними в остальных разрядах. Например: Обобщенный код, имеющий тире в t разрядах, равен логической сумме 2^T двоичных чисел, содержащих все комбинации 0 и 1 в этих разрядах и совпадающих с обобщенным кодом в остальных разрядах. Например, , т.е. вместо каждого тире делаем перебор 0 и 1