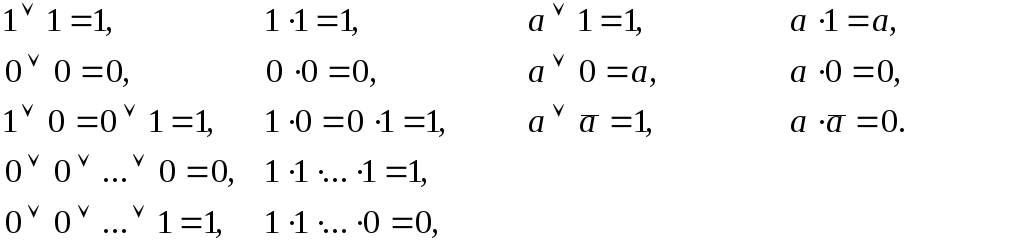Шпоры / шпоры / Шпорки2

7. Элементарные логические функции. Функции одной переменной. Основные функции двух переменных.

С увеличением числа переменных число различных логических функций очень быстро растет, и изучить все их особенности невозможно. Однако нетрудно показать, что любую функцию, зависящую от n переменных (n > 2), можно выразить через функции, зависящие от одной или двух переменных. Поэтому логические функции, зависящие от одной или двух переменных, занимают особое место в алгебре логики. Их называют элементарными логическими функциями. Рассмотрим их кратко. Их всего . Две из них – и – не зависят от x. Они называются соответственно нулевой функцией – константой 0 и единичной функцией – константой 1. Другие две повторение и инверсия. Логических функций от двух переменных всего Шесть из них являются вырожденными функциями, зависящими от одной переменной:

Остальные десять функций зависят от двух переменных.

8. Метод суперпозиции логических функций. Функционально полные наборы логических функций. Логические элементы, реализующие основные логические функции.

Система элементарных логических функций называется функционально полной, если любая логическая функция может быть представлена в виде суперпозиции функций этой системы. Функционально полная система логических функций называется минимальной, если удаление из нее хотя бы одной функции превращает систему в неполную. Критерий полноты системы функций алгебры логики устанавливает теорема Поста-Яблонского, по которой для полноты системы логических функций необходимо и достаточно, чтобы она содержала следующие функции: не сохраняющую константу «нуль», не сохраняющую константу «единица», не являющуюся самодвойственной, не являющуюся линейной, не являющуюся монотонной, т.е. каждое из перечисленных выше свойств не принадлежало бы какой-либо из функций в этой системе. Наибольшее распространение в теории и практике дискретных устройств, особенно с точки зрения технической реализации, получили функционально полные системы, состоящие из двух функций: функции И и НЕ; функции ИЛИ и НЕ; состоящие из одной функции: функции И-НЕ; функции ИЛИ-НЕ и состоящие из трех функций: функции И, ИЛИ, НЕ. Последняя полная система функций не является минимальной, но зачастую весьма удобная для представления сложных функций. Она иногда называется «основной».

Логические элементы: повторитель, инвертор (НЕ), дизъюнктор (ИЛИ), коньюнктор (И), И-НЕ, ИЛИ-НЕ.

9. Соотношения "0" и "1" в алгебре логики. Порядок инверсирования логических функций.

Кроме перечисленных законов большое значение в алгебре логики имеют так называемые соотношения 0 и 1. Напомним, что в алгебре логики символом 1 обозначается всегда истинное суждение (есть сигнал), а символом 0 – всегда ложное суждение (нет сигнала). На основании алгебры логики очевидны следующие соотношения (аксиомы алгебры логики):

Последние соотношения (относительно a) легко доказываются подстановкой вместо a его возможных значений – 0 и 1. Рассмотренные законы применимы не только к отдельным переменным, но и к группам переменных, объединенных операциями алгебры логики. В алгебре логики установлен порядок выполнения действий. При отсутствии в выражении скобок первыми должны выполняться операции отрицания (инверсии), затем операции конъюнкции и последними – операции дизъюнкции. При наличии в выражении скобок в первую очередь производятся операции внутри скобок. При преобразовании логических функций зачастую приходится производить операцию инверсирования их. Логическая функция «не f» будет инверсной по отношению к функции f, если соблюдаются два соотношения:

Следовательно, если на каком-либо наборе переменных функция f принимает значение 0, то функция «не f» равняется 1 и наоборот. Для контактных схем это означает, что если при данном состоянии реле цепь, соответствующая f, замкнута, то цепь, соответствующая «не f» – разомкнута и наоборот. Под инверсированием (логическим отрицанием) функции f понимается нахождение функции «не f», удовлетворяющей указанным соотношениям. На основании законов инверсии можно сформулировать следующий порядок инверсирования булевых функций, записанных в базисе И, ИЛИ, НЕ. При инверсировании булевой функции все знаки дизъюнкции заменяются на знаки конъюнкции и наоборот – при одновременном инверсировании каждого элемента. При этом для сохранения последовательности действий необходимо соответствующим образом вводить или исключать скобки. Другими словами, логическое инверсирование производится на основе закона инверсии, который последовательно применяется к отдельным частям функции в порядке, указанном логическими операциями и определяемом самой функцией. Например, дана функция Найти Очевидно, F – конъюнкция a и Значит, первым применяем закон инверсии относительно умножения, далее– относительно сложения во второй части и т.д.:

10. Основные законы алгебры логики.

Основные законы алгебры логики являются двойственными: относительно логического сложения и относительно логического умножения. Ими являются:

1.Переместительный (коммутативный) закон:

-относительно сложения

-относительно умножения

2.Сочетательный (ассоциативный) закон:

-относительно сложения

-относительно умножения

3.Распределительный (дистрибутивный) закон:

-относительно сложения

-относительно умножения

4.Закон инверсии (де Моргана):

-относительно сложения

-относительно умножения

5.Закон повторения (идемпотентности):

Дополнительные законы:

1.Закон поглощения:

2.Закон склеивания:

3.Закон обобщенного склеивания:

11. Основные формулы равносильных преобразований (с примерами).

Рассмотренные законы алгебры логики и соотношения 0 и1 позволяют производить равносильные преобразования логических функций, т.е. получать из исходных функций более простые, содержащие меньшее число переменных, и равносильные по своему действию исходным. Преобразование логических функций используется при анализе, синтезе и логическом контроле ДУ. Мощным аппаратом для равносильных преобразований являются так называемые основные формулы равносильных преобразований.

Относительно умножения:

Символом ~ над переменной обозначаем, что имеется в виду и нормальная, и инверсная переменные:

Из формул видно, что если переменная логически умножается на функцию f, то в этой функции все одноименные переменные заменяются на 1, а все инверсные – на 0.

П р и м е р ы:

Приведенные формулы можно заменить одной:

Относительно сложения:

Если переменная логически складывается с функцией f, то в этой функции все одноименные переменные заменяются на 0, а все инверсные – на 1.

Эти формулы можно заменить одной:

Основные формулы равносильных преобразований доказываются методом подстановки в них вместо переменной x ее возможных значений 0 и 1 и сравнения правой и левой частей уравнения.

Рассмотрим некоторые примеры.

1.Упростить логическую функцию

Применяем законы алгебры логики (2 раза распределительный закон) и получаем:

12. Дизъюнктивная нормальная форма логических функций и методы ее получения. СДНФ. Переход от СДНФ к рабочим наборам. Получение СДНФ из таблицы соответствия.

Дизъюнктивной нормальной формой логической функции называется дизъюнкция любого конечного множества попарно различных элементарных конъюнкций. Например:

Произвольная логическая функция всегда может быть приведена к ДНФ.

Методика приведения логической функции к ДНФ следующая:

-выполнить все операции инверсии, применяемые к логическим выражениям (группе переменных); -раскрыть все скобки; в полученных конъюнкциях произвести все упрощения согласно законам и соотношениям алгебры логики (исключение конъюнкций, равных нулю, применение закона повторения и т.д.). Для того чтобы от СДНФ перейти к рабочим наборам, необходимо расположить в каждой конъюнкции переменные в определенном одинаковом порядке (выбрать базу) и заменить символы переменных с инверсией на 0, а без инверсии – на 1. Считая веса двоичных разрядов возрастающими от 2⁰ справа налево, можно без труда определить рабочие числа и записать функцию в символической форме. При этом, если никаких дополнительных указаний нет, то все остальные числа из области задания функции считаются запрещенными.