Шпоры / шпоры тау / 2006дистанционники / Lekcii / Lekcija №27
.DOC
Разностные уравнения
Аналогом первой производной непрерывной функции для решетчатой функции является либо первая обратная разность
f[n] = f[n] - f[n-1],
либо первая прямая разность
f[n] = f[n+1] - f[n].
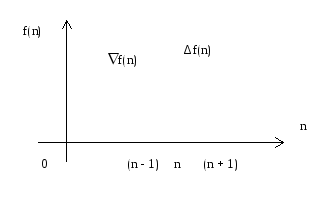Прямая
разность определяется в момент времени
t=nT по
будущему значению решетчатой функции
при t=(n+1)*Т.
Это можно сделать в тех случаях, когда
будущее значение известно.
Обратная разность определяется для момента времени t=nT по прошлому значению решетчатой функции в момент времени (n - 1)*Т.
Аналогом второй производной служат вторые разности:
Обратная
.
Для вычисления k-й разности используют рекуррентную формулу
или формулу общего вида
, (1)
где биномиальные
коэффициенты (число сочетаний)
.
Обратные разности обладают важной особенностью: если решетчатая функция определена только для положительных значений аргумента, то есть
при n<0,
то в точке n=0 k-я
разность
для любого целого положительного k.
Аналогами интегралов непрерывных функций в пределах от 0 до t для решетчатых функций являются неполные суммы
и полные суммы
.
В качестве аналогов дифференциальных уравнений рассматриваются уравнения в конечных разностях.
При использовании обратных разностей уравнение в конечных разностях будет иметь вид
.
С учетом формулы (1) последнее выражение приобретает вид
,
коэффициенты уравнения определяются выражениями
,
.
Общее решение
однородного разностного уравнения при
некратных корнях характеристического
уравнения может быть записано следующим
образом:
,
(2)
где
(i=1,2,…,m)
– корни характеристического уравнения
,
а
- произвольные постоянные.
Из (2) вытекает
условие того, чтобы свободное движение
системы, описываемой разностным
уравнением, было бы затухающим (условие
устойчивости): |
|<1 (i=1,2,…,m).
Для исследования решений разностных уравнений используются дискретное преобразование Лапласа, z – преобразование, w – преобразование, а также частотные методы.
Дискретное преобразование Лапласа
Для решетчатых функций введено понятие дискретного преобразования Лапласа в соответствии с формулой
. (3)
Для смещенных решетчатых функций может быть записано аналогичное выражение:
. (4)
В приведенных формулах, как и в случае непрерывного преобразования Лапласа, комплексная величина p=c+jω, где с – абсцисса абсолютной сходимости. Если с, то ряд, определяемый формулами (3,4), сходится и решетчатой функции соответствует некоторое изображение.
Z–преобразование
Z–преобразование
вытекает из дискретного преобразования
Лапласа путем введения новой переменной
.
Z–преобразование есть изображение несмещенной или смещенной решетчатых функций, определяемое формулами
,
.
Если для данной
решетчатой функции f[n]
существует такое положительное число
R, что при |z|>R
ряд
(5)
сходится, то =1/R называют радиусом сходимости.
Функция
внутри круга сходимости (т.е. круга в
плоскости z с центром в
начале координат и радиусом равным )
будет аналитической функцией, а ряд (5)
будет рядом Лорана. Коэффициенты ряда
f[nT] выражаются
через
следующим образом:
.
Формулы преобразования могут быть записаны и для непрерывной производящей функции в виде
F(z)=Z{f(t)}, t=nT, n=0,1,2… .
В рассматриваемом
пространстве введена единичная импульсная
решетчатая функция
Эта функция играет в дискретных системах такую же важную роль, как - функция (функция Дирака) в непрерывных системах.
Основные свойства и теоремы Z-преобразования
-
Свойство линейности.
Изображение линейной комбинации решетчатых функций равно той же линейной комбинации их изображений.
.
-
Теорема запаздывания.
Рассмотрим решетчатую функцию f[n-m], сдвинутую вправо (запаздывающую) на целое число тактов m. Если обозначить n-m=r, то
Z{f[n-m]}=
=
=
.
Если исходная
решетчатая функция f[n]
равна нулю при отрицательных значениях
аргумента, то z{f[n-m]}=
.
-
Изображение разностей.
Для первой обратной разности
.
Если для отрицательных
аргументов решетчатая функция тождественно
равно нулю, то
.
Для k-й обратной разности при f[n]0 для n<0
,
.
Определение обратной разности и полной суммы (или прямой разности и неполной суммы) решетчатой функции являются обратными операциями. Роль оператора, аналогичного оператору p=c+jω в непрерывных системах, в первом случае играет оператор (z-1)z-1, а во втором случае – оператор (z-1). В случае перехода к пределу при T0 обе пары операций над решетчатыми функциями сливаются и превращаются в операции дифференцирования и интегрирования непрерывной функции.
-
Конечное значение решетчатой функции.
Если объект (система) устойчивы и предел существует, т.е. если все полюсы (z-1)F(z) находятся внутри единичной окружности |z|=1 на z-плоскости, то
.
Пример. Конечное
значение единичной функции
определяется следующим образом:
.
-
Начальное значение решетчатой функции.
Если предел существует, то
.
Пример.
.
-
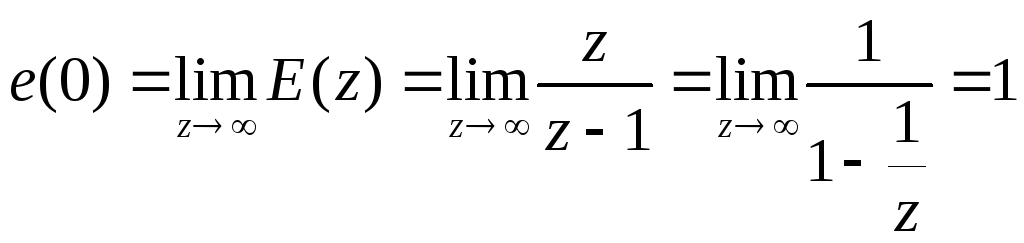Разложение в ряд Лорана (ряд по убывающим степеням z).
.
Разложив любым способом изображение F(z) в ряд Лорана:
,
и, сравнивая два ряда между собой, можно
установить, что
,
,
,…,
и т.д.
-
Решение разностных уравнений.
Более удобны для решения разностные уравнения вида
с начальными
условиями
,
.
Изображение
решетчатой функции y[n-m],
запаздывающей на m тактов,
будет 
.
Подобные зависимости могут быть записаны для запаздывания на (m-1), (m-2),…, 1 тактов.
В случае нулевых
начальных условий
.
Если предположить, что решетчатая функция y[n] тождественно равна нулю при n < 0 и, кроме того, функция f[n] в правой части прикладывается в момент времени n=0, то переход к изображениям дает
.
Изображение искомой решетчатой функции можно представить в виде
,
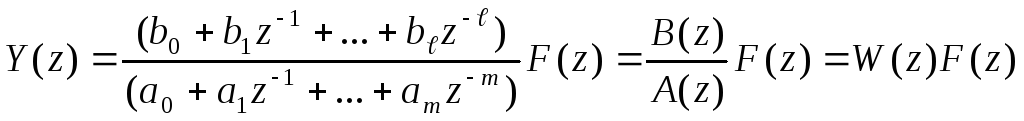где W(z) - дискретная передаточная функция.
Пример 1. Определить z - изображение единичной ступенчатой решетчатой функции f[nT] при T=1c.
1(t) – производящая функция;
L1(t)=
.
;
;
.
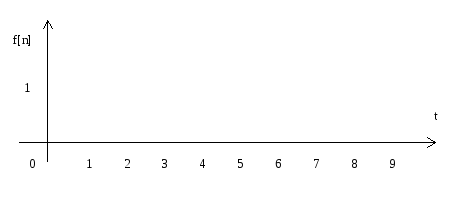Используем
формулу суммирования убывающей
геометрической прогрессии 
.
Для бесконечно убывающей прогрессии n,
тогда
.
Знаменатель прогрессии q=z-1.
Тогда для |z|>1 
.
Пример
2. Задана решетчатая экспонента
,
где - постоянная,
в общем случае, комплексная величина,
T=1c.
;
;
;
;
знаменатель
прогрессии q=z-1
.
Для |z| > e-αT
,
где d=e-αT.
|
NN n. n. |
w(t) |
w(nT) |
W(p) |
W(z) |
|
1 2 . . . |
K(t) k1(t) . . . |
k k1(nT) . . . |
k k/p . . . |
k kz/(z-1) . . . |