Шпоры / шпоры тау / 2006дистанционники / Lekcii / Lekcija №32

Нелинейные САУ

Нелинейной называется такая система, для которой не применим принцип суперпозиции из-за наличия в дифференциальном уравнении степеней, тригонометрических функций, произведений переменных, звеньев с нелинейными характеристиками и т.п.

Реальные САУ нелинейны. Нелинейности подразделяют на линеаризуемые (несущественные) и нелинеаризуемые (существенные). Использование аппарата линейной теории для целей анализа и синтеза систем автоматического управления следует считать целесообразным, если при этом не допускается принципиальных качественных ошибок, а также если количественные погрешности не выходят за рамки допустимых пределов.

Нелинейным автоматическим системам присущи принципиально новые свойства в динамике, которые отсутствуют у линейных:

1. К нелинейным системам не применим принцип суперпозиции;

2. Устойчивость и качество переходных процессов в нелинейных системах зависят от степени возмущения и начальных условий;

3. Возможность возникновения в них автоколебаний (предельных циклов) в общем случае несинусоидальных, амплитуда которых не зависит от внешних воздействий и начальных условий;

4. Частота вынужденных колебаний на выходе системы может быть либо субгармоникой, либо гармоникой входного периодического сигнала;

5. Явление скачкообразного резонанса;

6. Множество состояний равновесия.

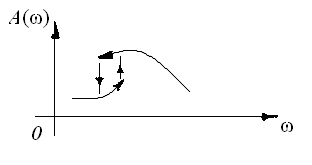
В нелинейных системах следует исследовать не устойчивость вообще, а устойчивость определённого их режима.

Чтобы судить о свойствах нелинейных систем, кроме математических и физических характеристик элементов необходимо знать вид и величины входных воздействий и область начальных условий.

Появление нелинейности в системе с линейной структурой обычно приводит к снижению качества работы последней.

Широкий класс нелинейных систем отображается в структурную схему с одной нелинейностью:

u

Виды нелинейности:

1. Звено с релейной характеристикой. Описать линейной зависимостью элемент с такой рабочей характеристикой невозможно, так как в рабочей точке имеется разрыв.

Уравнение элемента:

F(ε)=

2. Звено с релейной характеристикой и зоной нечувствительности.

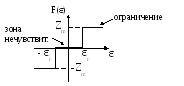Уравнение звена имеет вид

3. Звено с характеристикой типа «ограничение (насыщение)».

Необходимость исследования поведения системы «в большом» заставляет рассматривать характеристики элементов при больших значениях входных воздействий. В этом случае элемент может оказаться нелинейным, хотя и является линеаризуемым «в малом».

ε

Z

-Z_m

Z_m

α

ε_r

-ε_r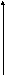

Уравнение элемента:

-Z_m при ε ≤ ε_r ,

ε · tg α при | ε | ≤ ε_r ,

Z_m при ε ≥ ε_r , причём Z_m= ε_r· tg α.

Устойчивость нелинейных систем

Нелинейные системы в отличие от линейных могут быть устойчивы в одних режимах работы и неустойчивы в других.

Различают устойчивость в малом, в большом, в целом.

Движение устойчиво в малом, если условия устойчивости выполняются лишь в малой окрестности равновесия, то есть при малых начальных отклонениях.

Если же движение устойчиво при конечных отклонениях, возможных в данной системе по условиям её работы, то его принято называть устойчивым в большом.

Движение устойчиво в целом, если оно устойчиво при любых начальных отклонениях, то есть не зависит от них.

Критерий абсолютной устойчивости В.М. Попова

Рассматривается замкнутая система с одним нелинейным звеном.

Система называется асимптотически устойчивой, если при ненулевых ограниченных начальных условиях свободное движение y(t) ограничено при t є [0,∞) и lim y(t)=0 (t→∞).

Если окажется, что это свойство выполняется для любых нелинейных элементов из некоторого класса, то устойчивость называется абсолютной.

Теорема В.М. Попова.

Пусть выполняются условия:

1. все полюсы передаточной функции линейной части системы имеют отрицательные действительные части;

2. характеристика нелинейного элемента принадлежит сектору [0,k],

т.е. F(0)=0, 0 ≤ F(ε) / ε ≤ k при всех ε≠0;

3) существует действительное число q такое, что при всех ω є [0,∞)

выполняется неравенство

Re [(1+jωq)W(jω)]+1/k = u(ω)-qωυ(ω)+1/k >0,

q-произвольное действительное число.

Тогда при любых ограниченных начальных отклонениях от нулевого значения система будет абсолютно устойчивой.

Z=k ε

Z=F(ε)

ε

Z

0

Алгоритм анализа абсолютной устойчивости:

1. Построим годограф модифицированной

частотной характеристики

W̃(jω) = Re W(jω) + jωImW(jω).

2. Находим параметр k (наименьший из возможных), удовлетворяющий условию п.2 теоремы.

3. Анализ геометрической интерпретации условий абсолютной устойчивости:

3

jωυ(ω)

.1.

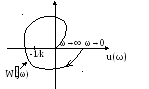
Абсолютной устойчивости нет.

3.2.

jωυ(ω)

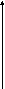
u(ω)

-1/k

ω→∞

ω→0

arctg 1/q

W̃(jω)

опорная прямая Попова, лежащая левее годографа W̃(jω).

Система абсолютно устойчива.

3.3.

jωυ(ω)

u(ω)

-1/k

W̃(jω)

ω→∞

ω→0

Заключения об абсолютной устойчивости нет.

Методы исследования нелинейных САУ

Методы разделяются на две группы:

1. Основанные на решении нелинейных дифференциальных уравнений («припасовывания», фазовых траекторий, точечных преобразований, графо-аналитические, частотный В.М. Попова, численные, моделирования);

2. Использующие линеаризацию нелинейной характеристики с последующим применением линейных методов анализа систем (малого параметра, гармонического баланса, статистической линеаризации).

\

Метод гармонической линеаризации

1. Назначение и сущность метода; гипотеза фильтра.

Метод позволяет исследовать возможность появления автоколебательных режимов, определить основные параметры автоколебаний (A, ω_а),

качественно оценить влияние нелинейностей на устойчивость и переходные процессы в системе, как устранить автоколебания или же как изменить их параметры в желаемом направлении.

Сущность метода гармонического баланса заключается в замене нелинейного элемента эквивалентным линейным, передаточный коэффициент которого не является постоянным, а зависит в общем случае от амплитуды и частоты искомых автоколебаний.

F(ε)

W_л(p)

+

-

u(t)=0

ε(t)

Z(t)

Рассматривается замкнутая система с одним НЭ. Изучается свободное движение системы, то есть движение при ненулевых начальных условиях в отсутствие внешних воздействий. В системе возможно возникновение автоколебаний. При этом Z(t)- периодическая функция, содержащая спектр гармонических составляющих.

y(t)

Если при прохождении через линейную часть системы Z(t) фильтруется так, что можно пренебречь всеми гармониками выше первой, то анализ системы можно вести методом гармонического баланса. Это предположение- необходимое условие применения метода гармонической линеаризации, его называют гипотезой фильтра, введено Е.П. Поповым. Поскольку высшие гармоники по амплитуде обычно меньше, чем первая гармоника, а линейная часть САУ узкополосная, устойчивая (могут быть нулевые корни характеристического уравнения линейной части), отсутствуют резонансные звенья, |W(jω_a)| >>|W(jkω_a)| при k >1, то во многих практических случаях гипотеза фильтра выполняется. Для приближённых расчётов последнее условие может быть смягчено и сформулировано так: наклон ЛАЧХ линейной части должен быть по крайней мере от -20 до -40 дБ/дек на частоте автоколебаний ω_а и выполнены неравенства:

при наклоне ЛАЧХ , ,

-20 дБ/дек

при наклоне ЛАЧХ , .

-40 дБ/дек