7.3. Получение следствий из данных посылок
Иногда требуется получить все следствия из данных посылок. Это можно сделать, получив формулу конъюнкции соответствующих посылок в СКНФ.
Каждый член СКНФ и всевозможные конъюнкции этих членов представляют искомое множество всех следствий.
Например, получим все следствия из посылок х и х«y:
х×(х«y)
= х(xyÚ
)
= xy = xyÚ
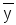y
=(xyÚ
)(xyÚy)
=
= (xÚ
)y
=(xÚ
)(yÚ
x)
= (xÚ
)(yÚ
)(yÚx).
Следовательно, формулы xÚ
,yÚ
,yÚx,
(xÚ
)(yÚ
),
(xÚ
)(yÚх),
(xÚ
)(yÚ
)(yÚx)
являются всевозможными следствиями из
данных посылок.
Дело в том, что конъюнкция истинна при истинности всех ее членов. Поэтому, невозможен случай, когда СКНФ конъюнкции посылок истинна, а какие-либо члены СКНФ или их конъюнкции ложны, что и доказывает их следование из данных посылок.
Логическое следование играет важную роль в так называемых системах с элементами искусственного интеллекта, в которых они используются в специальных подсистемах логического вывода.