
- •Оглавление
- •Случайные события. Опыт со случайными исходами. Элементарные события. Соотношения между событиями.
- •Алгебра и-алгебра событий
- •Классическое определение вероятности
- •Геометрическое определение вероятности
- •Статистическое определение вероятности
- •Аксиоматические определение вероятности. Вероятностное пространство
- •Теорема сложения вероятностей
- •Условная вероятность: определения и примеры
- •Условная вероятность как вероятностная мера случайного события в измененном вероятностном пространстве.
- •Локальная и интегральная формула Лапласа
- •Приближенные формулы Пуассона
- •Принцип практической уверенности
- •Понятие случайной величины. Дискретные случайные величины.
- •Функция распределения дискретной случайной величины
- •Числовые характеристики дискретной случайной величины
- •Биномиальный закон распределения
- •Геометрический закон распределения
- •Закон распределения Пуассона
- •Борелевские множества на прямой: определения и примеры
- •Вероятностное пространство на прямой: определения и примеры
- •Функция распределения для случайной величины общего вида и её характеристические свойства
- •Непрерывные случайные величины. Плотность вероятности и её свойства.
- •Числовые характеристики непрерывной случайной величины.
- •Равномерный закон распределения
- •Независимость двух случайных величин. Необходимое и достаточное условие независимости двух дискретных случайных величин
- •Борелевские множества на плоскости: определения и примеры
- •Вероятностное пространство для системы двух случайных величин общего вида. Независимость двух случайных величин общего вида.
- •Функция распределения двух случайных величин общего вида и её характеристические свойства
- •Система двух непрерывных случайных величин. Плотность вероятности системы двух непрерывных случайных величин и её свойства
- •Понятие функции случайной величины
- •Проверка статистических гипотез: понятие статистической гипотезы, критерий для проверки статистической гипотезы, ошибки первого и второго родов, постановка задачи…
Независимость двух случайных величин. Необходимое и достаточное условие независимости двух дискретных случайных величин
Случайные
величины X,Yназываются независимыми, если независимы
любые два события вида т.е.
т.е. - необходимость
- необходимость
Случайные величины X,Yявляются независимыми, если
 – достаточность
– достаточность
Борелевские множества на плоскости: определения и примеры
Пусть
 – действительная координатная плоскость,
а
– действительная координатная плоскость,
а – точка. Введем в рассмотрение множество
– точка. Введем в рассмотрение множество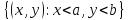 .
.
Множество
точек на координатной плоскости
называется борелевским, если оно может
быть получено из множеств вида
 применением конечного или счетного
числа операций объединения, пересечения
и теоретико-множественной разницы. В
классе борелевских множеств на плоскости
также содержится:
применением конечного или счетного
числа операций объединения, пересечения
и теоретико-множественной разницы. В
классе борелевских множеств на плоскости
также содержится:
Вся координатная плоскость

Множества вида

Отдельные точки

Множества вида

А также все множества, получаемые из перечисленных с помощью применения не более чем счетного числа указанных операций.
Вероятностное пространство для системы двух случайных величин общего вида. Независимость двух случайных величин общего вида.
Система двух случайных величин X,Yобщего вида определяется заданием вероятностного пространства, в котором:
Множество элементарных событий
 состоит из всех событий вида
состоит из всех событий вида ,
где (x,y) –
точка действительной координатной
плоскости
,
где (x,y) –
точка действительной координатной
плоскости
 -алгебра
событийSесть множество
событий вида
-алгебра
событийSесть множество
событий вида ,
где А – борелевское множество на
координатной плоскости
,
где А – борелевское множество на
координатной плоскости
На Sзадана вероятностная мераP, удовлетворяющая аксиомам теории вероятностей.
Случайные
величины X,Yназываются независимыми, если независимы
любые два события вида ,
гдеAиB–
любые два борелевских множества на
прямой, т.е.
,
гдеAиB–
любые два борелевских множества на
прямой, т.е.

Функция распределения двух случайных величин общего вида и её характеристические свойства
 – вероятность того, что система случайных
величин (X,Y)
реализуется точкой в области, множество
точек которой имеют абсциссы меньше
числа х, а ординаты меньше числаy.
ФункцияFназываетсяфункцией распределениясистемы
двух случайных величин (X,Y)
– вероятность того, что система случайных
величин (X,Y)
реализуется точкой в области, множество
точек которой имеют абсциссы меньше
числа х, а ординаты меньше числаy.
ФункцияFназываетсяфункцией распределениясистемы
двух случайных величин (X,Y)

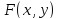 – неубывающая функция по каждому из
аргументов
– неубывающая функция по каждому из
аргументов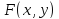 непрерывна слева по каждому из аргументов
непрерывна слева по каждому из аргументов удовлетворяет соотношениям
удовлетворяет соотношениям
Система двух непрерывных случайных величин. Плотность вероятности системы двух непрерывных случайных величин и её свойства
Система случайных величин (X,Y) называется системой непрерывных случайных величин, если её функций распределенияF(x,y) непрерывна при всех значенияхx,y.
Система
случайных величин (X,Y)
с функцией распределенияF(x,y)
имеет плотность вероятности, если
существует неотрицательная функция такая, что
такая, что

Функция
 называетсяплотностью вероятности
системы случайных величин (X,Y)
называетсяплотностью вероятности
системы случайных величин (X,Y)

Все
неравенства можно менять со строгих на
нестрогие и наоборот т.к.

Если система
непрерывных случайных величин (X,Y)
имеет плотность вероятности ,
то условие независимости этих случайных
величин можно записать в виде
,
то условие независимости этих случайных
величин можно записать в виде

Где
 – безусловные плотности вероятности
случайных величин, входящих в систему.
– безусловные плотности вероятности
случайных величин, входящих в систему.
Понятие функции случайной величины
Графиком
функции fназывается
множество
Борелевской
функцией называется такая функция f,
график которой является борелевским множеством
на плоскости.
которой является борелевским множеством
на плоскости.
Пусть
 – данная система случайных величин,
– данная система случайных величин, – данная борелевская функция. Будем
говорить, что случайная величинаYесть функцияfот случайной
величиныXи записывать
этот факт в виде
– данная борелевская функция. Будем
говорить, что случайная величинаYесть функцияfот случайной
величиныXи записывать
этот факт в виде ,
если
,
если т.е.
т.е.
Задача отыскания закона распределения заданной функции заданной случайной величины
Пусть B– борелевское множество на прямойR, тогда

Так как
 имеем
имеем

И так как

То

Таким образом

Однако

Где

Поэтому

Определив
 получим
получим
 – функция распределения случайной
величиныY
– функция распределения случайной
величиныY
Первая форма неравенства Чебышева
Пусть Х –
случайная величина, такая, что
 ,
тогда
,
тогда

Доказательство

Вторая форма неравенства Чебышева
Пусть X– случайная величина,M[X]=m– математическое ожидание, – дисперсия. Введем в рассмотрение
событие
– дисперсия. Введем в рассмотрение
событие .
Тогда
.
Тогда

Доказательство
 – противоположное событие
– противоположное событие




Теорема Чебышева
Пусть
 – независимые случайные величины такие,
что из математические ожидания одинаковы:
– независимые случайные величины такие,
что из математические ожидания одинаковы: ,
а дисперсии ограничены сверху:
,
а дисперсии ограничены сверху: .
.
Пусть
 ,
Тогда
,
Тогда
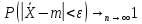
Доказательство


Теорема Бернулли
Пусть
 – число успехов в схеме Бернулли с
параметрами (n,p).
Тогда для любого
– число успехов в схеме Бернулли с
параметрами (n,p).
Тогда для любого

Доказательство
 – независимые свободные переменные,
где
– независимые свободные переменные,
где – количество успехов в испытании
Бернулли.
– количество успехов в испытании
Бернулли.





В условиях теоремы Чебышева
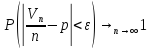
Центральная предельная теорема
Закон распределения суммы большого числа случайных величин при весьма общих условиях близок к нормальному закону распределения.
Пусть
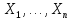 – независимые случайные величины,
имеющие конечные математические ожидания
– независимые случайные величины,
имеющие конечные математические ожидания и конечные дисперсии
и конечные дисперсии
Пусть

И выполнено
следующее условие: можно подобрать
такое
 ,
что
,
что


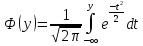
Точечные оценки неизвестных параметров закона распределения случайной величины: определение, состоятельность, несмещенность, эффективность
Статистика
 ,
дающая представление о величине
неизвестного параметра
,
дающая представление о величине
неизвестного параметра ,
называется точечной оценкой неизвестного
параметра
,
называется точечной оценкой неизвестного
параметра .
.
Оценка
 называется состоятельной, если
называется состоятельной, если она сходится по вероятности к оцениваемому
значению параметра
она сходится по вероятности к оцениваемому
значению параметра ,
т.е.
,
т.е.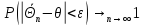
Оценка
 называется несмещенной, если её
математическое ожидание совпадает со
значением неизвестного параметра
называется несмещенной, если её
математическое ожидание совпадает со
значением неизвестного параметра ,
т.е.
,
т.е.

Оценка
 называется эффективной, если она обладает
наименьшей дисперсией.
называется эффективной, если она обладает
наименьшей дисперсией.
Состоятельные и несмещенные оценки математического ожидания и дисперсии случайной величины
 – состоятельная оценка математического
ожидания
– состоятельная оценка математического
ожидания

 – несмещенная оценка
– несмещенная оценка
 – состоятельная и несмещенная оценка
– состоятельная и несмещенная оценка
Состоятельная и несмещенная оценка для вероятности события
Оценка
 называется состоятельной, если для
называется состоятельной, если для она сходится по вероятности к оцениваемому
значению параметра
она сходится по вероятности к оцениваемому
значению параметра .
.
Оценка
 называется несмещенной, если её
математическое ожидание совпадает со
значением неизвестного параметра
называется несмещенной, если её
математическое ожидание совпадает со
значением неизвестного параметра
Доверительный интервал
Доверительным
интервалом для неизвестного параметра
 называется интервал со случайными
концами
называется интервал со случайными
концами ,
зависящими от данных наблюдений за
случайной величиной Х, для которого
известна вероятность накрытия им
значения неизвестного параметра.
,
зависящими от данных наблюдений за
случайной величиной Х, для которого
известна вероятность накрытия им
значения неизвестного параметра.
Построение приближенного доверительного интервала для неизвестной вероятности
Пусть
 ,
где
,
где – независимые случайные величины.
– независимые случайные величины.
Так как
 ,
то
,
то ,
,
Если nдостаточно велико, то в силу центральной
предельной теоремы закон распределения
случайной величины будет близок к нормальному закону
распределения с
будет близок к нормальному закону
распределения с ,
, .
.
Для
 введем в рассмотрение событие
введем в рассмотрение событие ,
где
,
где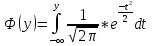 – функция распределения нормального
закона распределения
– функция распределения нормального
закона распределения
Возьмем
теперь достаточно близкое к 1 значение
 вероятности накрытия интервалом со
случайными концами
вероятности накрытия интервалом со
случайными концами Значения неизвестного параметра
неизвестного параметраpи составим уравнение
Значения неизвестного параметра
неизвестного параметраpи составим уравнение
Пусть
 – корень этого уравнения, разрешенного
относительно аргумента функции
– корень этого уравнения, разрешенного
относительно аргумента функции ,
тогда имеем
,
тогда имеем ,
откуда
,
откуда .
Следовательно, интервал со случайными
концами
.
Следовательно, интервал со случайными
концами накроет неизвестный параметрpс заданной вероятностью
накроет неизвестный параметрpс заданной вероятностью ,
т.е. будет доверительным интервалом дляp.
,
т.е. будет доверительным интервалом дляp.






