
- •Оглавление
- •Случайные события. Опыт со случайными исходами. Элементарные события. Соотношения между событиями.
- •Алгебра и-алгебра событий
- •Классическое определение вероятности
- •Геометрическое определение вероятности
- •Статистическое определение вероятности
- •Аксиоматические определение вероятности. Вероятностное пространство
- •Теорема сложения вероятностей
- •Условная вероятность: определения и примеры
- •Условная вероятность как вероятностная мера случайного события в измененном вероятностном пространстве.
- •Локальная и интегральная формула Лапласа
- •Приближенные формулы Пуассона
- •Принцип практической уверенности
- •Понятие случайной величины. Дискретные случайные величины.
- •Функция распределения дискретной случайной величины
- •Числовые характеристики дискретной случайной величины
- •Биномиальный закон распределения
- •Геометрический закон распределения
- •Закон распределения Пуассона
- •Борелевские множества на прямой: определения и примеры
- •Вероятностное пространство на прямой: определения и примеры
- •Функция распределения для случайной величины общего вида и её характеристические свойства
- •Непрерывные случайные величины. Плотность вероятности и её свойства.
- •Числовые характеристики непрерывной случайной величины.
- •Равномерный закон распределения
- •Независимость двух случайных величин. Необходимое и достаточное условие независимости двух дискретных случайных величин
- •Борелевские множества на плоскости: определения и примеры
- •Вероятностное пространство для системы двух случайных величин общего вида. Независимость двух случайных величин общего вида.
- •Функция распределения двух случайных величин общего вида и её характеристические свойства
- •Система двух непрерывных случайных величин. Плотность вероятности системы двух непрерывных случайных величин и её свойства
- •Понятие функции случайной величины
- •Проверка статистических гипотез: понятие статистической гипотезы, критерий для проверки статистической гипотезы, ошибки первого и второго родов, постановка задачи…
Закон распределения Пуассона
Дискретная случайная величина подчиняется закону распределения Пуассона, если таблица её возможных значений и соответствующих им вероятностей имеет вид
|
0 |
1 |
… |
K |
… |
|
|
|
… |
|
… |
Покажем,
что
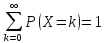

Математическое ожидание

Дисперсия

Борелевские множества на прямой: определения и примеры
Пусть R– действительная числовая ось, точка .
.
Введем
множество
 .
Множество точек на числовой оси называется
борелевским, если оно может быть получено
из множеств вида
.
Множество точек на числовой оси называется
борелевским, если оно может быть получено
из множеств вида применением конечного или счетного
числа операций объединения, пересечения
и теоретико-множественной разности.
Класс борелевских множеств весьма
широк. В этом классе содержатся:
применением конечного или счетного
числа операций объединения, пересечения
и теоретико-множественной разности.
Класс борелевских множеств весьма
широк. В этом классе содержатся:
Вся числовая ось

Множества вида

Множества вида

Отдельные точки

Множества вида

Множества вида

Множества вида

Множества вида

А также все множества, получаемые из перечисленных с помощью применения не более чем счетного числа указанных операций.
Вероятностное пространство на прямой: определения и примеры
Случайная
величина общего вида определяется
заданием вероятностного пространства

 – состоит из событий вида
– состоит из событий вида ,
где Х – точка действительной числовой
оси
,
где Х – точка действительной числовой
оси
 – множество всех подмножеств
– множество всех подмножеств вида
вида ,
гдеA– борелевское
множество наR
,
гдеA– борелевское
множество наRНа SзаданаR, удовлетворяющая всем аксиомам
Функция распределения для случайной величины общего вида и её характеристические свойства
Для
произвольного числа xвведем в рассмотрение случайное событие и вероятность этого события
и вероятность этого события .
.
 – функция распределения случайной
величины Х.
– функция распределения случайной
величины Х.
F(x) – вероятность того, что случайная величинаXпримет значение меньшее, чем х.
 – неубывающая функция
– неубывающая функция
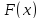 непрерывна слева, т.е.
непрерывна слева, т.е.
Для задания
случайной величины достаточно задать
её функцию распределения вместо всего
вероятностного пространства
 ,
определяющего эту случайную величину.
,
определяющего эту случайную величину.
Непрерывные случайные величины. Плотность вероятности и её свойства.
Случайная величина Х называется непрерывной, если её функция распределения F(x) непрерывна при всех значениях х.
Неотрицательная,
всюду определённая функция
 ,
удовлетворяющая условию нормировки
,
удовлетворяющая условию нормировки

И такая,
что любого х функция распределения
 непрерывной случайной величины Х есть
непрерывной случайной величины Х есть

Называется плотностью вероятностинепрерывной случайной величины Х.



 во всякой точке непрерывности х
во всякой точке непрерывности х

Числовые характеристики непрерывной случайной величины.
Пусть Х –
непрерывная случайная величина, имеющая
плотность вероятности
 .
.
 – математическое ожидание непрерывной
случайной величиныX, если
сходится интеграл
– математическое ожидание непрерывной
случайной величиныX, если
сходится интеграл
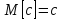 ,
c – const
,
c – const  ,
c – const
,
c – const ,
если сходится интеграл
,
если сходится интеграл ,
где
,
где – правильная функция. Функция называется
правильной, если для любого промежутка
– правильная функция. Функция называется
правильной, если для любого промежутка множество
множество есть объединение не более чем счетного
числа промежутков.
есть объединение не более чем счетного
числа промежутков.
 – дисперсия непрерывной случайной
величины Х, если сходится
– дисперсия непрерывной случайной
величины Х, если сходится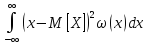

 ,
c – const
,
c – const ,
c – const
,
c – const 
 – среднеквадратическое отклонение
непрерывной случайной величины
– среднеквадратическое отклонение
непрерывной случайной величины
Равномерный закон распределения
Случайная
величина Х подчиняется равномерному
закону распределения на отрезке
 ,
если её плотность вероятности имеет
вид
,
если её плотность вероятности имеет
вид

Значение
с определяется из условия нормировки



Экспоненциальный закон распределения
Случайная величина Х подчиняется показательному (экспоненциальному) закону распределения, если её плотность вероятности имеет вид

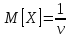

Нормальный закон распределения
Случайная величина Х подчиняется нормальному закону распределения, если её плотность вероятности имеет вид

Где aи – параметры нормального закона
распределения.
– параметры нормального закона
распределения.

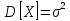
Система двух дискретных случайных величин: закон распределения
Пусть
 – система дискретных случайных величин
– система дискретных случайных величин - возможные значения Х,
- возможные значения Х,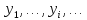 - возможные значенияY.
- возможные значенияY.
В результате
проведения опыта каждая из случайных
величин примет одно из своих значений,
т.е.

Таким образом, система 2х дискретных случайных величин может быть задана таблицей вида
|
|
|
… |
|
… |
|
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
|
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
Такую таблицу будем называть законом распределения двух случайных величин X,Y
Система двух случайных величин: безусловные и условные законы распределения случайных величин, входящих в систему. Уравнение регрессии.
Безусловный закон распределения случайной величины Х

Безусловный закон распределения случайной величины Y

Условный
закон распределения случайной величины
Y, при условии, что случайная
величина Х примет значение (i– фиксированное)
(i– фиксированное)

Условный
закон распределения случайной величины
Х, при условии, что случайная величина
Yпримет значение (j– фиксированное)
(j– фиксированное)

 – условное математическое ожиданиеYпри условии, чтоXпримет
значение
– условное математическое ожиданиеYпри условии, чтоXпримет
значение
 – условная дисперсияYпри условии, чтоXпримет
значениеx.
– условная дисперсияYпри условии, чтоXпримет
значениеx.
 – условное среднеквадратичное отклонениеYпри условии, чтоXпримет значение
– условное среднеквадратичное отклонениеYпри условии, чтоXпримет значение
 – условное математическое ожидание Х
при условии, чтоYпримет
значение
– условное математическое ожидание Х
при условии, чтоYпримет
значение
 – условная дисперсия Х при условии, чтоYпримет значение
– условная дисперсия Х при условии, чтоYпримет значение
 – условное среднеквадратичное отклонение
Х при условии, чтоYпримет
значение
– условное среднеквадратичное отклонение
Х при условии, чтоYпримет
значение
 – уравнение регрессииYнаX
– уравнение регрессииYнаX
 – уравнение регрессии Х наY
– уравнение регрессии Х наY














