5. Статистическое определение вероятности

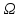– пространство элементарных событий опытаS

S–-алгебра событий

Пусть опыт Sпроводитсяnраз, пустьm– число опытов, в котором событие А произошло. Тогда относительная частота события А в серии изnповторений опытаSопределяется как

Свойства:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

6. Аксиоматические определение вероятности. Вероятностное пространство

Основные понятия, используемые при аксиоматическом подходе к построению теории вероятностей:

• Пространство элементарных событий опыта со случайными исходамиS

• Система Sподмножеств множества(связанная с даннымSсистема событийS), которая является-алгеброй

• Действительная функция , определенная наS, называемая вероятностью события, которая удовлетворяет следующим аксиомам:

1. Каждому случайному событию поставлено в соответствие неотрицательное число, называемое его вероятностью

2. 

3. Если события попарно несовместны, то

4. Если событие А равносильно наступлению хотя бы одного из попарно несовместных событий т.е., то

Тройка , гдеS– система подмножеств,S–-алгебра, а Р определена наSи удовлетворяет аксиомам 1-4, называетсявероятностным пространством.

7. Теорема сложения вероятностей

Пусть 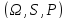– вероятностное пространство.

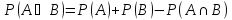
Доказательство:

По Аксиоме 3

­­­­­­­

8. Условная вероятность: определения и примеры

Мера возможности осуществления случайного события В при условии осуществлении другого события А называют условной вероятностью

Если наступление А ведет к обязательному наступлению В, то

Если наступление А ведет к обязательному ненаступлению В, то

Пример: В коробке 2 черных и 2 белых шара. Какова вероятность достать черный, при условии, что до этого достали белый?

А – достали черный шар

В – достали белый шар

– достать белый, затем черный

(A\B) – достали черный, при условии что перед этим уже достали белый

9. Условная вероятность как вероятностная мера случайного события в измененном вероятностном пространстве.

Условная вероятность – вероятность события В при осуществлении события А.

Условная вероятность события В при осуществлении события А – вероятностная мера нового вероятностного пространства 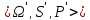, где

10. Теорема умножения вероятностей для двух событий. Независимые события. Необходимое и достаточное условие независимости.

Случайное событие В независимо от события А, если .

Теорема:

Доказательство:

Из определения условной вероятности:

Ч.т.д.

Если события А и В независимы, то

11. Теорема умножения вероятностей

Пусть – вероятностное пространство.

имеет место

Проведем доказательство индукцией по nсобытий

1. 

2. Пусть теорема верна для

3. 

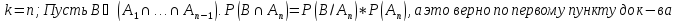
12. Неравенство Буля

Доказательство верхней оценки:

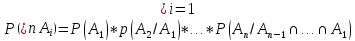
Все эти вероятности (которые в скобочках) 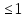, а значит

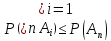
И все они меньше или равны какой-то

Доказательство нижней оценки:

Причем, (по теореме сложения)

Значит

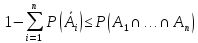
Ч.т.д.

13. Формула полной вероятности

Пусть

• – попарно несовместные события

• 

• 

Тогда

Доказательство

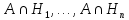– полная группа попарно несовместных событий.

14. Формула Байеса

Пусть

• – вероятностное пространство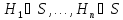

• – полная группа несовместных событий

• 

• Известны

Необходимо определить

15. Понятие независимости в совокупности семейства случайных событий.

Пусть

• – вероятностное пространство

• – семейство событий, причемIможет быть бесконечным

События данного семейства независимы в совокупности, если имеет место

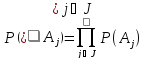
16. Способы образования новых семейств, независимых в совокупности событий из данного семейства независимых в совокупности событий

Пусть – независимы в совокупности, тогда также независимы

Пусть – независимы в совокупности, тогда также независимы

17. Схема повторных независимых испытаний

Рассмотрим опыт со случайными исходами с вероятностным пространством, где– конечное пространство элементарных событий,– множество всех подмножеств, а вероятностная мераRопределена наTзаданием вероятностей элементарных событий

Опыт со случайными исходами с вероятностным пространствомпредставляет собой одну из схем последовательным независимых испытаний и называется схемой повторных независимых испытаний.

18. Схема Бернулли

В схеме Бернулли вероятностное пространство опыта со случайными исходами(который называется испытанием Бернулли) имеет общую структуру:– пространство элементарных событий, одно из которых будем называть успехом, а другое неудачей.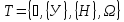, вероятностная мераRопределена на Т заданием вероятностей элементарных событий

Схема Бернулли , получающаяся приn-кратной реализации в неизменных условиях опыта(приnиспытаниях Бернулли) полностью характеризуется двумя параметрамиpиq,вероятностного пространстваопытаесть последовательность изnуспехов и неудач, возникающих при соответствующих повторенияхопыта, а вероятность любого элементарного события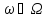, содержащегоkуспехов иn-kнеудач равна

Введем события

• – событие с 0 успехов при реализации опыта

• 

• – событие сnуспехов при реализации опыта

– полная группа несовместных событий

Пусть , тогда

Так как несовместны, то