Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный социальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

14. Методические указания 2

.pdf

Скачиваний:

Добавлен:

12.06.2015

Размер:

1.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Индивидуальное задание и его решение

9) Замечая, что (x2 - 2cosx)’ = 2x + 2sinx = 2(x + sinx), делаем соответствующую замену переменной, пользуясь формулой (3):

∫

x + sinx

dx =

x 2 - 2 cos x = t

∫

x 2 - 2cosx

2( x + sin x)dx = dt ( x + sin x)dx =

ln | t | +C =

ln | x2 − 2 cos x | +C.

10) Для вычисления этого интеграла рекомендуется изучить п.7 параграфа «Техника замены переменной в неопределённом интеграле» (см. лекцию 2):

∫

dx =

= t

= ∫

1 - t

2tdt =2∫

1 - t

dt =

t(t 2 +1)

x ( x +1)

x = t 2 dx = 2tdt

t 2 +1

		dt			tdt
= 2	∫			− ∫				= 2(I1 − I2 ).
		t 2	+1		t 2	+
							1

Интеграл I1 — это формула 9’ из таблицы интегралов. Интеграл I2 вычисляется аналогично интегралу I1 из примера 8).

Решение задачи 3

1) Этот интеграл вычисляется по схеме, реализующей соотношение

(5). Полагаем u=x и dv=e3xdx. Первое из этих равенств

продифференцируем,

а второе —

проинтегрируем: du=dx,

v = ∫e3x dx =

e3x . Получаем:

∫xe 3 x dx =

e3 x -

∫e3 x dx =

e3 x -

e3 x + C .

2) Для вычисления этого интеграла рекомендуется изучить п.1 параграфа «Техника интегрирования по частям в неопределённом интеграле» (см. лекц. 2):

u = x2 du = 2 xdx

∫ x2 cosxdx =

= x 2 × sinx - 2∫ xsinxdx =

dv = cosxdx v = sinx

u = x du = dx

= x2 × sinx + 2x × cosx - 2∫ cosxdx =

= sinxdx

v = -cosx

= x 2 × sinx + 2x × cosx - 2sinx + C .

3) Применяя теорему 6, получим:

∫ ln 5xdx =

u = ln5x du =

= x × ln 5x - ∫ x

= xln5x - x + C.

dv = dx v = x

108

Индивидуальное задание и его решение

4) Согласно формуле (5) имеем:

u = arccos2x du = −

2dx

2xdx

I = ∫arccos2xdx =

= x arccos2x + ∫

= x arccos2x

1−4x2

dv = dx v = x

1−4x2

Интеграл I1 вычисляется по формуле (3):

2xdx

1 − 4x2

= t

−

I1 = ∫

−8xdx = dt

= −

∫

= −

∫t

2 dt = −

2t 2

+C = −

1 − 4x2

+C.

1 − 4x

2xdx =

− 4

Окончательно получаем: I = x arccos 2 x −

1 − 4 x 2 + C.

5) Для вычисления этого интеграла рекомендуется изучить п.2

параграфа «Техника интегрирования по частям в неопределённом

интеграле» (см. лекц. 2):

u = arctgx du =

I = ∫ x arctg xdx =

1 + x22

arctgx −

∫

dx =

arctgx −

+ x2

xdx = dv v = ∫ xdx =

При

вычислении

интеграла

используется следующий приём

«разбавления числителя»:

1 + x 2

−1

I1 = ∫

dx =

∫

dx =

∫ dx

− ∫

= x − arctgx + C.

1 + x2

+ x2

Таким образом,

I =

arctg x −

(x − arctg x) + С.

6) Интеграл такого вида вычисляется так же, как и интегралы,

упомянутые в п.3 параграфа «Техника интегрирования по частям в

неопределённом интеграле» (см. лекцию 2):

u = cos(ln x) du = −

sin(ln x)

I = ∫cos(lnx)dx =

= x cos(ln x) + ∫sin(ln x)dx =

dx = dv v = ∫ dx =x

= = cos(ln x)

= x cos(ln x) + u sin(ln x) du x dx = x cos(ln x) + x sin(ln x) − ∫cos(ln x)dx = dx = dv v = ∫ dx = x

=x(cos(ln x) +sin(ln x)) − I.

Врезультате получили: I=x(cos(lnx)+sin(lnx))-I. Решаем это уравнение относительно I:

2I = x(cos(ln x) +sin(ln x)) I = 1 x(cos(ln x) +sin(ln x)) +С. 2

109

Индивидуальное задание и его решение

Решение задачи 4

1) Вычислим данный интеграл, заменив производную знаменателя:

7 x - 4

t = 2 x + 2 x =

t - 2

t − 2

- 4

∫

dx =

= ∫

dt =

x 2 + 2x + 5

dt = 2dx dx =

t - 2

+ 2

+ 5

∫

7t −14 −8

dt = ∫

7t − 22

dt = ∫

7t − 22

dt =

- 4t + 4

+ t - 2 + 5

t - 4t + 4 + 4t +12

t +16

= 7∫

dt −22∫

ln(t2 +16) −

arctg

+C =

+16

+16 2

ln(4x 2

+ 8x + 4 + 16) -

arctg

2 x + 2

+ C =

x +1

ln(x 2 + 2 x + 5 ) -

arctg

+ C .

2) Под знаком интеграла имеем правильную рациональную дробь (см. определение 4 из лекции 3). Разложим её на простые дроби (см. определение 5 из лекции 3), учитывая, что знаменатель дроби представляет собой произведение двух сомножителей x(x2+2x+5). Тогда, согласно формуле (9), имеем:

7 x −15	A	Bx + C	2	.
x3 + 2x 2 + 5x =	x + x2 + 2 x + 5 7 x -15 = A(x + 2x + 5) + (Bx + C )x			.
x3 + 2x 2 + 5x =	x + x2 + 2 x + 5 7 x -15 = A(x + 2x + 5) + (Bx + C )x

При x=0: -15=5А А=-3. Для определения коэффициентов В и С приравняем коэффициенты при степенях x2, x1:

	0 = A + B B = −A = 3
	= 2 A + C C = 7 − 2 A =13 .
7	= 2 A + C C = 7 − 2 A =13 .

Тогда:

∫

7 x −15

= -3∫

+ ∫

3x +13

dx.

+ 2 x

2 x +

+ 5x

Для

вычисления

интеграла

∫

3x +13

dx применяем технику,

+ 2x + 5

которую использовали в примере 1). Имеем:

∫

7 x −15

= -3∫

+ ∫

3x +13

+ 2x

2x +

+ 5x

= −3ln | x | +

ln | x 2 + 2x + 5| +5arctg

x +1

+ C.

110

Индивидуальное задание и его решение

3) Применяя формулу (9), разложим стоящую под интегралом дробь на простые дроби:

x 2 + 1	A	B	C	2	+1=A(x+3)+B(x+3)(x–
				x
( x -1) 2 × ( x + 3) =	(x -1) 2 + x -1 + x + 3			x
( x -1) 2 × ( x + 3) =	(x -1) 2 + x -1 + x + 3

1)+C(x–1) 2.

При x=1: 2=4A A=1/2; при x=-3: 10=16C C=5/8;

при x2: 1=B+C B=1– C=1–5/8=3/8.

Тогда:

I = ∫

x2 + 1

∫

dx =

( x -1)2 × ( x + 3)

( x -1)2

x -1

x + 3

Теперь исходный интеграл I вычисляется по формулам (7):

I = −	1	+	3	ln \| x −1\| +	5	ln \| x +3 \| +C.
	2(x −1)
		8			8

Решение задачи 5

1) Под знаком радикала выделим полный квадрат и вычислим данный интеграл по формуле (4) и по формуле 11 таблицы интегралов:

∫

= ∫

= ln | x +1

+ ( x +1)2

+ 2 | +C =

x 2

+ 2 x + 3

x 2 + 2x +1 + 2

( x +1) 2 + 2

= ln | x +1+ x2 + 2x +3 | +C.

2) Выделив полный квадрат под знаком радикала, сделаем в данном интеграле замену переменных (см. теорему 5):

	4x -3					4x -3						4x -3					x +	3		=t
																	x +			=t
																	2
I = ∫		dx= ∫									dx = ∫					dx =	x =t -			3	dx = dt	=

	x2 +3x -4			2		3		3 2		25			3 2		25
	x2 +3x -4			2		3		3 2		25			3 2		25
			x		+2×		× x +		-			x +		-					2
			x		+2×		× x +		-			x +		-					2
						2		2		4			2		4

= ∫

4t − 9

dt = ∫

dt − 9∫

= I1 + I2 ;

t 2 −

111

Индивидуальное задание и его решение

												2	25												1
												2	25												1
I1 = ∫		4tdt						=			t		−			=u		= 2∫				du		= 4u			+C = 4 t2 −			25	+C;
																										2
														4


	t2 −				25							2tdt = du											u					4
	t2 −											2tdt = du
						4

I2 = −9∫				dt						= −9 ln					t +		t 2 −			25				(см.			формулу 11 таблицы интегралов).
																				4
			t 2 −				25													4
			t 2 −
						4
Возвратившись к старой переменной x, окончательно получаем:

				3		2			25								3							3	2		25
I = 4 x +								−					−9 ln			x +			+		x +				−				+С =
I = 4 x +				2				−	4				−9 ln			x +	2		+		x +				−		4		+С =
				2					4								2							2			4

= 4 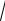x 2 +3x − 4 −9 ln | x + 3 + 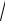x 2 +3x − 4 | +C. 2

3) Для вычисления этого интеграла рекомендуется изучить п.3 параграфа «Техника замены переменной в неопределённом интеграле» (см. лекцию 2):

∫sin3 2xdx = ∫sin2 2xsin 2xdx = ∫(1−cos2 2x)sin 2xdx =

cos2x =t

= −

∫(1−t 2 )dt =

−2sin 2xdx = dt

= −

(

dt −

∫

t 2 dt )

= −

(t −

t 3

) + С =

t 3

−

+ С =

cos 3

2 x

−

cos 2 x

+ С

∫

5x + 6 = t

sin

1 − cos

4) ∫tg 2 (5x + 6)dx =

dx =

∫tg 2tdt =

∫

dt =

∫

dt =

cos 2 t

∫

− ∫ dt

tg t

−

t + C =

tg (5 x + 6) -

(5 x

+ 6) + C .

cos 2 t

112

Индивидуальное задание и его решение

ОБРАЗЕЦ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ ПО ОПРЕДЕЛЁНЫМ, КРАТНЫМ И КРИВОЛИНЕЙНЫМ ИНТЕГРАЛАМ

Задача 1

Вычислить определённые интегралы:

1) ∫(5 + 7x − 8x3 )dx ;

2) ∫

dx ;

3) ∫2xe8 x dx .

−2

Задача 2

Вычислить площадь фигуры, ограниченной линиями:

y =

y = 9 − x 2

;

2) y =1 + x .

= 3x + 5

x = 3

Задача 3

Вычислить объёмы тел вращения:

y = sin x , 0 ≤ x ≤ π, вокруг оси Ох;

x = 3

, 0 ≤ y ≤1, вокруг оси Оу.

Задача 4

+ arcsin x),

Вычислить длину дуги плоской кривой:

y =

1 − x 2

0 ≤ x ≤1.

Задача 5

Вычислить с помощью двойного интеграла площади плоских фигур, ограниченных линиями:

y = x 2	−8x +16	;	x 2	− y 2	= 4
1)		;	2)		.
y = x +16			x = 3

Задача 6

Переходя к полярным координатам, вычислить двойной интеграл

113

Индивидуальное задание и его решение

	−	y 2			2	2	2
					x	+ y	≤ π .
			2
∫∫ 1		x		dxdy , где D :
D
						Задача 7

Вычислить координаты центра тяжести плоской фигуры,

ограниченной	линиями:	y 2 = 4x + 4 ,	y 2 = −2x + 4	(плотность
ρ = const ).
		Задача 8
Вычислить объём тела,		ограниченного	поверхностями:	y =1 + x 2 ;
z = 3x ; y = 5 ;	z = 0 и расположенного в первом октанте.
		Задача 9

Вычислить криволинейный интеграл ∫x 2 ydy − y 2 xdx , где L – дуга

				L

	cos t			π
x =	cos t		≤ t ≤	π
кривой		и 0	≤ t ≤	.
	sin t			2
y =	sin t

РЕШЕНИЕ ЗАДАЧ

Решение задачи 1

1) Для вычисления интеграла применим формулу НьютонаЛейбница (22) и свойство линейности определённого интеграла (см. также П.25):

∫

(5 + 7x − 8x3 )dx = 5 ∫dx + 7 ∫xdx −8 ∫x3dx = 5x

3−2

− 2x 4

3−2

−2

=15 − (−10)+ 63 − 28 −162 + 32 = −87,5 .

2)Здесь необходимо использовать метод замены переменной и применить формулу (23) (см. также П.26):

t = ln x

dt =

∫

dx =

= ∫t 5 dt =

x =1 t = 0

x = e t =1

=1 .

114

Индивидуальное задание и его решение

3) Для вычисления этого интеграла применим метод интегрирования по частям, то есть формулу (24) (см. также П.27):

1	u = 2x du = 2dx												1				1		1	1	e	8		1		1


∫2xe8 x dx =								1			=				xe8x			−		∫e8x dx =			−		e8 x	=
∫2xe8 x dx =	dv = e	8 x	dx v			=		1		8x	=				xe8x			−		∫e8x dx =			−		e8 x	=
0									e			4					0	4		0	4 32					0
									e			4						4			4 32
								8
								8
				e8			e8			1				7e8		+1
			=		−				+			=						≈ 652.
			=	4	−	32			+	32		=		32				≈ 652.
				4		32				32				32

Решение задачи 2

1) Вычислим площадь фигуры с помощью формулы (26) (см. также П.29), для применения которой сначала нужно построить графики заданных функций. Первая линия является параболой, а вторая – прямой. Найдём их общие точки, решив систему уравнений:

		y = 9 − x 2
			+ 5
		y = 3x	+ 5
у	y = 3x + 5	9 − x 2 = 3x + 5 x 2 + 3x − 4 = 0 x =1;−4
у	y = 3x + 5				1,2
					1,2
y = 9 − x2					.
y = 9 − x2			Таким образом в формуле (26)
		g(x)= 3x + 5 , f (x)= 9 − x 2 , a = −4 ,
-4		b =1. Имеем:
-4			1		)− (3x + 5)]dx =
О 1		х	S = ∫[(9 − x	2	)− (3x + 5)]dx =
				2

			−4
			= ∫1 (− x2 − 3x + 4)dx
			−4

3x = −1 − 3 + − 64 + + = 125

=− − + 4x = 4 24 16 .3 2 3 2 3 6

−4

2)Для нахождения площади этой фигуры будем действоватьx3 2

аналогично:

	6
y =		6	=1	+ x x 2	+ x − 6 = 0
	x

		x

	+ x
y =1

у	y =	6			x1,2 = −3;2 y1,2 = −2;3 .
	y =	x		=1 + x	Проекция фигуры D, ограниченной
		x	y		Проекция фигуры D, ограниченной
			y		заданными линиями, на ось Ох – отрезок
		D x = 4
О	2		4	х	115

Индивидуальное задание и его решение

[2;4]. То есть a = 2 , b = 4 ,

f (x)=1 + x ,

g(x)=

. Применим формулу

(26):

+ x)−

x 2

SD = ∫ (1

= x

− 6 ln x

= 4 +8 − 6 ln 4 − 2 − 2 + 6 ln 2 = 8 − 6 ln 2 ≈ 3,84 .

Решение задачи 3

Для вычисления объёма тела вращения

y =sin x

воспользуемся

формулой

(28)

(см.

также П.30):

VOx = π∫sin 2 xdx =

∫(1 − cos 2x)dx =

π2

x −

sin 2x

≈ 5.

	у
	1
		x = 3	y
z	О	х

2) Здесь вращение линии происходит вокруг оси Оу, вследствие чего применяем формулу (29) (см. также

П.31):

1	5				1

VOy = π∫3	y 2	dy =	3π		=	3π	≈1,9 .
				y 3

0	5				5
					0

Решение задачи 4

Кривая задана в декартовых координатах, поэтому будем использовать формулу (31) (см. также П.32). Сначала находим подынтегральную функцию:

y′ =	1			x			1			1
	1			x			1			1
		1 − x 2 − x				+			=		1	− x 2 .
		1 − x 2 − x				+			=		1	− x 2 .
	2 3		1 − x		2		1 − x	2		3
	2 3		1 − x				1 − x			3

Таким образом подкоренное выражение примет вид:

′	2	1				2		4 − x 2
					2
		+		1 − x			=		.
1 +[f (x)] =1			3
								3

Тогда

116

Индивидуальное задание и его решение

					x = 2sin t					π										π
					x = 2sin t
					dx = 2 costdt
	1	1			dx = 2 costdt			1		6									4	6
l =		∫ 4 - x2 dx =			x = 0 t = 0		=			∫		4 - 4sin 2 t 2 costdt =								∫cos2 tdt =

	3							3											3
	3	0			x = 1 t = p			3		0									3	0
		0								0										0

						6
				π									π
			2	6		2			1				π		π		1
			2	6		2			1				6		π		1
		=		∫(1 + cos 2t )dt =			t +				sin 2t			=		+		≈1.
									2								2
			3			3									3 3
				0									0
				0									0

Решение задачи 5

Запишем свойство

нормировки

для

двойного

интеграла:

∫∫dxdy = SD .

Применим его для вычисления площади

плоской

фигуры D с помощью двойного интеграла.

1) Чтобы

использовать свойство нормировки, нужно построить

фигуру D, описать её системой неравенств и перейти к

повторному интегралу.

Для нахождения точек пересечения

параболы и прямой решим систему

y = x +16

уравнений:

y = x 2

- 8x +16

= x +16

= x2 − 8x +16

x 2

− 8x +16 = x +16

x2 −9x = 0 x = 0;9 y

=16;25 .

1,2

Полученная фигура D является

областью 1-го типа

0 ≤ x ≤ 9

, поэтому при переходе к повторному

D :

2 −8x +16 ≤ y ≤ x +16

интегралу будем использовать формулу (46):

x+16

+16

SD = ∫∫dxdy = ∫dx

∫dy =

∫dx × y

x2 −8x+16 = ∫(x +16 - (x 2 - 8x +16))dx =

x2 −8x+16

9x 2

243

−

=121,5 .

= ∫(9x − x )dx =

2) Одна

из линий, ограничивающих фигуру D, является

гиперболой

полуосями

a = 2

b = 2

(см. лекцию 13 по

117

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.06.201567.07 Кб24131313.doc
#
29.03.201626.79 Mб53132582.rtf
#
12.08.2019585.68 Кб9133277.rtf
#
27.10.2018114.18 Кб914 Компьютерные сети.doc
#
24.12.2018430.59 Кб1114-44(сокращенный вариант).doc
#
12.06.20151.22 Mб1714. Методические указания 2.pdf
#
03.08.201984.48 Кб814. Русский романтизм. Его разновидности и хара....doc
#
11.06.201563.49 Кб271414143.doc
#
10.09.2019363.88 Кб915-20 по лекциям.docx
#
30.07.2019270.34 Кб415-28.doc
#
11.06.20153.51 Mб10915-44.doc