
Справочник по математике
.pdf
Вариант № 2
Найти пределы:
1. lim |
|
x2 2x |
. |
||
|
|
|
|
||
x 2 2x2 3x 2 |
|
||||
Ответ: |
|
2 |
. |
|
|
5 |
|
||||
|
|
|
|
||
2. lim x2 x 2 . x 1 3 
 10 x
10 x
Ответ: 18 .
3. |
lim |
x2 |
x 1 |
. |
|
|
|||
|
x 3x2 |
x 5 |
|
|
Ответ: 13 .
4. lim ctg3x sin x . x 0 cos5x
Ответ: 13 .
1
5. lim 1 2x x .
x 0
Ответ: e 2 .
6. lim ln 1 3xsin x .
x 0
Ответ: 3.
70
Вариант № 3
1. |
lim |
|
x2 x 6 |
. |
||||||||
|
|
|
|
|
|
|
|
|||||
|
x 2 3x2 7x 2 |
|
|
|||||||||
Ответ: 1. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
lim |
|
|
6 x 2 |
. |
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
x 2 |
|
x2 2x |
|
|
|||||||
Ответ: |
1 |
. |
|
|
|
|||||||
|
|
|
||||||||||
|
|
|
8 |
|
|
|
|
|
|
|||
|
|
|
|
3x x2 |
|
|
||||||
3. |
lim |
|
|
. |
|
|
|
|||||
|
|
|
|
|||||||||
|
x 4x4 1 |
|
|
|||||||||
Ответ: 0 . |
|
|
||||||||||
4. |
lim |
|
sin 2x cos5x |
. |
||||||||
|
|
|||||||||||
|
x 0 |
|
|
|
|
tg x |
|
|
||||
Ответ: 2 .
4
5. lim 1 x2 x2 .
x 0
Ответ: e4 .
6. lim e2x 1 . x 0 ln(1 4x)
Ответ: 12 .
71
5. Производная и дифференциал
Таблица 34
Производная функции
Понятие |
|
|
|
|
Определение, формула, метод |
||||||||||||
1. Производная |
|
|
lim |
y |
|
|
|
|
|
f x x f x |
. |
||||||
функции y f x |
y |
|
lim |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
x 0 x |
|
x 0 |
|
|
|
|||||||||
|
Обозначения: |
|
f |
|
x |
, |
dy |
, |
|
df |
|
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
yx , |
|
|
dx |
|
dx |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Нахождение |
Фиксировать x , дать x приращение x . Найти: |
||||||||||||||||
производной по |
1) |
f (x), |
f x x , |
y f x x f x ; |
|||||||||||||
определению |
|
|
y , y lim |
y |
|
|
|
|
|
|
|
|
|||||
|
2) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
x |
x 0 |
x |
|
|
|
|
|
|
|
|
||||
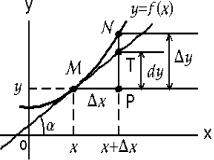
3. Геометрический |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
смысл производ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x0 tg kкас , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
где kкас – угловой коэффи- |
|||
y f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
циент наклона касательной |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. Уравнения касаУравнение касательной: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
тельной и нормали y y |
f x x x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
к графику функ- |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ции y f x в |
Уравнение нормали: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
точке M0 x0, y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y y0 |
|
|
1 |
|
x x0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
f |
x0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. Производные |
|
|
|
|
d 2 y |
|
|
|
|
|
|
|
d 3 y |
|
|
n |
|
d n y |
|
n 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||
высших порядков |
y |
|
|
|
|
2 |
, y |
|
|
|
3 y |
, y |
|
|
|
n |
|
|||||||||||
|
|
|
|
y |
|
|
|
, |
|
|
|
|||||||||||||||||
функции y f x |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
6. Физический |
Пусть s f t – уравнение движения материальной точ- |
|||||||||||||||||||||||||||
смысл производ- |
|
|
|
|
|
|
|
|
|
f t |
ds |
|
v – скорость движения точки, |
|
||||||||||||||
ной |
ки, тогда: |
|
|
|||||||||||||||||||||||||
dt |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
d 2s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f |
t dt2 |
a |
– ускорение движения точки |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||

72
Таблица 35
Формулы и правила дифференцирования
№ |
|
y |
|
|
|
|
y |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
C |
|
|
|
|
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
xn |
|
|
nxn 1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x |
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
x |
|
|
|
|
x2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
6 |
a x |
|
|
ax ln a |
|
|
|||||||||||
7 |
ex |
|
|
|
ex |
|
|
||||||||||
8 |
loga x |
|
loga e |
|
|
|
|
1 |
|
||||||||
|
x |
|
|
|
x ln a |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
ln x |
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
10 |
sin x |
|
|
cos x |
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
11 |
cos x |
|
|
sin x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
tg x |
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
cos2 x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
№ |
|
y |
|
|
|
|
|
|
|
|
|
|
y |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
ctg x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
sin2 x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
15 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
arccos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 x2 |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
16 |
arctg x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 x2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
17 |
arcctg x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x2 |
|||||||||||||||||
|
|
|
|
|
|
|
1 |
||||||||||||||
18 |
sh x |
|
|
|
|
|
|
|
ch x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
19 |
ch x |
|
|
|
|
|
|
|
sh x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
th x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ch2x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
21 |
cth x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
sh2x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
22 |
u v |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
u |
v |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23 |
u v |
|
|
v |
|
|
|
|
|
|
|||||||||||
|
u |
u v |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
u |
|
|
|
v |
|
|
|
|
|
|
|||||||||
24 |
|
|
u |
u v |
|
||||||||||||||||
|
v |
|
|
|
|
|
|
|
|
|
v2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Формула Лейбница: |
|
|
|
|
|
|
|
|
|
||||
25 |
uv |
(n) |
u |
(n) |
1 (n 1) |
|
2 (n 2) |
|
|
n 1 |
(n 1) |
uv |
(n) |
|
|
|
|
v Cnu |
v |
Cnu |
v |
Cn |
u v |
|
|
||||

73
Таблица 36
Формулы и методы дифференцирования некоторых функций
Функция |
|
Задание |
|
|
|
Формула, метод |
|
|||||||||||||||||
1. Обратная |
Пусть y f x – монотонная |
|
|
|
|
|
|
|
|
1 |
, |
|
|
|
|
|
|
|||||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
функция. Тогда существует об- |
|
|
|
|
yx |
|
xy |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ратная ей функция x y , |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
причем D E f , |
|
|
|
(x) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
( y) |
|
|
|
||||||||||||
|
E D f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. Сложная |
y f u |
y |
f g x F (x) , |
Правило цепочки: |
|
|
|
|
|
|||||||||||||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
yx |
yu ux , |
|
|
|
|||||||||||
|
u g x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u – промежуточная переменная, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x – независимая переменная |
|
|
|
F (x) f (u)g (x) |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
3. Параметри- |
|
x |
|
|
t |
|
, |
|
|
|
yx |
(t) |
|
|
y |
|
|
|
||||||
чески заданная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
функция |
|
|
|
|
|
|
(t) |
|
|
|
xt |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t – параметр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Неявная |
Функция, заданная уравнением: |
1) Продифференцировать |
||||||||||||||||||||||
функция |
|
F x, y 0 |
по x левую и правую час- |
|||||||||||||||||||||
|
|
ти уравнения, считая y |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
функцией от x . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2) Решить полученное |
|
|||||||||||||||
|
|
|
|
|
|
|
|
уравнение относительно |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Сложно- |
|
y u x v x |
Метод логарифмического |
|||||||||||||||||||||
степенная |
|
|
|
|
|
|
дифференцирования: |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
(сложно- |
|
|
|
|
|
|
|
1) ln y ln u v v ln u , |
|
|||||||||||||||
показательная) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
функция |
|
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2) |
|
y |
v ln u |
|
|
x |
, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ux |
|||||
|
|
|
|
|
|
|
|
3) yx |
u |
vx ln u v |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
u |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74
Таблица 37
Дифференциал функции
Понятие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула |
|
||||||
1. Дифференциал |
|
|
|
|
|
|
|
|
|
– первая форма записи дифференциала, |
||||||||||||||||
dy f (x) x |
||||||||||||||||||||||||||
функции y f x |
|
|
|
|
|
|
|
|
|
– вторая форма записи дифференциала |
||||||||||||||||
|
dy f (x)dx |
|||||||||||||||||||||||||
2. Правила диффе- |
1) d Cu Cdu, |
|
C const ; |
|
|
|
|
|
||||||||||||||||||
ренцирования |
2) d(u v) du dv ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3) d u v vdu udv ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
u |
|
vdu udv |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4) d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. Свойство инвари- |
Форма записи дифференциала не зависит от того, явля- |
|||||||||||||||||||||||||
антности диффе- |
ется ли переменная дифференцирования независимой |
|||||||||||||||||||||||||
ренциала первого |
переменной или сама является функцией от другой пе- |
|||||||||||||||||||||||||
порядка |
ременной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
если y f x , то |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
dy yxdx ; |
||||||||||||||||||
|
если y f u , u g x |
, то |
|
|
|
|
|
|||||||||||||||||||
|
dy yudu |
|||||||||||||||||||||||||
4. Геометрический |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PT |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x dy – прираще- |
||||
смысл дифферен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние ординаты касательной, |
||||||
циала функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проведенной в точке |
|||||||
y f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x, y |
при заданных зна- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чениях x и x |
||||||
|
|
|||||||||||||||||||||||||
5. Применение |
Нахождение приближенного значения функции |
|||||||||||||||||||||||||
дифференциала |
y f |
x в точке x x , при достаточно малых значе- |
||||||||||||||||||||||||
|
ниях x : f x x f x dy f x f x x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. Дифференциалы |
1) |
d |
2 |
y |
|
|
|
|
|
|
2 |
, |
|
|
|
|
|
|
|
|
||||||
высших порядков |
|
|
d dy y dx |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3 |
y d d |
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||
|
|
d |
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
y y dx |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
d n y d d n 1y y n dxn ; |
|
|
|
|
|
|||||||||||||||||||
|
2) |
если y f u , u g x , то |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y fuu (u)du |
|
fu (u)d u |
|||||||||||
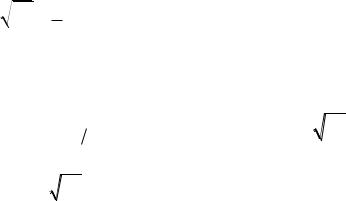
75
Варианты самостоятельной работы по теме «Производная и дифференциал»
Вариант № 1
Найти производные:
1. y 2 3 x5 3x .
x5 3x .
Решение:
Применив правило дифференцирования суммы функций (табл. 35) и формулу 2 (табл. 35), найдем производную:
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
10 |
x |
|
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
y 2x5 3 |
3x 1 |
|
x 3 |
3x 2 |
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
x2 |
|
|
|
|
103 x2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: y |
|
3 |
x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. y 3x arctg x .
Решение:
Применив правило дифференцирования произведения функций (табл. 35) и формулы 6, 16 (табл. 35), найдем производную:
|
|
|
|
3x |
|
|
|
1 |
|
y 3x |
arctg x 3x arctg x |
3x ln3 arctg x |
|
|
3x |
ln3 |
arctg x |
|
. |
|
x2 |
1 x2 |
|||||||
|
|
1 |
|
|
|
|
|||
|
y 3x |
|
arctg x |
1 |
|
|
Ответ: |
ln3 |
|
. |
|||
1 x2 |
||||||
|
|
|
|
|
3. y |
3cos x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x2 2 |
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
||
Применив правило дифференцирования частного функций (табл. 35) и |
|||||||||||||
формулы 2, 11 (табл. 35), найдем производную: |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 2 |
cos x x2 2 |
|
sin x x2 2 |
cos x 2x |
|
||||||
y 3 |
cos x |
3 |
|
||||||||||
|
x2 2 2 |
|
|
|
|
x2 2 2 |
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3sin x |
|
|
6x cos x |
|
|
|
||
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
x2 2 |
x2 2 2 |
|
|
|
|||||

76
|
|
|
|
3sin x |
|
6x cos x |
||
|
|
|
|
|
|
|
||
Ответ: |
y |
x2 2 |
x2 2 2 . |
|||||
|
||||||||
4. y arctg 2x .
Решение:
Применив правило дифференцирования сложной функции (табл. 36) и формулы 6, 16 (табл. 35), найдем производную:
|
|
|
|
y arctg 2x |
1 |
2x ln 2 |
2x ln 2 |
. |
||
|
|
|
|
1 2x 2 |
|
|||||
|
|
|
|
|
|
|
1 22x |
|||
|
|
|
|
|
2x ln 2 |
|
|
|
|
|
Ответ: |
y |
1 22x . |
|
|
|
|
||||
|
|
|
|
|
||||||
5. y ln2 x arctg 2x .
Решение:
Данная функция представляет собой произведение двух сложных функций. Применив формулы 9, 16 (табл. 35) и 2 (табл. 36), найдем производную:
|
|
|
|
|
|
|
|
|
|
2ln x arctg 2x |
|
|
2ln |
2 x |
|
||
y ln2 x arctg 2x |
ln2 x |
arctg 2x ln2 x arctg 2x |
|
|
|
|
|
|
|
. |
|||||||
x |
1 |
4x2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2ln x arctg 2x |
|
2ln2 x |
|
|
|
|
|
|
|
|
|
|||
Ответ: y |
|
x |
|
1 4x2 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
6. x3 y y2 x 1.
Решение:
Функция задана в неявном виде. Применив правило дифференцирования неявной функции (табл. 36), найдем производную:
1) 3x2 x3y 2 yy 1 0 , 2) y x3 2 y 1 3x2 y ,
3) y 1 3x2 y . x3 2 y
Ответ: y 1 3x2 y . x3 2 y

77
7. Найти уравнения касательной и нормали к графику функции
y 3x2 x в точке x0 1. Решение:
1)Найдем y0 y x0 y 1 3 1 2 1 4 .
2)Найдем производную: y 6x 1, тогда:
kкас y x0 y 1 6 1 1 7 ,
|
|
|
k |
|
|
1 |
|
|
|
|
1 |
|
1 |
. |
|||
|
|
|
норм |
y x0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
y 1 7 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
3) |
Запишем уравнение касательной (табл. 34, п. 4): |
||||||||||||||||
|
y 4 7 x 1 y 7x 3 или |
7x y 3 0 . |
|||||||||||||||
4) |
Запишем уравнение нормали (табл. 34, п. 4): |
|
|
|
|||||||||||||
|
y 4 |
1 |
x 1 y |
x |
|
|
29 |
|
или x 7 y 29 0 . |
||||||||
|
|
|
|
|
|
||||||||||||
|
7 |
|
|
|
7 |
|
|
|
7 |
|
|
|
|
|
|||
Ответ: 7x y 3 0 , x 7 y 29 0 .
Найти производные:
8. y cos x 3x .
Решение:
Данная функция является сложно-степенной. Применив правило дифференцирования сложно-степенных функций (табл. 36, п. 5), найдем производную:
1)ln y ln cos x 3x 3x ln cos x ,
2)y 3 ln cos x 3x sin x 3 cos x ln cos x xsin x , y cos x cos x
3) y y |
3 cos x ln cos x xsin x |
|
3 cos x 3x |
cos x ln cos x xsin x |
|||||
|
|
||||||||
|
|
|
|
|
cos x |
|
|
cos x |
|
3 cos x 3x 1 cos xln cos x xsin x . |
|
||||||||
|
|
|
|
|
3x 1 |
cos xln cos x xsin x . |
|||
Ответ: y |
3 cos x |
||||||||
|
x e t |
2 |
, |
|
|
|
|
||
|
|
|
|
|
|
||||
9. |
|
t |
|
|
|
|
|
|
|
|
|
sin t. |
|
|
|
|
|||
y e |
|
|
|
|
|
||||
Решение:
Функция задана в параметрическом виде. Применив правило дифференцирования параметрической функции (табл. 36, п. 3), найдем производную:

78
|
|
|
|
et |
|
|
|
|
|
|
|
|
|
|
y |
|
|
sin t |
|
|
et sin t et cost |
|
et2 t sin t cost |
|
|||
|
t |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
yx |
|
|
|
2t e t |
2 |
2t |
. |
||||||
|
xt |
|
|
t2 |
|
|
|
|
|
||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
Ответ: y |
|
et2 t cost sin t |
. |
|
|
|
|
||||||
|
|
2t |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
10. Найти y |
функции y 3cos x . |
|
|
|
|
||||||||
Решение:
Применив определение второй производной (табл. 34, п. 5) и формулы табл. 35, найдем y :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
ln 3 sin x |
ln 3 |
|
cos x |
sin x , |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
cos x |
cos x] |
|
cos x |
ln 3 ln 3 sin |
2 |
x cos x . |
||||||||||||||||||||||||||
|
ln 3 [3 |
|
|
|
ln 3 sin x sin x 3 |
|
|
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
Ответ: 3cos x ln 3 ln 3 sin2 x cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Вариант № 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Найти производные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
y x3 |
3 x |
|
|
. |
|
Ответ: y |
x4 |
|
5 5 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
y 3x arcsin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||
2. |
|
|
Ответ: y 3x ln 3 arcsin x |
|
|
|
|
. |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
8x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8x 2sin x 6 x cos x |
|
|
|
|
|
|
|||||||||||||||||||||||||
3. |
y sin x 3 . |
|
|
|
|
Ответ: y |
|
|
|
|
|
3 sin x 2 |
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
4. |
y ctg 2x2 1 . |
Ответ: y |
|
|
|
|
|
4x |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 2x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
x |
12 |
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
cos |
|
|
|
sin |
|
|
|
|
2 tg 4x |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
5. |
y |
3 |
|
|
|
|
|
. |
|
|
Ответ: y |
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||||
|
cos 4x |
|
|
|
|
|
|
|
|
|
3cos 4x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
x |
|
y y |
|
x y . |
Ответ: y |
x2 2 y 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
7. |
Найти уравнения касательной и нормали к графику функции |
y 2x3 1 в |
||||||||||||||||||||||||||||||||||||||||||||||||
точке x0 1. |
|
|
|
|
Ответ: 6x y 5 0 , |
|
|
x 6y 7 0 . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||

79
Найти производные:
8. |
y ctg x 2x . |
||||||
|
|
t |
2 |
3 |
|
||
|
x |
|
|
, |
|||
|
t2 |
|
|||||
9. |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
y |
|
|
|
|
|
. |
|
|
t |
2 |
|
|||
|
|
|
|
1 |
|||
10. Найти y |
функции |
||||||
Вариант № 3
Найти производные:
1. y 37 x5 8x2 .
x5 8x2 .
Ответ: y 2 ctg x 2x ln ctg x sin 2x 2x . sin 2x
Ответ: y t2 1 . 4t
y esin x . Ответ: y esin x cos2 x sin x .
Ответ: y |
15 |
|
16x . |
||
|
|
|
|||
|
|
|
|||
77 x2 |
|||||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
2. |
y ex log2 x . |
|
Ответ: y |
ex log2 x |
|
|
|
|
. |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ln 2 |
|
|
|
||||
|
|
|
4x |
|
|
|
|
|
|
|
4 |
cos x 2 xsin x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
y cos x 2 . |
|
Ответ: y |
|
|
|
cos x 2 2 |
|
|
|
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
4. |
y ln 1 3x2 . |
|
Ответ: y |
|
|
|
6x |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 3x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
y tg 2x ex |
2 |
|
Ответ: y |
2ex |
2 xsin x |
|
|
|
|
|
|
||||||||||||||||||
5. |
. |
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 |
2x |
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 y |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
xy y |
|
x y . |
|
|
|
x 2 y 1. |
|
|
|
|
|
|
|
|
|
||||||||||||||
6. |
|
|
Ответ: . y |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
7. |
Найти |
уравнения |
касательной |
|
|
и |
|
|
нормали |
|
к |
|
графику |
функции |
||||||||||||||||
y x2 2x 3 в точке x |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 2x y 3 0, |
x 2y 6 0 . |
|
|||||||||||||||||||
Найти производные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
x |
|
|
8. |
y tg x |
. |
|
Ответ: y |
2x tg x |
|
ln tg x |
|
|
. |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2x |
||
|
x sin t e t , |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
t2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
e |
sin t |
2t e |
|
|
|
|
||||||||||||||||
9. |
|
|
|
|
|
|
|
Ответ: y |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
t2 |
|
|
|
et cost 1 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y cost |
e . |
|
|
|
|
|
|
|
2x ln2 2 cos 2x 2x sin 2x . |
||||||||||||||||||||
10. Найти y функции y sin 2x . Ответ: |
||||||||||||||||||||||||||||||
