
Справочник по математике
.pdf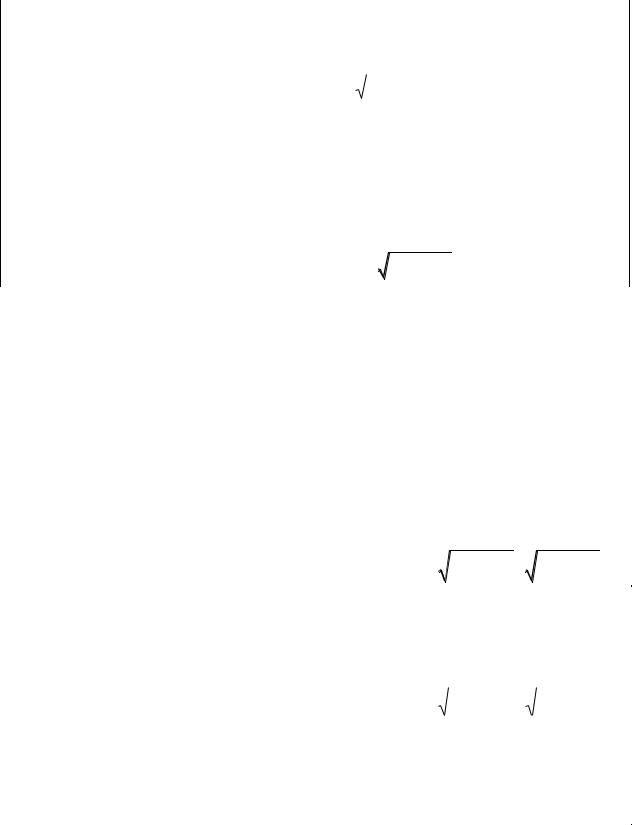
40
|
Продолжение таблицы 14 |
|
|
Понятие |
Формула, описание |
10. Приведение об- |
Для этого надо умножить все уравнение на нормирую- |
|||||||||||||||||||
щего уравнения к |
щий множитель |
|
|
|
|
|
1 |
|
|
|
, знак которого проти- |
|||||||||
нормальному виду |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
A2 B2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
воположен знаку свободного коэффициента |
|||||||||||||||||
11. Отклонение точ- |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x cos y sin p , |
||||||||||||||||||
|
|
от пря- |
если d > 0, то |
М |
и О лежат по разные стороны от |
|||||||||||||||
ки M (x , y ) |
||||||||||||||||||||
мой |
|
|
прямой; если d |
< 0, то М |
и О лежат по одну сторо- |
|||||||||||||||
|
|
|
ну от прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. Расстояние от |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
d |
|
Ax |
By |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
точки M (x , y ) до |
|
|
|
|
|
|
|
|
|
A2 B2 |
|
|||||||||
прямой |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 15 |
|||
|
|
|
|
|
|
Взаимное расположение прямых на плоскости |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Условие |
|
|
Условие |
|
|
|
Угол между прямыми |
||||||||||||||||||||||||||
параллельности |
|
перпендикулярности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1. |
|
Прямые заданы общими уравнениями: |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
A x B y C 0, A x B y C 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A1 |
|
|
|
B1 |
|
|
|
A1A2 B1B2 0 |
|
|
cos |
|
|
|
|
A1A2 B1B2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
A2 |
B2 |
A2 |
B2 |
|||||||||||||||||||||
|
|
B2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
2 |
|
|
||||||
|
|
|
|
|
|
2. Прямые заданы каноническими уравнениями: |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x x1 |
|
y y1 |
, |
|
x x2 |
|
y y2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
m1 |
|
n1 |
m2 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m n |
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
m1m2 n1n2 |
|||||||||||||||
|
1 |
|
|
1 |
|
|
|
m1m2 n1n2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
m2 |
n2 |
m2 |
n2 |
|||||||||||||||||||||
|
|
n2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
2 |
|
|
||||||
3. Прямые заданы уравнениями с угловыми коэффициентами: |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y k1x b1, |
y k2 x b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
k1 k2 |
|
|
k1 |
|
1 |
|
|
|
|
|
|
|
tg |
k2 k1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
k2 |
|
|
|
|
1 k1k2 |
|
|
|
|
|||||||||||||||||||||
41
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кривые второго порядка |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Кривая |
Каноническое |
|
|
Определение |
|
Геометрическое |
|||||||||||||||||
|
|
|
уравнение |
|
|
|
|
изображение |
|||||||||||||||
1. Эллипс |
|
|
x |
2 |
|
|
y |
2 |
|
1 |
|
|
Геометрическое место то- |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
чек плоскости, для которых |
|
|
||||||||||
|
|
|
a2 |
|
b2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
сумма расстояний до двух |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фиксированных точек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости F1 и F2 , на- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зываемых фокусами, есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
постоянная величина |
|
|
|
а и b – большая и малая полуоси, |
|
|||||||||||||||||||||
|
c2 a2 b2 |
– расстояние от центра до фокуса |
|
||||||||||||||||||||
2. Гипер- |
|
|
x |
2 |
|
|
y |
2 |
|
1 |
|
|
Геометрическое место то- |
|
|
||||||||
бола |
|
|
|
|
|
|
|
|
|
|
чек плоскости, для которых |
|
|
||||||||||
|
|
a2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
разность расстояний до |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двух фиксированных точек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости F1 и F2 , на- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зываемых фокусами, есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
постоянная величина |
|
|
|
|
x |
2 |
|
|
y |
2 |
|
1 |
|
|
Сопряженная гипербола |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
a2 |
b2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
а и b – действительная и мнимая полуоси, |
|
|||||||||||||||||||||
|
c2 a2 b2 |
– |
расстояние от центра до фокуса, |
|
|||||||||||||||||||
|
прямые |
|
y |
b |
x – асимптоты гиперболы |
|
|||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||||
3. Пара- |
|
|
|
|
y |
2 2 px |
|
|
Геометрическое место то- |
|
|
||||||||||||
бола |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чек плоскости, для которых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расстояние до некоторой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фиксированной точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости F, называемой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фокусом, равно расстоянию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
до некоторой фиксирован- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной прямой D, называе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мой директрисой |
|
|
|
р = |FQ| – |
фокальный параметр, расстояние от фокуса до ди- |
|||||||||||||||||||||
|
ректрисы |
|
|
|
|
|
|
|
|
|
|||||||||||||
42
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение таблицы 16 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Понятие |
Эллипс |
Гипербола |
|
Парабола |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Эксцен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||
|
|
|
|
b2 |
|
|
|
|
|
|
||||||||||
1 |
1 |
b2 |
||||||||||||||||||
триситет |
|
< 1, |
|
|
> 1 |
|
|
|
|
|||||||||||
a2 |
|
|
|
|
||||||||||||||||
a2 |
|
|
|
|
||||||||||||||||
|
c |
|
для окружности 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Дирек- |
Прямая, расположен- |
Прямая, расположен- |
Прямая, |
|||||||||||||||||
триса |
ная перпендикулярно |
ная перпендикулярно |
располо- |
|||||||||||||||||
|
|
|
большой оси на рас- |
действительной оси на |
женная |
|||||||||||||||
|
|
|
|
|
a |
|
|
|
a |
перпенди- |
||||||||||
|
|
|
стоянии |
|
от центра |
расстоянии |
|
от цен- |
кулярно |
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
тра |
оси сим- |
|||||||||
|
|
|
|
|
|
|
|
|
|
метрии на |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расстоянии |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
от вер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шины |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если r – |
расстояние точки до фокуса, d – расстояние точ- |
|||||
|
ки до директрисы, то |
||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
d |
||
3. Поляр- |
|
r |
p |
||||
ное урав- |
|
|
, |
||||
|
1 cos |
||||||
нение кри- |
|
|
|
|
|
|
|
вой второ- |
где р – |
расстояние от фокуса |
|||||
го порядка |
|||||||
до директрисы, – эксцентри- |
|||||||
|
ситет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 17 |
|
|
|
|
|
|
|
|
|
|
|
|
Плоскость |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тип уравнения |
|
|
|
|
|
|
|
|
|
Уравнение |
|
|
|
|
|
Геометрический смысл |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коэффициентов |
1. Общее урав- |
|
|
|
|
|
|
Ах + Ву + Сz + D = 0 |
п(А, В, С) – вектор |
||||||||||||
нение плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормали (т.е. перпен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дикуляр) к плоскости |
2. Плоскость, |
A(x x0 ) B( y y0 ) C(z z0 ) 0 |
M0(x0, y0, z0) – точка |
||||||||||||||||||
проходящая че- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на плоскости, |
рез точку, пер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п(А, В, С) – вектор |
пендикулярно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормали к плоскости |
вектору |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Уравнение |
|
x y z |
1 |
|
|
|
|
|
|
|
|
a, b и с – алгебраиче- |
||||||||
плоскости в от- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ские величины отрез- |
|
a |
|
|
|
b c |
|
|
|
|
|
|
|
|
|
|
|||||
резках |
|
|
|
|
|
|
|
|
|
|
|
|
|
ков, которые плоскость |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсекает на координат- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных осях |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. Плоскость, |
|
|
|
x x1 |
y y1 |
z z1 |
|
|
M1(x1, y1, z1) , |
|||||||||||
|
|
|
|
|||||||||||||||||
проходящая че- |
|
|
|
x |
2 |
x |
y |
2 |
y |
z |
2 |
z |
|
0 |
M 2 (x2 , y2 , z2 ) , |
|||||
рез три точки, не |
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
||||||||
|
|
|
x3 x1 |
y3 y1 |
z3 z1 |
|
|
M3(x3, y3, z3) – точки |
||||||||||||
лежащие на од- |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
на плоскости |
|||||||||||||||
ной прямой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Плоскость, |
|
|
|
x x1 |
y y1 |
z z1 |
|
|
а(т, п, l) – вектор, па- |
|||||||||||
|
|
|
|
|||||||||||||||||
проходящая че- |
|
|
|
x2 x1 |
y2 y1 |
z2 z1 |
|
0 |
раллельный плоскости, |
|||||||||||
рез две точки, |
|
|
|
|
M1(x1, y1, z1) и |
|||||||||||||||
|
|
|
|
|
|
m |
|
|
n |
|
|
l |
|
|
||||||
параллельно век- |
|
|
|
|
|
|
|
|
|
|
|
|
M 2 (x2 , y2 , z2 ) – точки |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тору |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Плоскость, |
|
|
|
|
|
x x1 |
y y1 |
z z1 |
|
|
а1(m1, n1,l1) , |
|||||||||
|
|
|
|
|
|
|||||||||||||||
проходящая че- |
|
|
|
|
|
|
m |
|
|
n |
|
l |
|
|
0 |
а2 (m2, n2,l2) – векторы, |
||||
рез точку, парал- |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
n2 |
|
l2 |
|
|
|
|
|
параллельные пло- |
||||
лельно двум не- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
скости, M1(x1, y1, z1) – |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
коллинеарным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точка на плоскости |
|
векторам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Нормальное |
|
x cos + y cos + cos – p = 0 |
cos , cos , cos – на- |
|||||||||||||||||
уравнение плос- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
правляющие косинусы |
кости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормали, р – рас- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стояние от начала ко- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ординат до плоскости |

|
44 |
|
Продолжение таблицы 17 |
|
|
Понятие |
Формула, описание |
8. Приведение об- |
Для этого надо умножить все уравнение на нормирую- |
|||||||||||||||||||||||
щего уравнения к |
щий множитель |
|
|
|
|
1 |
|
|
|
|
|
|
, знак которого |
|||||||||||
нормальному виду |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
A2 B2 C 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
противоположен знаку свободного коэффициента |
|||||||||||||||||||||
9. Отклонение точки |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos p , |
|||||||
|
|
x cos y cos z |
||||||||||||||||||||||
|
|
от плос- |
если |
d > 0, то |
М |
и О лежат по разные стороны от |
||||||||||||||||||
M (x , y , z ) |
||||||||||||||||||||||||
кости |
|
|
плоскости; если |
d |
< 0, |
|
то М |
и О лежат по одну |
||||||||||||||||
|
|
|
сторону от плоскости |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10. Расстояние от |
|
|
|
|
|
|
|
|
|
|
Cz |
|
D |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
d |
|
Ax |
|
By |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
точки M (x , y , z ) |
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C2 |
|
|||||||||||
до плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таблица 18
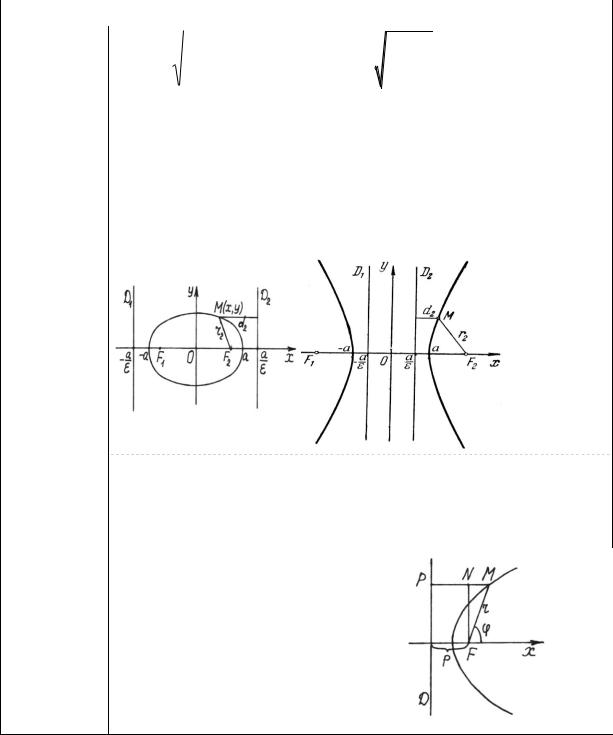
Взаимное расположение прямых и плоскостей
|
|
|
|
Условие |
|
|
|
|
|
|
Условие |
|
|
|
|
|
|
|
|
Угол между прямыми |
|
|
||||||||||||||||||||||||||||||||||
параллельности |
перпендикулярности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1. Прямые заданы каноническими уравнениями: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x x1 |
|
y y1 |
|
z z1 |
, |
|
|
x x2 |
|
y y2 |
|
z z2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
m1 |
|
n1 |
|
l2 |
|
|
|
|
m2 |
|
|
n2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
l |
|
|
m |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
l1l2 m1m2 n1n2 |
|
|
|||||||||||||||||||
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
l |
2 |
|
|
m |
|
|
n |
|
|
|
|
l1l2 m1m2 |
n1n2 |
0 |
|
|
|
|
l 2 |
m2 |
n2 |
|
|
l 2 |
m2 |
n2 |
||||||||||||||||||||||||||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
2 |
2 |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Заданы плоскость и прямая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax By Cz D 0, |
|
x x0 |
|
y y0 |
|
|
z z0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
m |
|
|
n |
|
|
|
|
|
|
|
||||||||||
Al + Bm + Cn = 0 |
|
|
A |
|
|
B |
|
C |
|
|
|
|
|
sin |
|
|
|
|
|
|
|
Al Bm Cn |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C 2 l 2 m2 n2 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l m n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Плоскости заданы общими уравнениями: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A x B y C z D 0, |
A x B y C z D 0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
|
|
1 |
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
A B C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1A2 B1B2 C1C2 |
|
|
||||||||||||||||||||||||||
|
|
|
1 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A |
|
|
B |
|
|
C |
2 |
|
|
A1A2 B1B2 |
C1C2 |
|
0 |
|
cos |
|
|
A2 |
B2 |
C 2 |
|
A2 |
B2 |
C 2 |
|||||||||||||||||||||||||||||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
2 |
2 |
2 |
|
||||||||||||||

45
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 19 |
|
|
|
|
Прямая в пространстве |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тип уравнения |
|
|
|
|
Уравнение |
|
|
Геометрический смысл |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
коэффициентов |
|||||
1. Общие уравне- |
A x B y C z D 0, |
|
Хотя бы одно из ра- |
|||||||||||||||||||
ния прямой – пря- |
1 |
1 |
1 |
|
1 |
|
|
|
венств в соотношении |
|||||||||||||
мая определена как |
A2x B2 y C2z D2 0 |
|
|
A1 B1 C1 |
не |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
линия пересечения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 |
C2 |
|
|
||||
двух плоскостей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
должно выполняться |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2. Канонические |
|
|
x x0 |
y y0 |
z z0 |
|
M0 (x0 , y0 , z0 ) – точка |
|||||||||||||||
уравнения прямой |
|
|
m |
|
|
n |
|
|
|
l |
|
|
на прямой, |
а(т, п, l) – |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направляющий (т.е. па- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
раллельный) вектор |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямой |
|
|
|
||||
|
Чтобы по заданным общим уравнениям прямой написать |
|||||||||||||||||||||
|
канонические уравнения, необходимо найти |
|
|
|
||||||||||||||||||
|
1) точку M0 (x0 , y0 , z0 ) , лежащую на этой прямой. |
Ее |
||||||||||||||||||||
|
можно найти, взяв, например, |
x0 0 и найдя |
y0 и |
z0 |
||||||||||||||||||
|
из системы: |
B1y C1z D1 0, |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
B2 y C2z D2 0; |
|
|
|
|||||||||||||
|
2) направляющий вектор а(т, п, l) этой прямой по фор- |
|||||||||||||||||||||
|
муле а = п1 п 2 , вычислив векторное произведение, по- |
|||||||||||||||||||||
|
лучим координаты направляющего вектора а(т, п, l); |
|||||||||||||||||||||
|
3) подставить найденные значения x0 , y0 , z0 , m, n и l в |
|||||||||||||||||||||
|
канонические уравнения прямой |
|
|
|
||||||||||||||||||
3. Уравнения пря- |
|
x x1 |
|
|
|
y y1 |
|
z z1 |
|
|
M1(x1, y1, z1) , |
|
||||||||||
мой, проходящей |
|
x2 x1 |
|
|
y2 y1 |
|
|
z2 z1 |
|
M 2 (x2 , y2 , z2 ) – точки |
||||||||||||
через две точки |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на прямой |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. Параметрические |
|
|
x mt x0, |
|
M0 (x0 , y0 , z0 ) – точка |
|||||||||||||||||
уравнения прямой |
|
|
|
|
nt y0, |
|
на прямой, |
а(т, п, l) – |
||||||||||||||
|
|
|
y |
|
|
направляющий вектор |
||||||||||||||||
|
|
|
z lt z |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
0 |
|
|
|
|
|
прямой |
|
|
|
|||||||||
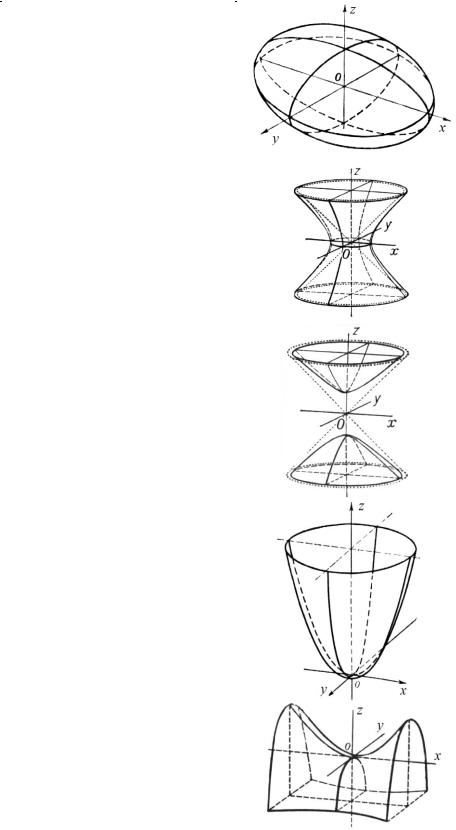
46
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 20 |
|
Поверхности второго порядка |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Название |
|
|
|
|
|
|
Уравнение |
|
Изображение |
|||||||||||||||||||
1. Эллипсоид |
|
|
x |
2 |
|
y |
2 |
|
|
z |
2 |
|
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
a2 |
b2 |
|
c2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Однополостный |
|
|
x |
2 |
|
y |
2 |
|
|
z |
2 |
1 |
|
|
||||||||||||||
гиперболоид |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
b2 |
|
|
|
|
c2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Двуполостный |
|
x |
2 |
|
|
y |
2 |
|
|
|
z |
2 |
|
1 |
|
|
||||||||||||
гиперболоид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
a2 |
b2 |
|
|
c2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Эллиптический |
|
|
|
|
|
z |
x |
2 |
|
y |
2 |
|
|
|
||||||||||||||
параболоид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
a2 |
b2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Гиперболиче- |
|
|
|
|
|
z |
x |
2 |
|
y |
2 |
|
|
|
||||||||||||||
ский параболоид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
a2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
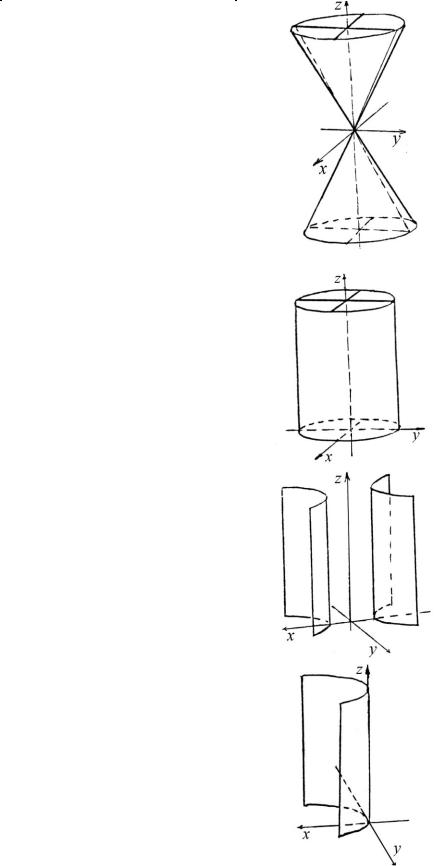
Продолжение таблицы 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Название |
|
|
|
|
Уравнение |
Изображение |
||||||||||||
6. Конус второго |
|
x |
2 |
|
|
|
y |
2 |
|
|
|
z |
2 |
0 |
|
|||
порядка |
|
|
|
|
|
|
|
|
|
|||||||||
|
a2 |
b2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
c2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. Цилиндры второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) эллиптический |
|
|
|
|
x |
2 |
|
|
y |
2 |
|
1 |
|
|||||
цилиндр |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) гиперболиче- |
|
|
|
|
x |
2 |
|
|
y |
2 |
|
1 |
|
|||||
ский цилиндр |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||
в) параболиче- |
|
|
|
|
|
y2 2 px |
|
|
||||||||||
ский цилиндр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48
Варианты самостоятельной работы по теме «Аналитическая геометрия»
Вариант № 1
|
|
|
1. Найти косинус угла между прямыми: |
|
2x 3y 5 0, |
2x y 6 0 . |
||||||||||||||||
|
|
|
Решение: Прямые заданы общими уравнениями. Воспользуемся фор- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 2 3 1 |
7 |
|
|
|
||||||
мулой из таблицы 15: cos |
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
4 9 |
4 1 |
65 |
|
||||||||||||||||||
|
|
|
Ответ: |
7 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2. Найти расстояние от точки |
M0(4;1) |
|
до прямой, проходящей через |
||||||||||||||||
точку |
M1( 1;3) параллельно вектору a(6; 1) . |
|
||||||||||||||||||||
|
|
|
Решение: Запишем сначала уравнение прямой, проходящей через точ- |
|||||||||||||||||||
ку M1 |
параллельно вектору а. Используем канонические уравнения прямой: |
|||||||||||||||||||||
|
x 1 |
|
y 3 |
. |
Приведем это |
уравнение к общему виду: (x 1) 6( y 3) , |
||||||||||||||||
|
|
|
|
|||||||||||||||||||
6 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x 6y 2 0. Воспользуемся теперь формулой расстояния от точки до пря-
мой: d |
1 4 6 1 2 |
|
|
8 |
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 36 |
37 |
|
|
|
|
|
|
||||||||||
Ответ: |
|
8 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
37 |
|
|
|
|
|
|
|
|
|
|
||||||||
3. Написать уравнение плоскости, проходящей через точку A 4,1,3 |
||||||||||||||||||
перпендикулярно вектору |
|
, если B 6, 3,8 , |
C 1,4, 2 . |
|||||||||||||||
BC |
||||||||||||||||||
|
|
|
|
|||||||||||||||
Решение: |
|
Найдем |
координаты |
BC |
(1 6,4 3, 2 8) ( 5,7, 10) . |
|||||||||||||
Воспользуемся уравнением плоскости, проходящей через точку перпендику-
лярно вектору: 5(x 4) 7( y 1) 10(z 3) 0 , 5x 7 y 10z 3 0 .
Ответ: 5x 7 y 10z 3 0 . |
|
|
|
|
|
|
|
|
|||
4. Найти расстояние от точки |
|
M0 4, 1,2 |
до плоскости, проходящей |
||||||||
через три точки M1 1,4,2 , |
M2 6,0,1 , |
M3 2, 7,2 . |
|||||||||
Решение: Запишем сначала уравнение плоскости, проходящей через |
|||||||||||
данные три точки: |
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
y 4 |
z 2 |
|
|
|
x 1 |
y 4 |
z 2 |
|
|
|
|
|
|
||||||||
|
6 1 |
0 4 |
1 2 |
|
|
|
7 |
4 |
1 |
|
0 . |
|
2 1 7 4 |
2 2 |
|
|
|
1 |
11 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

49
Раскроем определитель: 11(x 1) ( y 4) 81(z 2) 0, получим уравнение плоскости 11x y 81z 147 0 .Найдем теперь расстояние от точки до
плоскости: d |
|
11 4 1 ( 1) 81 2 147 |
|
|
60 |
|
|
|
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
121 1 6561 |
|
6683 |
|
|
|
|
|
|
|||||||||||||
Ответ: |
|
|
60 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6683 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. Найти точку пересечения прямой |
|
x 1 |
|
|
y 3 |
|
z 1 |
и плоскости |
||||||||||||||||
|
2 |
|
|
1 |
|
6 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2x y 3z 3 0 .
Решение: Перепишем уравнение прямой в параметрическом виде:
x 2t 1,y t 3,
z 6t 1.
Подставим эти равенства в уравнение плоскости:
2( 2t 1) (t 3) 3(6t 1) 3 0 ,
21t 7 0 , |
t |
1 |
. |
|
|||
|
|
3 |
|
Получили значение параметра, соответствующее точке пересечения. Осталось найти координаты точки:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
5 |
|
|
|
|||
|
|
|
|
|
x 2 |
|
|
|
|
1 |
|
|
|
, |
|
|||||||
|
|
|
|
|
|
3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
10 |
|
|
|||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
z 6 |
|
|
|
|
1 |
1. |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
Ответ: |
5 |
, |
10 |
, 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. Написать канонические уравнения прямой: x 2 y z 1 0, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x y z 2 0. |
|
Решение: Найдем точку, лежащую на прямой. Для этого возьмем, на- |
||||||||||||||||||||||
пример, x0 0 . Из системы |
|
2 y z 1 0, |
|
|
|
найдем y0 1, |
z0 1. Таким |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
y |
z 2 |
0, |
|
|
|
|
|
|
|
||||||||
образом, M0(0,1, 1) – точка, лежащая на прямой. Найдем теперь направляющий вектор прямой, как векторное произведение векторов n1(1,2,1) и n2(2, 1,1) :
