Частные случаи

1. Если ,, то система сил приводится к одной паре с моментом. В этом случае значениене зависит от выбора центраО (иначе одна и та же система сил заменяется разными, не эквивалентными парами).

2. Если ,, то система сил приводится к одной силе, т.е. к равнодействующей, приложенной в центреО.

Основная теорема статики

Для уравновешенности системы сил необходимо и достаточно чтобы ее главный вектор и главный момент относительно произвольной точки О равнялись нулю.

Условие теоремы Утверждение теоремы

Рис. 3.3

Доказательство необходимости:

Дано: .

Доказать: ,.

Если какое-то условие не выполняется, например, , то система сил приводится к равнодействующей и следовательно система не является уравновешенной. Если, система сил приводится к паре с моментоми система также не является уравновешенной, что противоречит условию.

Доказательство достаточности:

Дано: ,.

Доказать: .

Так как , то система сил приводится к паре с моментом,а так как и, то система сил находится в равновесии. Теорема доказана.

Скалярная форма условия равновесия

На основании основной теоремы статики

1)  .

Так как под корнем имеем три неотрицательных выражения, то только тогда, когда

(3.2)

2) Из второго условия теоремы следует

.

Аналогично только тогда, когда

(3.3)

Таким образом, для произвольной пространственной системы сил имеем 6 условий равновесия.

Условия равновесия для частных случаев систем сил

1. Плоская система сил

Рис. 3.4

В этом случае все силы, действующие на тело, расположены в одной плоскости. Выберем в этой плоскости оси Oxy, относительно которых рассматривается равновесие тела (рис. 3.4). Тогда условия равновесия запишутся в виде:

, ,. (3.4)

Остальные условия равновесия системы (3.2) и (3.3) обратятся в тождества 00. Поскольку все силы расположены в плоскости перпендикулярной оси z, моменты сил относительно нее определяются по формуле:

,

где h – плечо силы (рис.3.5).

Т

y

ак как в этом случае направление осиz (она всегда будет направлена на нас) не сказывается на результате, то момент силы относительно оси перпендикулярной плоскости действия сил принято называть алгебраическим моментом относитель-но точки пересечения этой оси с плоскостью или просто моментом силы относительно точки О:

(3.5)

Точка О может быть любой точкой плоскости действия сил. Условия (3.4) записанные в виде

, ,(3.6)

являются основной или первой формой условий равновесия для плоской системы сил. При решении задач статики возможно применение еще двух форм условий равновесия для плоской системы сил.

Вторая форма условий равновесия:

, ,,

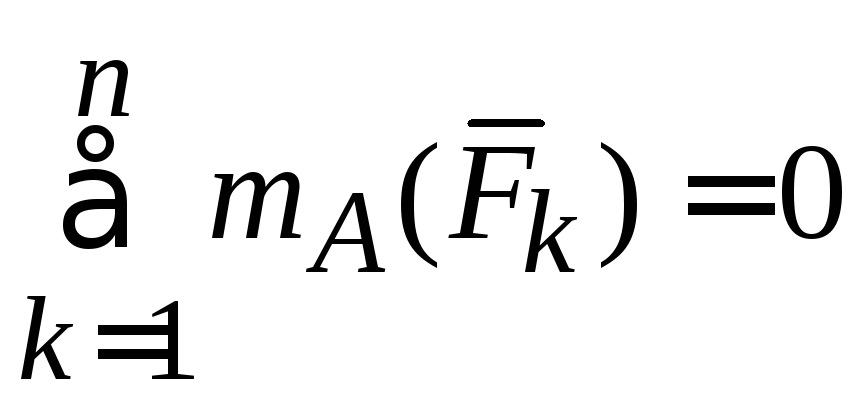где отрезок АВ, соединяющий точки А и В не должен быть перпендикулярен оси х.

Третья форма условий равновесия:

, ,,

где точки А, В, С – произвольные точки плоскости действия сил, не лежащие на одной прямой.