FTF 2 semestr.MAVRODI / 18-19

Экстремумы функции многих переменных. Необходимые и достаточные условия экстремума

Определение. Пусть функция определена на множестве 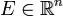и точка .

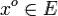Точка 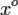называется точкой локального минимума (максимума)

функции если .

Точки локального минимума (максимума) называются точками локального экстремума.

Теорема (необходимое условие экстремума). Пусть функция определена в и имеет

Так как 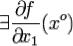, то эта производная является обычной производной функции одной переменной 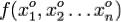в точке 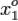. Тогда используя необходимое условие локального экстремума для

функции одной перменной получаем . Аналогично:

Если 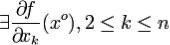получаем .

Следствие. Если функция определена в и имеет в точке 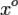локальный экстремум и дифференцируема в точке , то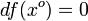

Теорема (достаточное условие локального экстремума). Пусть функция определена в 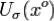и имеет в этой окрестности непрерывные частные производные второго порядка.

Пусть 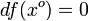. Если 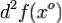является знакоопределенной квадратичной формой, тогда - точка локального экстремума, причем если - локальный минимум, а

если - локальный максимум.

,

где

.