
FTF 2 semestr.MAVRODI / 25
.pdf
Критерий интегрируемости функции.
Т е о р е м а 2. Для того, чтобы функция 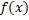 , определённая на отрезке
, определённая на отрезке  , была интегрируема на этом отрезке, необходимо и достаточно, чтобы эта функция была ограничена и удовлетворяла условию
, была интегрируема на этом отрезке, необходимо и достаточно, чтобы эта функция была ограничена и удовлетворяла условию
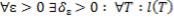 <
< . (13)
. (13)
○ Н е о б х о д и м о с т ь. Пусть функция  интегрируема на отрезке
интегрируема на отрезке 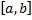 . Тогда она ограничена (теорема 1) и в силу определения интеграла
. Тогда она ограничена (теорема 1) и в силу определения интеграла
 >0:
>0: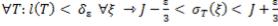 .
.
Таким образом, при каждом разбиении  отрезка
отрезка  , мелкость которого удовлетворяет условию
, мелкость которого удовлетворяет условию 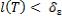 , неравенство
, неравенство
(14)
Выполняется при любой выборке 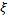 . Поэтому из левого неравенства (14) и равенства (9) следует, что
. Поэтому из левого неравенства (14) и равенства (9) следует, что
|
. |
(15) |
Аналогично из правого неравенства (14) и равенства (8) следует, что |
|
|
|
. |
(16) |
Из неравенств (15), (6) и (16) получаем цепочку неравенств |
|
|
|
, |
|
откуда следует, что |
|
|
|
. |
|
Итак, интегрируемая на отрезке функция |
удовлетворяет условию (13). |
|
Д о с т а т о ч н о с т ь. Пусть функция  ограничена на отрезке
ограничена на отрезке  и удовлетворяет условию (13). Докажем, что функция
и удовлетворяет условию (13). Докажем, что функция  интегрируема на отрезке
интегрируема на отрезке  , т.е.
, т.е.
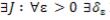 >0:
>0: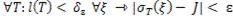 . (17)
. (17)
Воспользуемся свойством 5. Из неравенств (12) следует, что
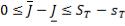 ,
,
откуда в силу (13) получаем неравенство
 ,
,
Справедливое для любого разбиения  такого, что
такого, что 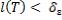 . Так как числа
. Так как числа  и
и  не зависят от
не зависят от  , то отсюда следует, что
, то отсюда следует, что
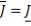 .
.
Обозначим |
|
|
|
|
|
|
|
|
|
|
(18) |
И докажем, что число |
есть интеграл от функции |
на отрезке |
. |
||
Из (12) и (18) следует, что |
|
|
|||
|
|
|
, |
|
(19) |
А из (19) и (6) в силу (13) получаем |
|
|
|||
|
|
|
|
. |
|
Это означает, что функция интегрируема на отрезке |
, а число |
есть интеграл |
|||
от |
на |
.● |
|
|
|
Классы интегрируемых функций
1.Любая функция, ограниченная и непрерывная в некотором промежутке, является интегрируемой на этом промежутке. К классу интегрируемых функций относятся также функции, ограниченные на промежутке интегрирования и имеющие на этом промежутке конечное число точек разрыва первого рода.
2.Если функция f(x) интегрируема на промежутке [a,b], то и функция c f(x), где c – константа, интегрируема на этом промежутке.
3.Если функция f(x) интегрируема на промежутке [a,b], то и функция | f(x) | интегрируема на этом промежутке.
4.Если функции f(x) и g(x) интегрируемы на промежутке [a,b], то и их сумма, разность и произведение интегрируемы на этом промежутке.
5.Если функция f(x) интегрируема на промежутке [a,b], то она интегрируема и в любой части этого промежутка.
6.Если функция f(x) интегрируема в каждой части некоторого промежутка, то она интегрируема и на всем промежутке.
7.Если значения интегрируемой функции изменить в конечном числе точек на конечные величины, то интегрируемость функции не нарушится.
Применительно к функции f(x) , которая не определена в конечном числе точек промежутка [a,b], это означает, что ни существование интеграла 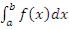 , ни его величина не зависят от значений, приписанных функции f(x) в точках ее разрыва.
, ни его величина не зависят от значений, приписанных функции f(x) в точках ее разрыва.
