FTF 2 semestr.MAVRODI / 27
.pdf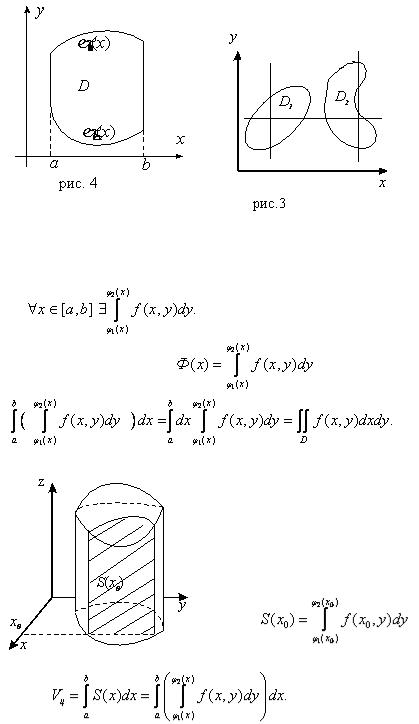
Вычисление двойного интеграла (переход к повторному).
Рассмотрим ограниченную замкнутую область D , обладающую следующим свойством: любая
прямая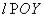 
пересекает ее границу не более, чем в двух точках. Такие области будем называть ‘правильными’ относительно оси OY (аналогично по оси OX). На рис.3: D1 − ‘правильная’ по обеим осям, D2 − ‘неправильная’ по оси OY и ‘правильная’ по оси OX. Обозначим через a и b ,
соответственно, наименьшую и наибольшую абсциссы области D . Пусть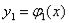
и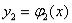 
нижняя и верхняя границы области D (рис.4).
Теорема. Пусть функция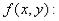 
1)интегрируема по области D;
2)
В этом случае функция |
интегрируема по х на отрезке [a,b], причем |
{
Зафиксируем произвольное значение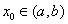 
и проведем сечение цилиндра плоскостью, параллельной оси OZ, проходящей
через прямую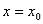 
. Пусть 
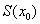− площадь сечения.
|
Тогда |
и по условию этот интеграл существует. |
|
Объем цилиндра по площадям поперечных сечений |
|
равен |
|
Так как он равен двойному интегралу от |
функции f(x,y) |
по области D, то получаем наше утверждение.} |
|
Рассмотренное представление интеграла называют переходом к повторному. В таком представлении числа а и b называют внешними пределами, а х – внешней переменной.
Соответственно, пределы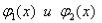 
и переменную у – внутренними.
Пример 1.
Замечания.
1. Если область D – ‘правильная’ относительно оси ОХ, то интеграл может быть представлен
следующим образом: (обозначения очевидны).
2. Если область интегрирования ‘неправильная’ относительно обеих осей, но может быть разбита на объединение ‘правильных’, то пользуясь свойством аддитивности , интеграл можно представить в виде суммы интегралов по ‘правильным’ областям.
Пример 2. Расставить пределы интегрирования: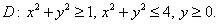 
Замечания.
1)Данная область интегрирования ‘неправильная’ по обеим осям.
2)Использовать симметрию области можно только в том случае, когда подынтегральная функции обладает такой же симметрией.
НЕОБХОДИМЫЕ ПРИЗНАКИ ПРАВИЛЬНО РАССТАВЛЕННЫХ ПРЕДЕЛОВ:
1.Внешние пределы всегда постоянны.
2.Внутренние пределы постоянны только для координатного прямоугольника.
3.Внутренние пределы могут зависеть только от внешней переменной.
4.Если верхняя или нижняя граница не записывается одной формулой, то двойной интеграл нельзя представить в виде одного повторного с внешней переменной х. Аналогичное утверждение имеет место для левой или правой границы и внешней переменной у.