
Тема 4 испр
.doc
![]() (4.38)
(4.38)
также будет удовлетворять этому уравнению.
Выполняя граничные условия (4.31), получаем
![]()
или
![]() (4.38)
(4.38)
Расположим функцию
![]() в интервале
в интервале
![]() в тригонометрический ряд Фурье:
в тригонометрический ряд Фурье:
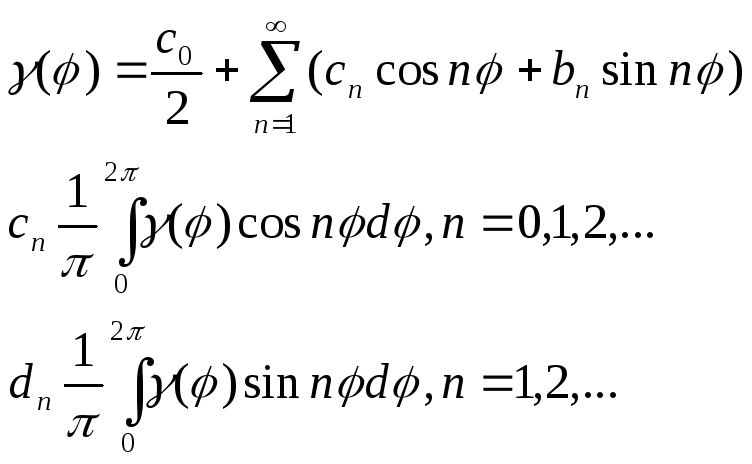 (4.39)
(4.39)
Приравняв коэффициенты в рядах Фурье (4.38) и (4.39), находим
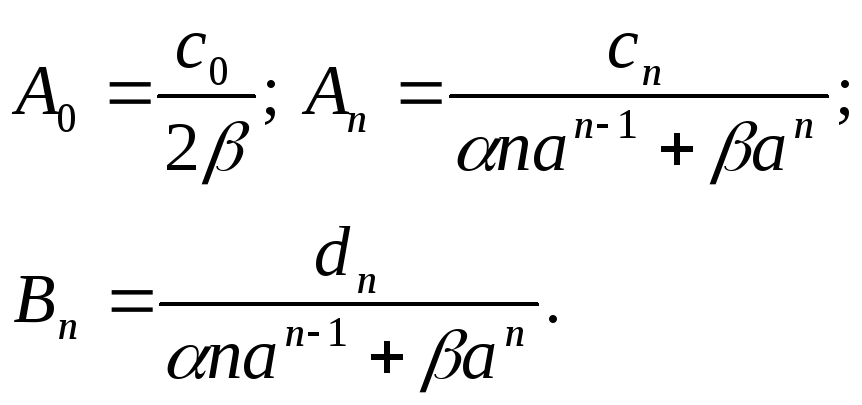 (4.40)
(4.40)
![]()
Таким образом, решение третьей краевой задачи для уравнения Лапласа в круге представимо в виде ряда (4.38) с коэффициентами, определяемыми формулами (4.39).
Задачи Дирихле и Неймана в круге. Из найденного решения третьей краевой задачи могут быть получены решения задач Дирихле и Неймана.
Если положить
![]() ,
а
,
а
![]() ,
то краевая задача (4.30) переходит в задачу
Дирихле, а её решение представимо рядом
(4.38) с коэффициентами
,
то краевая задача (4.30) переходит в задачу
Дирихле, а её решение представимо рядом
(4.38) с коэффициентами
![]() ;
;
![]() ;
;
![]() .
.
Это решение можно записать в форме
![]() .
(4.41)
.
(4.41)
Если же в задаче
(4.29) положить
![]() ,
то получим задачу Неймана для круга. В
этом случае
,
то получим задачу Неймана для круга. В
этом случае
![]() ;
;
![]()
а формула (4.40) для
коэффициента
![]() устанавливает условие (???) разрешимости
задачи Неймана
устанавливает условие (???) разрешимости
задачи Неймана
![]() .
.
Поэтому решение задачи Неймана имеет вид
![]() .
(4.42)
.
(4.42)
Замечание. Если в формулах (4.41) и
(4.42) значение
![]() считать равным
считать равным
![]() ,
то они будут определять решение внешних
для круга задач Дирихле и Неймана.
,
то они будут определять решение внешних
для круга задач Дирихле и Неймана.
Интеграл Пуассона.
Получим иную
форму записи решения задачи Дирихле
для круга. Для этого преобразуем решение
(4.46), подставляя в него значения
коэффициентов
![]() и
и
![]() ,
,
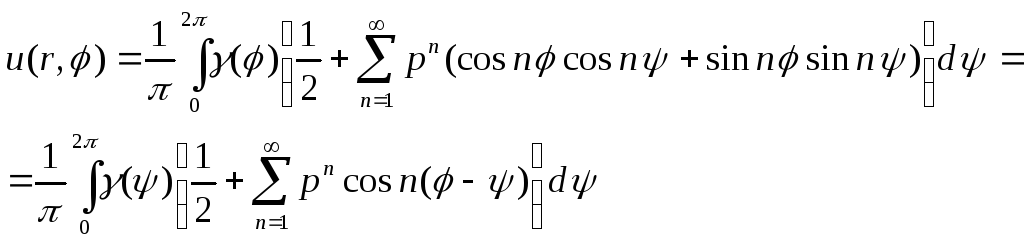 (4.43)
(4.43)
Замечая, что
![]() ,
,
находим
![]()
![]() .
.
Так как
![]() ,
то, вычислив суммы геометрических
прогрессий, получим
,
то, вычислив суммы геометрических
прогрессий, получим
![]()
![]()
Подставляя найденное
значение
![]() в уравнение (4.43), получаем решение задачи
Дирихле для круга в форме
в уравнение (4.43), получаем решение задачи
Дирихле для круга в форме
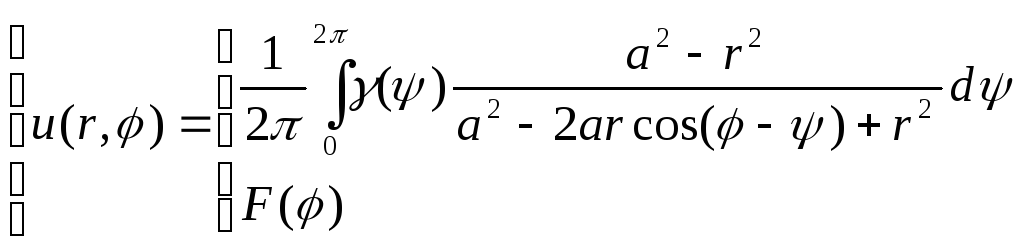
![]() (4.44)
(4.44)
Интеграл в правой части формулы (4.44) называют интегралом Пуассона для круга.
Внешняя краевая задача.
Для решения внешней
краевой задачи (4.29) необходимо положить
коэффициент
![]() и выбрать решение в виде
и выбрать решение в виде
![]() ,
т. к. решение внешней задачи должно быть
ограниченно на
,
т. к. решение внешней задачи должно быть
ограниченно на
![]() .
.
Тогда частные решения задачи примут вид:
![]() ,
(4.45)
,
(4.45)
а общее решение запишется в виде:
![]() .
(4.46)
.
(4.46)
Аналогично задачи Дирихле внутри круга, для внешней задачи, используя граничные условия, получаем коэффициенты:
![]() ;
;
![]() ;
;
![]() (4.47)
(4.47)
а решение внешней задачи Дирихле примет вид:
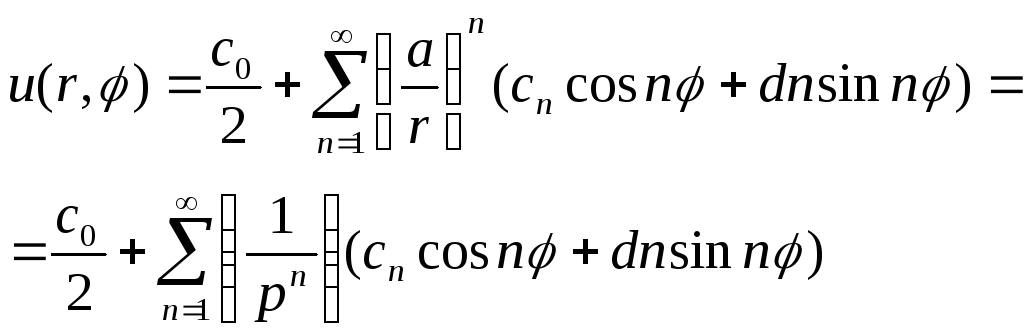 (4.48)
(4.48)
Решение внешней краевой задачи можно представить как интеграл Пуассона:
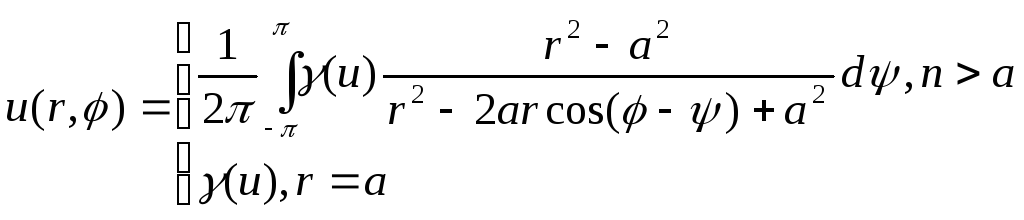 (4.49)
(4.49)
Задача Дирихле
в кольце.
Приведем теперь решение задачи Дирихле
в кольце, внутренняя граница которого
есть окружность радиуса
![]() ,
а внешняя – окружность радиуса
,
а внешняя – окружность радиуса
![]() .
Эту задачу можно записать следующим
образом:
.
Эту задачу можно записать следующим
образом:
![]() ;
(4.50)
;
(4.50)
![]() .
(4.51)
.
(4.51)
Представляя решение
уравнения (4.50) в форме (4.32), придем к
задаче на собственные значения (4.34) для
функции
![]() и к решению в интервале
и к решению в интервале
![]() уравнения (4.36).
уравнения (4.36).
Общее решение уравнения (4.36) имеет вид
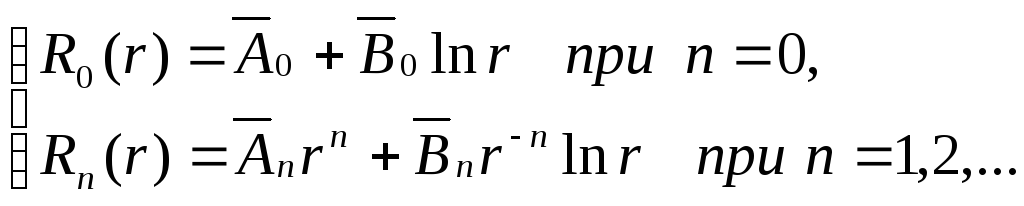 (4.52)
(4.52)
Здесь в отличие
от задачи для круга нужно сохранить оба
слагаемых, так как точка
![]() находится вне кольца.
находится вне кольца.
Поэтому с учетом формул (4.35) и (4.52) частные решения уравнения (4.50) можно записать в виде
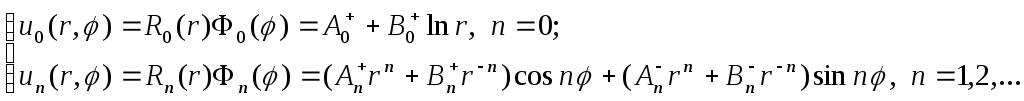
Здесь
![]() ;
;
![]() ;
;
![]() ;
;
![]() - произвольные постоянные.
- произвольные постоянные.
Функция
![]() ,
определяется как суперпозиция этих
частных решений:
,
определяется как суперпозиция этих
частных решений:
![]() ,
(4.53)
,
(4.53)
будет удовлетворять линейному однородному уравнению (4.50).
Подставив (4.53) в граничные условия (4.51), получим
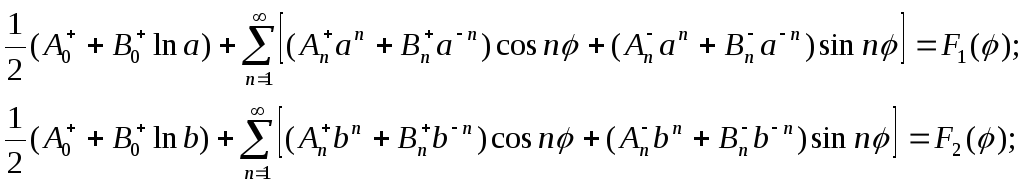 (4.54)
(4.54)
Эти соотношения
представляют собой разложение заданных
функций
![]() и
и
![]() в тригонометрические ряды Фурье. Вычислим
коэффициенты Фурье этих функций:
в тригонометрические ряды Фурье. Вычислим
коэффициенты Фурье этих функций:
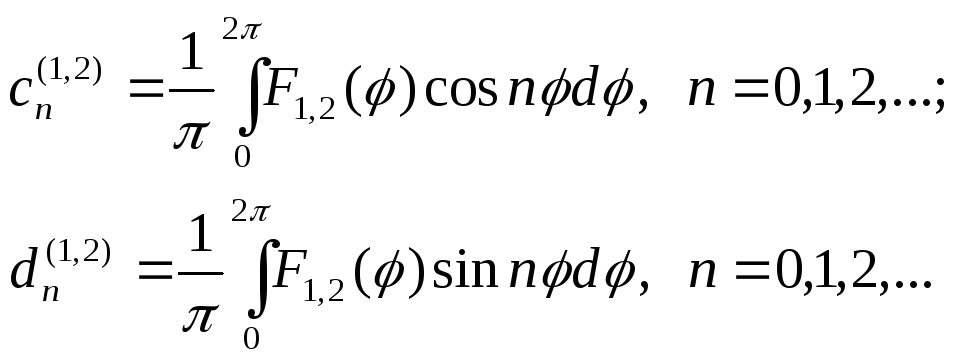
Тогда из уравнений (4.54) находим
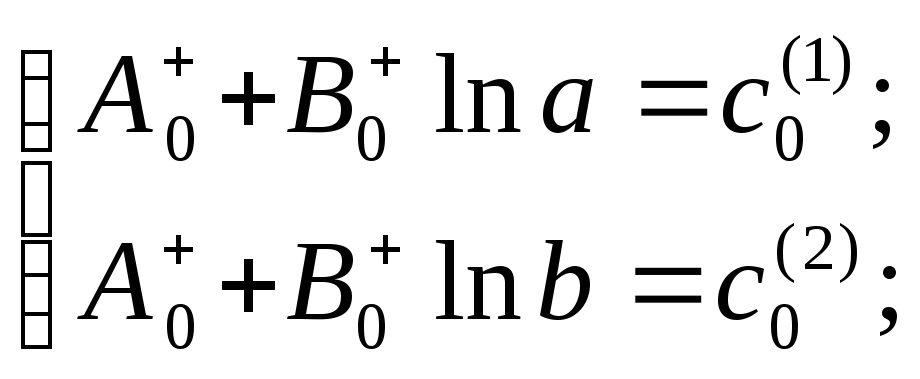
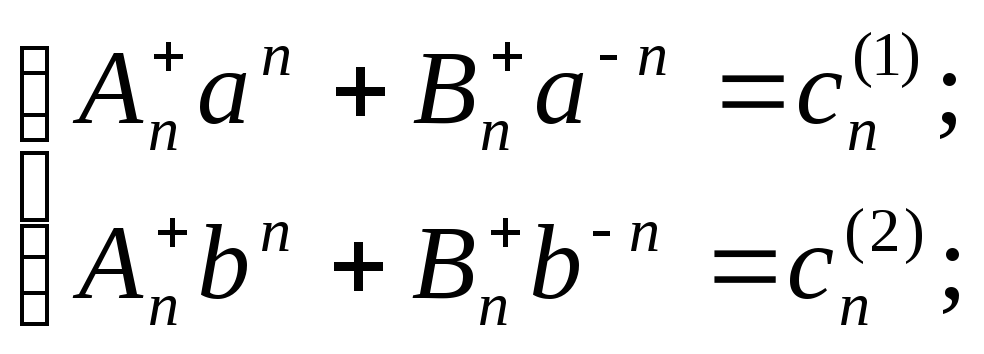
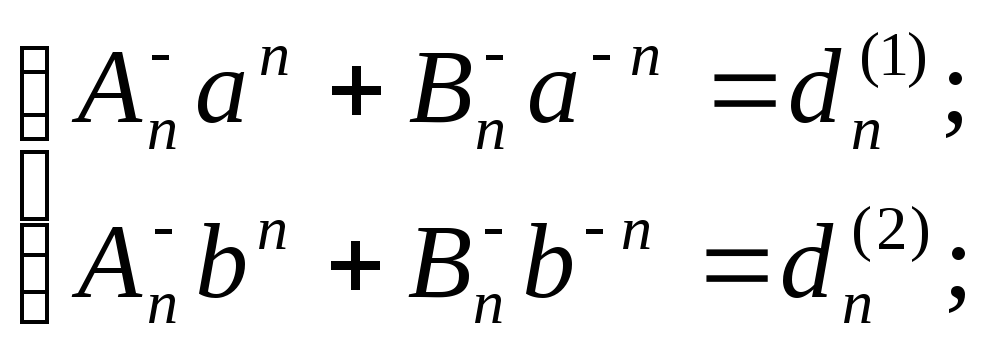
Так как
![]() и
и
![]() ,
то эти системы однозначно разрешимы:
,
то эти системы однозначно разрешимы:
 ;
;
 ;
;
![]() ;
;
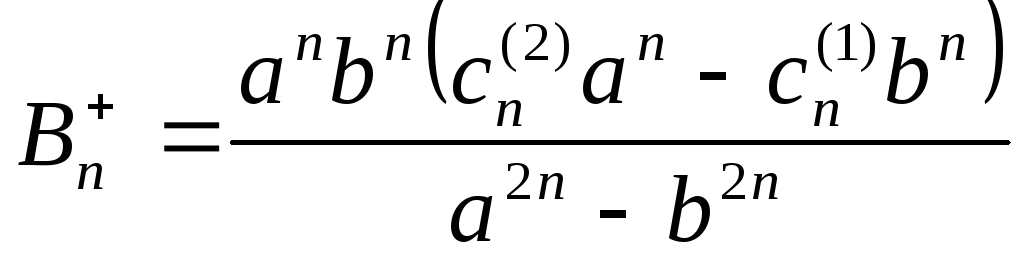 ;
;
![]() ;
;
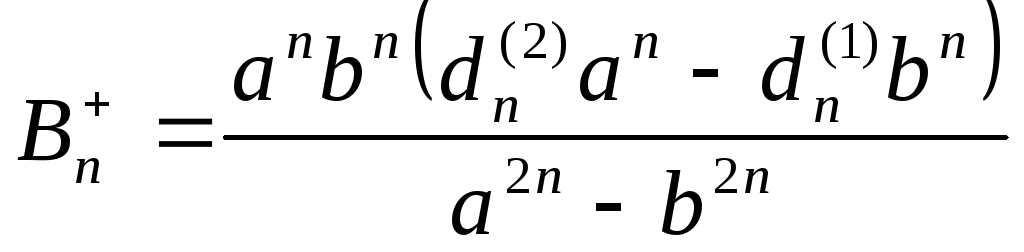 .
.
Подставляя значения этих коэффициентов в уравнение (4.53), получаем решение задачи Дирихле в кольце.
4. Рассмотрим физическую природу и свойства объемного, логарифмического и поверхностного потенциалов. Для этого воспользуемся электростатической аналогией.
Пусть в некоторой
точке
![]() помещен заряд
помещен заряд
![]() .
Потенциал поля, создаваемого этим
зарядом в точке
.
Потенциал поля, создаваемого этим
зарядом в точке
![]() равен:
равен:
![]()
Далее предположим,
что заряд
![]() распределен в области
распределен в области
![]() непрерывным образом с плотностью
непрерывным образом с плотностью
![]() .
Определим потенциал поля, создаваемого
этим зарядом в точке
.
Определим потенциал поля, создаваемого
этим зарядом в точке
![]() .
Для этого разобьем объем
.
Для этого разобьем объем
![]() на элементарные области
на элементарные области
![]() .
Также предложим, что заряд, рассредоточенный
в элементарном объеме
.
Также предложим, что заряд, рассредоточенный
в элементарном объеме
![]() ,
можно считать точечным. Тогда имеем:
,
можно считать точечным. Тогда имеем:
![]()
Выполняя интегрирование в последнем выражении, имеем:
![]() (4.55)
которое
совпадает с первым слагаемым в (4.15).
(4.55)
которое
совпадает с первым слагаемым в (4.15).
Интеграл (5.???????)
однозначно определен, если точка
![]() не принадлежит области
не принадлежит области
![]() .
В противном случае этот интеграл является
несобственным, так как подынтегральная
функция при
.
В противном случае этот интеграл является
несобственным, так как подынтегральная
функция при
![]() обращается в бесконечность, т.е. имеет
особенность.
обращается в бесконечность, т.е. имеет
особенность.
Укажем простейшие свойства объемного потенциала:
-
Если функция
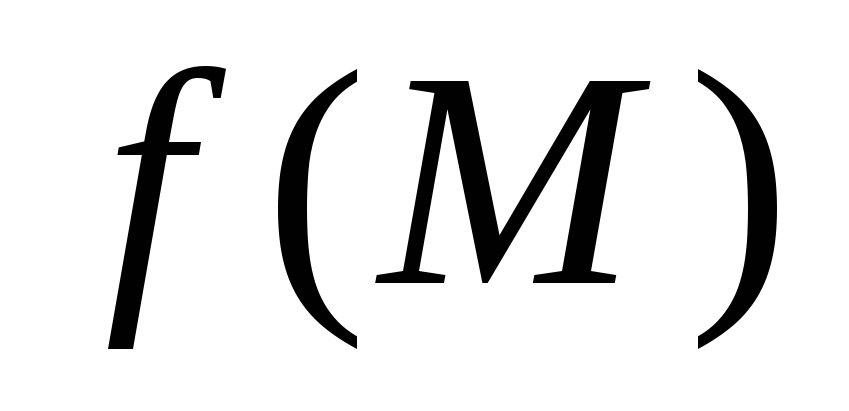 непрерывна и ограничена в объеме
непрерывна и ограничена в объеме
 ,
то объемный потенциал
,
то объемный потенциал
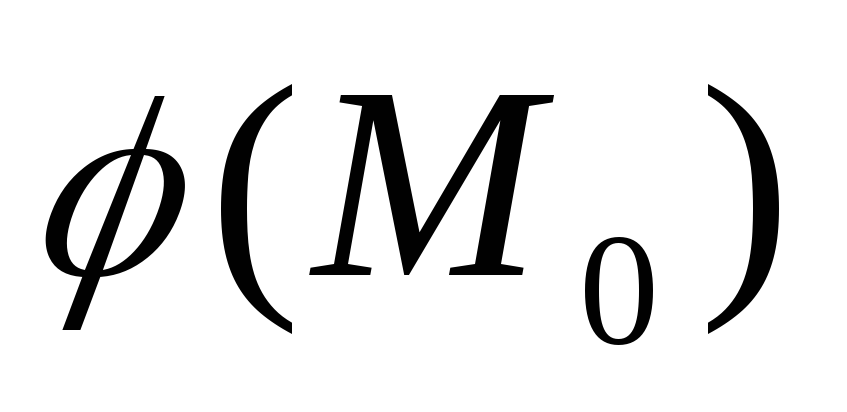 непрерывен во всем пространстве;
непрерывен во всем пространстве; -
Если функция
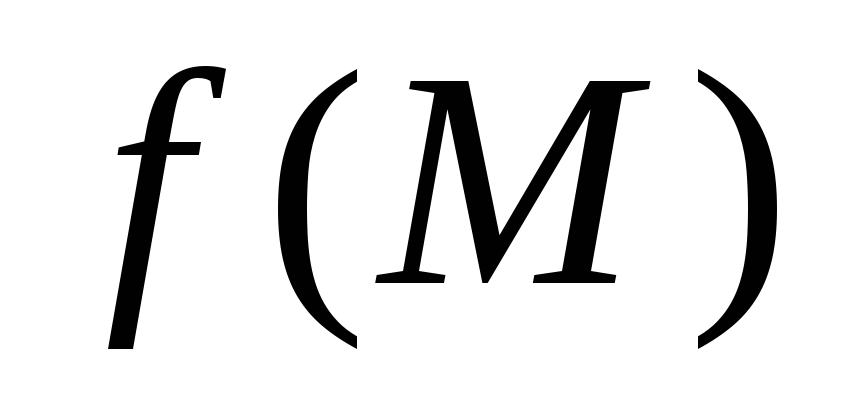 непрерывна и ограничена в объеме
непрерывна и ограничена в объеме
 ,
то объемный потенциал
,
то объемный потенциал
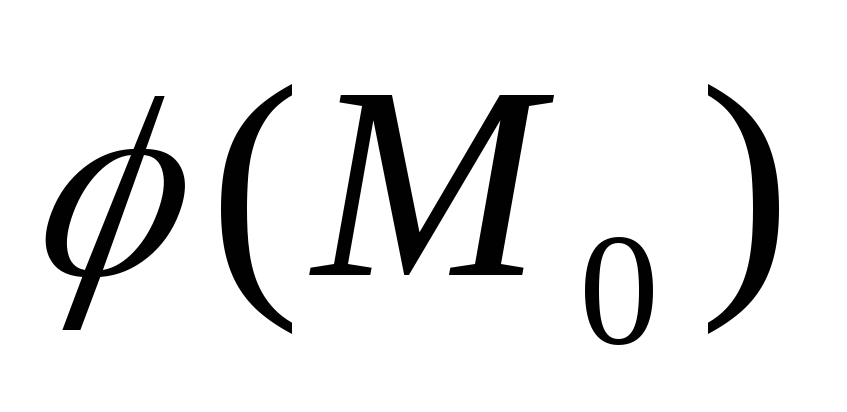 имеет непрерывные частные производные
первого порядка во всем пространстве.
имеет непрерывные частные производные
первого порядка во всем пространстве. -
Если функция
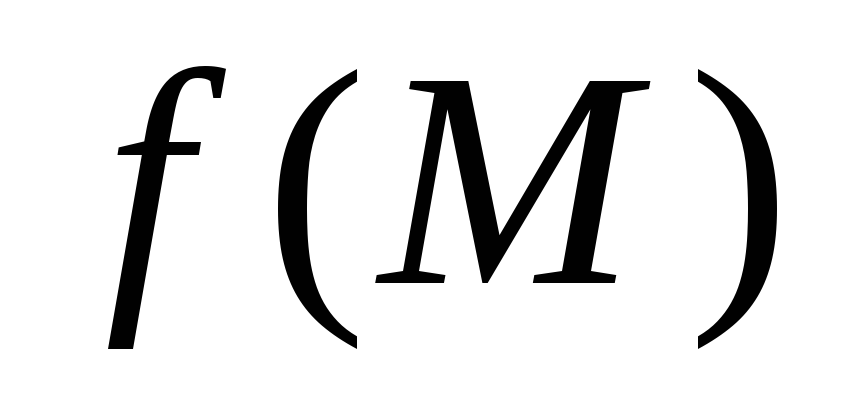 непрерывна и ограничена в области
непрерывна и ограничена в области
 ,
то вне области
,
то вне области
 объемный потенциал (5.????????) удовлетворяет
уравнению Лапласа:
объемный потенциал (5.????????) удовлетворяет
уравнению Лапласа:
![]()
а внутри области
![]() - уравнению Пуассона
- уравнению Пуассона
![]()
Индекс
![]() у оператора Лапласа обозначает в нашем
случае дифференцирование по переменным
у оператора Лапласа обозначает в нашем
случае дифференцирование по переменным
![]() .
.
Пусть далее заряд
в пространстве распределен
«плоскопараллельным» образом, т. е.
закон его распределения зависит только
от
![]() и
и
![]() .
Потенциал создаваемого этим полем
заряда, очевидно, не зависит от координаты
.
Потенциал создаваемого этим полем
заряда, очевидно, не зависит от координаты
![]() и задачу можно считать плоской.
и задачу можно считать плоской.
Пусть помещенный
на плоскости заряд является точечным.
В пространстве задача определения поля,
создаваемого этим зарядом, эквивалентна
поиску потенциала бесконечно длинной
равномерно заряженной с линейной
плотностью
![]() нити. Потенциал исследуемого поля равен:
нити. Потенциал исследуемого поля равен:
![]()
Рассмотрим более
общий случай, когда заряд
![]() непрерывно распределен в некоторой
области
непрерывно распределен в некоторой
области
![]() с плотностью
с плотностью
![]() .
Как и при введении объемного потенциала,
разобьем поверхность
.
Как и при введении объемного потенциала,
разобьем поверхность
![]() на элементарные площадки
на элементарные площадки
![]() .
Будем предполагать, что внутри каждой
их площадок
.
Будем предполагать, что внутри каждой
их площадок
![]() заряд можно считать точечным. Тогда
потенциал, создаваемый зарядами,
находящимися внутри элементарной
площадки, равен:
заряд можно считать точечным. Тогда
потенциал, создаваемый зарядами,
находящимися внутри элементарной
площадки, равен:
![]()
Выполняя интегрирование в последнем выражении, получаем:
![]() (4.56)
Нетрудно
заметить, что выражение логарифмического
потенциала (4.56) в точности совпадает с
(4.18).
(4.56)
Нетрудно
заметить, что выражение логарифмического
потенциала (4.56) в точности совпадает с
(4.18).
Как и объемный
потенциал, логарифмический потенциал
определен однозначно, если точка
![]() лежит вне поверхности
лежит вне поверхности
![]() .
Однако, имеется одно существенное
отличие. Если точка
.
Однако, имеется одно существенное
отличие. Если точка
![]() удалена от
удалена от
![]() на бесконечно большом расстоянии, то
логарифмический потенциал имеет
особенность, связанную с неопределенностью
в вычислении логарифма.
на бесконечно большом расстоянии, то
логарифмический потенциал имеет
особенность, связанную с неопределенностью
в вычислении логарифма.
Если точка
![]() лежит внутри
лежит внутри
![]() ,
то интеграл (4.56) является несобственным,
а подынтегральная функция имеет
особенность при
,
то интеграл (4.56) является несобственным,
а подынтегральная функция имеет
особенность при
![]() .
.
Можно показать,
что для логарифмического потенциала
также справедливы свойства, указанные
для объемного потенциала. В частности,
если функция
![]() непрерывна и ограничена в области
непрерывна и ограничена в области
![]() ,
то логарифмический потенциал (4.56)
удовлетворяет внутри
,
то логарифмический потенциал (4.56)
удовлетворяет внутри
![]() уравнению Пуассона:
уравнению Пуассона:
![]()
в вне
![]() - уравнению Лапласа:
- уравнению Лапласа:
![]()
Здесь
![]()
Если электрический
заряд с объемной плотностью
![]() расположен в небольшом слое толщиной
расположен в небольшом слое толщиной
![]() около поверхности
около поверхности
![]() ,
а поле исследуется на расстоянии
,
а поле исследуется на расстоянии
![]() много большем
много большем
![]() учет толщины поверхности не имеет
смысла. По этой причине вместо объемного
потенциала целесообразно рассматривать
поверхностный потенциал.
учет толщины поверхности не имеет
смысла. По этой причине вместо объемного
потенциала целесообразно рассматривать
поверхностный потенциал.
Рассмотрим поле,
создаваемое зарядами, распределенными
по поверхности. Потенциал этого поля
выражается через поверхностную плотность
заряда
![]() и равен:
и равен:
![]() (4.57)
Потенциал
(5.48) носит название потенциала
простого слоя.
(4.57)
Потенциал
(5.48) носит название потенциала
простого слоя.
Д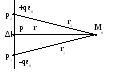 ругим
типом поверхностного потенциала является
потенциал двойного слоя. Рассмотрим
диполь, образованный двумя зарядами
ругим
типом поверхностного потенциала является
потенциал двойного слоя. Рассмотрим
диполь, образованный двумя зарядами
![]() и
и
![]() ,
расположенными в точках
,
расположенными в точках
![]() и
и
![]() в окрестности поверхности
в окрестности поверхности
![]() .
Введем дипольный момент
.
Введем дипольный момент
![]()
этой системы
зарядов. Здесь
![]() - расстояние между точками
- расстояние между точками
![]() и
и
![]() .
.
Потенциал диполя
![]() в некоторой точке
в некоторой точке
![]() может быть найден на основе принципа
суперпозиции:
может быть найден на основе принципа
суперпозиции:
![]() (4.58)
Здесь
(4.58)
Здесь
![]() Пусть точка
Пусть точка
![]() удовлетворяет условиям:
удовлетворяет условиям:
![]() Выбирая на отрезке
Выбирая на отрезке
![]() некоторую среднюю точку, перепишем
(4.58) в виде
некоторую среднюю точку, перепишем
(4.58) в виде
![]() (4.59)
Вычисляя в
(4.59) производную по направлению
(4.59)
Вычисляя в
(4.59) производную по направлению
![]() ,
получаем:
,
получаем:
![]()
Теперь рассмотрим
две поверхности
![]() и
и
![]() ,
находящиеся друг от друга на малом
расстоянии
,
находящиеся друг от друга на малом
расстоянии
![]() .
Пусть на этих поверхностях распределены
заряды
.
Пусть на этих поверхностях распределены
заряды
![]() и
и
![]() с поверхностной плотностью
с поверхностной плотностью
![]() В этом случае дипольный момент
В этом случае дипольный момент
![]() также оказывается распределенным с
некоторой поверхностной плотностью
также оказывается распределенным с
некоторой поверхностной плотностью
![]() .
.
В частности, дипольный момент элемента
поверхности
частности, дипольный момент элемента
поверхности
![]() оказывается равным
оказывается равным
![]() .
.
Тогда, в соответствии
с (4.59), потенциал зарядов элемента
поверхности в точке
![]() оказывается равным
оказывается равным
![]() (4.60)
Здесь
(4.60)
Здесь
![]() - нормаль к элементу
- нормаль к элементу
![]() ,
проведенная в точке
,
проведенная в точке
![]() .
Направление нормали
.
Направление нормали
![]() эквивалентно направлению
эквивалентно направлению
![]() для системы двух зарядов.
для системы двух зарядов.
Используя принцип суперпозиции, проинтегрируем (4.60). В результате получим:
![]() (4.61)
Знак “ – ”
соответствует случаю, когда внутренняя
сторона поверхности
(4.61)
Знак “ – ”
соответствует случаю, когда внутренняя
сторона поверхности
![]() заряжена отрицательно, а внешняя –
положительно.
заряжена отрицательно, а внешняя –
положительно.
Величина (4.61) совпадает с (5.????????) и называется потенциалом двойного слоя.
Потенциал двойного
слоя в некоторой точке
![]() терпит разрыв и удовлетворяет соотношениям:
терпит разрыв и удовлетворяет соотношениям:
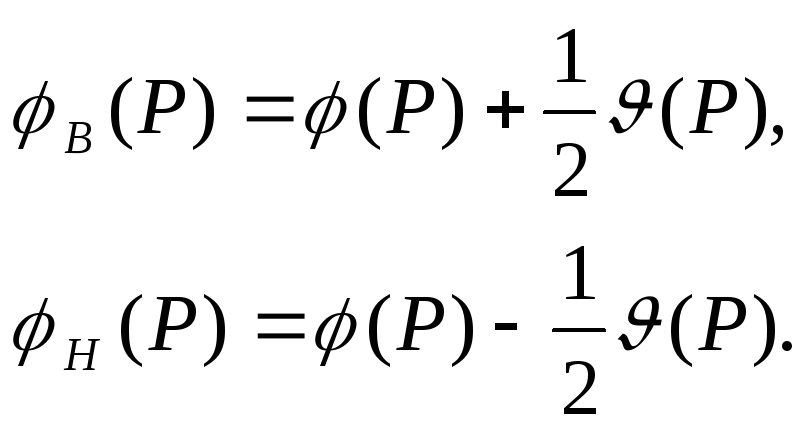 (4.62)
Здесь
(4.62)
Здесь
![]() - предельное значение потенциала двойного
слоя при подходе к точке
- предельное значение потенциала двойного
слоя при подходе к точке
![]() с внутренней стороны, а
с внутренней стороны, а
![]() - предельное значение с наружной стороны.
- предельное значение с наружной стороны.
В отличие от
потенциала двойного слоя потенциал
простого слоя разрыв на поверхности
![]() не испытывает, однако терпит разрыв
производная на нормали:
не испытывает, однако терпит разрыв
производная на нормали:
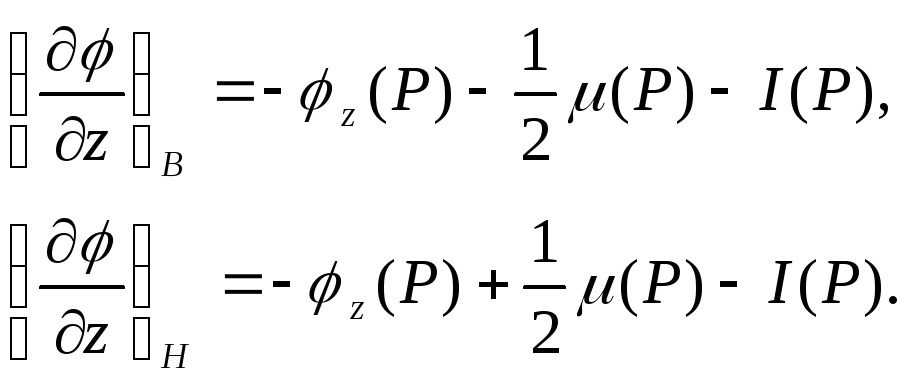 (4.63)
Здесь
(4.63)
Здесь
![]() - поверхностная плотность заряда, а
- поверхностная плотность заряда, а
![]() - интеграл вида:
- интеграл вида:
![]()
где
![]() - плотность дипольного момента в некоторой
фиксированной точке
- плотность дипольного момента в некоторой
фиксированной точке
![]() ,
принадлежащей поверхности
,
принадлежащей поверхности
![]() .
.





