f13051

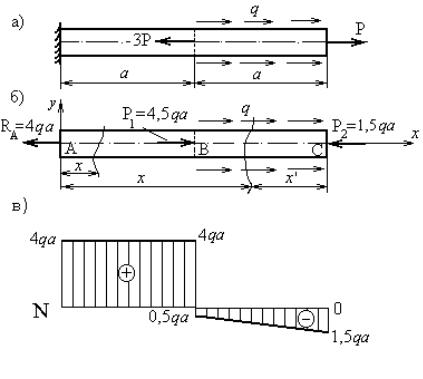
II участок (ВC) a ≤ x ≤ 2a

N = − ∑ X л = − ( − RA + P1 + q ( x − a ) ) = 4 q a − 4,5 q a − q ( x − a ) = = − 0,5 q a − q ( x − a ) − линейный закон .

Так как продольная сила изменяется на втором участке по линейному закону, то для построения эпюры достаточно вычислить значения продольной силы только на границах рассматриваемого участка:

x = a N B = − 0,5 q a − q ( a − a ) = − 0,5 q a ; x = 2 a N C = − 0,5 q a − q ( 2 a − a ) = − 1,5 q a .

При определении продольной силы на втором силовом участке можно рассматривать не левую, а правую отсеченную часть стержня, причем это никак не сказывается на результатах расчета.

II участок (СВ) 0 ≤ x′ ≤ a

N = ∑ X пр = − P2 + q x′ = − 1,5 q a + q x′ − линейный закон ; x′ = 0 N C = − 1,5 qa ;

x′ = a N B = − 1,5 q a + q a = − 0,5 qa .

Эпюра продольных сил, построенная по результатам расчета, показана на рисунке 29в.

Примечание. После построения эпюры продольных сил выполняется проверка ее согласованности с расчетной схемой стержня:

•в сечении стержня, где к нему приложена сосредоточенная сила, эпюра продольных сил должна иметь скачок (разрыв) на величину этой силы;

•если участок стержня не несет никакой распределенной нагрузки

(qx = 0), то продольная сила на этом участке будет постоянной

(N = const);

•если участок стержня загружен равномерно распределенной нагрузкой

(qx = const), то эпюра продольных сил на данном участке будет пред- ставлять собой наклонную прямую, для построения которой доста- точно подсчитать значения продольной силы на концах участка;

•наклон эпюры продольных сил будет тем круче, чем больше величина интенсивности распределенной нагрузки qx;

•если на участке стержня действует равномерно распределенная

нагрузка с интенсивностью qx < 0 (нагрузка направлена в сторону противоположную оси X), то продольная сила на данном участке в соответствии с дифференциальной зависимостью (4.2) слева на-

право возрастает и наоборот, если qx > 0, продольная сила слева направо будет убывать.

Рисунок 29 – К задаче 1: а – заданная схема стержня; б – расчетная схема стержня;

в– эпюра продольных сил

4.3.Задача 2. Скручиваемый стержень

Пример выполнения этого задания приведен в п.3.3 данного пособия.

4.4. Задача 3. Консольная балка

Примечание. Стержень, испытывающий изгиб, называется балкой.

Заданная для расчета схема балки показана на рисунке 30а.

Отбросим жесткую заделку в сечении С, заменив ее действие горизон-

тальной RС′ , вертикальной RС реакциями и реактивным моментом C .

Расчетная схема балки показана на рисунке 30б.

Примечание. График, показывающий, как изменяется интенсивность распределенной нагрузки по длине стержня, называется эпюрой нагрузки.

Равнодействующая равномерно распределенной поперечной нагрузки (qy = const) определяется как площадь эпюры нагрузки (площадь прямо-

угольника), т. е. равна произведению интенсивности этой нагрузки на длину ее действия. Точкой приложения равнодействующей равномерно распределенной нагрузки является центр тяжести эпюры нагрузки, т. е. центр тяжести прямоугольника.

Найдем реакции опор из условий равновесия балки.

Так как по результатам расчета значение реакции RC получилось отрицательным, то на расчетной схеме балки (рисунок 30б) ее направление изменяем на противоположное, а значение реакции подписываем по модулю.

Примечание. После определения опорных реакций обязательно выпол- няется проверка правильности их расчета. Для проверки составляются уравнения равновесия, которые не использовались при вычислении реакций.

Для определения поперечной силы и изгибающего момента в сечениях заданной балки используем метод сечений. В рассматриваемой консольной балке можно выделить два силовых участка.

I участок (АВ) 0 ≤ x ≤ a

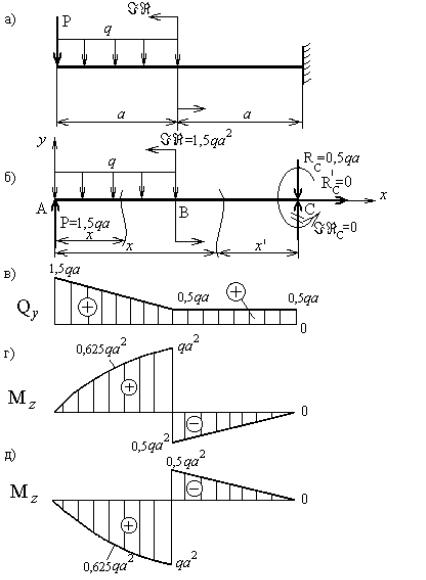
Рисунок 30 – К задаче 3: а – заданная схема балки; б – расчетная схема балки;

в– эпюра поперечных сил; г – эпюра изгибающих моментов для студентов механических специальностей; д – эпюра изгибающих моментов для студентов гидротехнической

специальности

Так как изгибающий момент на данном участке изменяется по закону квадратичной параболы, то для более точного построения его эпюры рассчитаем значения изгибающего момента в трех точках, принадлежащих рассматриваемому участку:

При построении эпюр внутренних усилий на втором силовом участке (ВС) можно рассматривать не левую, а правую отсеченную часть стержня, причем это никак не сказывается на результатах расчета.

II участок (СВ) 0 ≤ x′ ≤ a

Поперечная сила:

Qy = − ∑Y пр = − ( − RC ) = 0,5 q a = const .

Изгибающий момент:

M z = − ∑mzпр = − ( RC x′ − C ) = − 0,5 q a x′ − линейный закон.

Его значения на границах участка:

x′ = 0 M zC = 0 ; x′ = a M zB = − 0,5 q a à = − 0,5 q a2 .

Эпюры поперечных сил и изгибающих моментов, построенные по результатам расчетов для студентов механических специальностей, показаны на рисунках 30в и 30г соответственно, а для студентов гидротехнической специальности эпюра поперечных сил показана на рисунке 30в, а эпюра изгибающих моментов – на рисунке 30д.

Примечание. После построения эпюр поперечных сил и изгибающих

моментов следует проверить их согласованность с расчетной схемой и между собой, используя для этого дифференциальные зависимости (4.2):

•если участок стержня не несет никакой поперечной распределенной

нагрузки (qy = 0), то на этом участке поперечная сила постоянна (Qy = const), а изгибающий момент изменяется по линейному закону; в

частности при Qy = 0 – изгибающий момент будет оставаться по-

стоянным (Mz = const);

•если участок загружен равномерно распределенной поперечной нагруз-

кой (qy = const), то поперечная сила изменяется по линейному закону, а эпюра изгибающих моментов является параболой второй степени;

•выпуклость эпюры изгибающих моментов направлена в сторону дей- ствия распределенной нагрузки qy – данное свойство относится к

правилу построения эпюры изгибающего момента для студентов гидротехнической специальности;

•выпуклость эпюры изгибающих моментов направлена навстречу действию распределенной нагрузки qy – данное свойство относится

к правилу построения эпюры изгибающего момента для студентов механических специальностей;

•если на участке существует сечение, в котором поперечная сила, из- меняясь непрерывно, например по линейному закону, обращается в ноль, то изгибающий момент в этом сечении будет иметь экстре-

мальное (максимальное или минимальное) значение (mz = 0 для всех вариантов заданий); эпюра изгибающего момента в этом сечении бу- дет иметь горизонтальную касательную;

•в месте разрыва (скачкообразного изменения) интенсивности нагруз-

ки qy эпюра поперечных сил получит излом, а эпюра изгибающих мо- ментов останется плавной линией;

•наклон эпюры поперечных сил (при изменении по линейному закону) будет тем круче, чем больше величина интенсивности распреде- ленной нагрузки qy;

•в сечении балки, где приложена сосредоточенная сила (в том числе и реакция опоры), эпюра поперечных сил будет иметь скачок (разрыв) на величину этой силы;

•если сосредоточенная сила направлена вверх (положительна), то и ска- чок на эпюре поперечных сил будет вверх, если сосредоточенная сила направлена вниз (отрицательна), то и скачек на эпюре будет вниз;

•в сечении балки, где приложена сосредоточенная сила (в том числе и реакция опоры), эпюра изгибающих моментов получает излом в направлении действия этой силы – данное свойство относится к

правилу построения эпюры изгибающего момента для студентов гидротехнической специальности;

•в сечении балки, где приложена сосредоточенная (в том числе и реак- ция опоры), эпюра изгибающих моментов получает излом в направле-

нии навстречу действию этой силы – данное свойство относится к

правилу построения эпюры изгибающего момента для студентов механических специальностей;

•в сечении балки, где приложен сосредоточенный момент (в том числе и реактивный) на эпюре изгибающих моментов будет скачок (разрыв) на величину этого момента, а эпюра поперечных сил останется плав- ной непрерывной линией;

•если сосредоточенный момент направлен против часовой стрелки (отрицателен), то скачок на эпюре изгибающих моментов будет вниз; если сосредоточенный момент действует по часовой стрелке (положителен), то скачек будет вверх – данное свойство относится

к правилу построения эпюры изгибающего момента для студентов механических специальностей;

•если сосредоточенный момент направлен против часовой стрелки (отрицателен), то скачок на эпюре изгибающих моментов будет вверх; если сосредоточенный момент действует по часовой стрелке (положителен), то скачек будет вниз – данное свойство относится к

правилу построения эпюры изгибающего момента для студентов гидротехнической специальности;

•в сечении на свободном или шарнирно опертом конце балки изги- бающий момент равен нулю, если в этом сечении не приложен со- средоточенный момент;

•если на свободном или шарнирно опертом конце балки приложен со- средоточенный момент, то изгибающий момент в данном сечении равен по величине этому моменту.

4.5. Задача 4. Двухопорная балка с равномерно распределенной по длине нагрузкой

Заданная схема балки показана на рисунок 31а.

Отбросим опоры и заменим их действие реакциями R A , RB и RB′ ,

которые найдем из условий равновесия балки. Расчетная схема балки показана на рисунке 31б.

Для определения поперечной силы и изгибающего момента в сечениях заданной балки используем метод сечений. В рассматриваемой двухопорной балке можно выделить два силовых участка.

I участок (АВ) 0 ≤ x ≤ 2a

квадратичный закон.

Так как изгибающий момент на данном участке изменяется по закону квадратичной параболы, то для более точного построения его эпюры рассчитаем значения изгибающего момента в трех точках, принадлежащих рассматриваемому участку.

Значения изгибающего момента на границах участка: x = 0 M zA = 1,5 q a 2 ;

x = 2 a M zB = 1,5 q a 2 + 3,75 q a 2 a − 3 q (2 a )2 = − 3 q a 2 .

Примечание. Если на рассматриваемом участке балки существует сечение, в котором поперечная сила, изменяясь непрерывно, обращается в ноль, то в соответствии с дифференциальной зависимостью (4.2) между изгибающим моментом и поперечной силой, в этом сечении изгибающий момент будет иметь экстремальное значение (максимум или минимум). Эпюра изгибающего момента в этом сечении будет иметь горизонталь- ную касательную. Поэтому при построении эпюр внутренних усилий на таком участке в обязательном порядке должны быть рассчитаны коор- динаты экстремума (его абсцисса и ордината).

Для определения абсциссы экстремума (x0) необходимо взять первую производную от выражения для изгибающего момента на рассматривае-

мом участке и приравнять ее к нулю, а затем из полученного уравнения найти координату x0 (абсциссу экстремума). Однако, для определения абсциссы экстремума можно не брать производную от изгибающего мо- мента, а приравнять к нулю выражение для поперечной силы на данном участке (в случае отсутствия на участке распределенного момента mz).

Для определения ординаты экстремума, полученное значение x0 необхо- димо подставить в выражение для изгибающего момента на этом участке.

Так как изгибающий момент на данном участке изменяется по закону квадратичной параболы, то для более точного построения его эпюры рассчитаем значения изгибающего момента в трех точках, принадлежащих рассматриваемому участку:

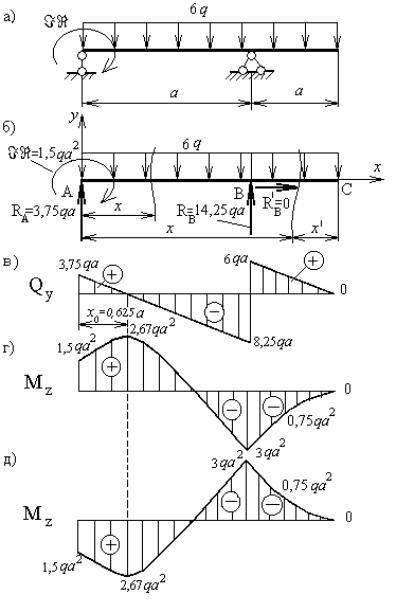
эпюра изгибающих моментов в точке С имеет горизонтальную касательную. Эпюры поперечных сил и изгибающих моментов, построенные по результатам расчетов для студентов механических специальностей, показаны на рисунках 31в и 31г соответственно, а для студентов гидротехнической специальности эпюра поперечных сил показана на рисунке 31в, а

эпюра изгибающих моментов – на рисунке 31д.

Примечание. После построения эпюр поперечных сил и изгибающих

моментов следует проверить их согласованность с расчетной схемой и между собой (см. п. 4.4).

Рисунок 31 – К задаче 4: а – заданная схема балки; б – расчетная схема балки; в – эпюра поперечных сил; г – эпюра изгибающих моментов для студентов механических

специальностей; д – эпюра изгибающих моментов для студентов гидротехнической специальности

4.6. Задача 5. Двухопорная симметрично устроенная балка

Заданная для расчета схема симметрично устроенной балки показана на рисунке 32а. Отбросим опоры и заменим их действие реакциями

RA′ , RA и RB . Расчетная схема балки показана на рисунке 32б.

Примечание. Для симметрично устроенных балок, загруженных сим- метричной относительно середины балки нагрузкой, опорные реакции RA и RB равны по величине и одинаковы по направлению, поэтому можно обозначить RA = RB = R и найти эти реакции опор из уравнения равновесия ∑Y = 0 .

Для симметрично устроенных балок, загруженных антисимметрич- ной относительно середины балки нагрузкой, опорные реакции RA и RB равны по величине и противоположны по направлению, поэтому для опре- деления этих опорных реакций следует воспользоваться уравнениями рав- новесия ∑ M A = 0 и ∑ M B = 0 , и выполнить проверку с помощью урав-

нения равновесия ∑Y = 0 .

Так как данная балка симметрично устроена и загружена симметричной относительно середины балки нагрузкой, то обозначим RA = RB = R и найдем реакции опор из условий равновесия балки.

∑ X = 0 ; RA′ = 0 .

Для определения поперечной силы и изгибающего момента в сечениях заданной балки используем метод сечений. В рассматриваемой двухопорной балке можно выделить три силовых участка.

I участок (АС) 0 ≤ x ≤ a

Поперечная сила:

Qy = ∑Y л = RA = 2 q a = const .

Изгибающий момент:

M z = ∑mzл = RA x = 2 q a x − линейный закон .

Его значения на границах участка:

II участок (СD) a ≤ x ≤ 2a

Поперечная сила:

Qy = ∑Y л = RA − P − q ( x − a ) = 2 q a − 1,5 q a − q ( x − a ) =

= 0,5 q a − q ( x − a ) − линейный закон.

Ее значения на границах участка:

квадратичный закон .

Значения изгибающего момента на границах участка:

Так как на рассматриваемом силовом участке существует сечение, в котором поперечная сила, изменяясь непрерывно, обращается в ноль, то изгибающий момент в этом сечении будет иметь экстремальное значение.

Расчет абсциссы и ординаты экстремума:

x′ = 0 M zB = 0 ; x′ = а M zD = 2 q a2 .

Эпюры поперечных сил и изгибающих моментов, построенные по результатам расчетов для студентов механических специальностей, показаны на рисунках 32в и 32г соответственно, а для студентов гидротехнической специальности эпюра поперечных сил показана на рисунке 32в, а эпюра изгибающих моментов – на рисунке 32д.

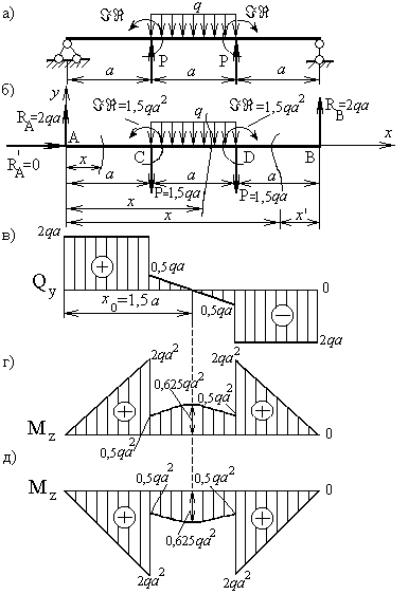
Рисунок 32 – К задаче 5: а – заданная схема балки; б – расчетная схема балки; в – эпюра поперечных сил; г – эпюра изгибающих моментов для студентов механических

специальностей; д – эпюра изгибающих моментов для студентов гидротехнической специальности

∑ M B = 0 ; − Q 23 3 a + RA 3 a − P1 a = 0 ;

1,5 q a 2 a + 0,5 q a a R A = 3 a

Проверка:

∑Y = 0 ; RA − Q − RB + P1 = 0 ;

1,17 q a − 1,5 q a − 0,17 q a + 0,5 q a = 0 ; 0 ≡ 0 .

Для определения поперечной силы и изгибающего момента в сечениях заданной балки используем метод сечений. В рассматриваемой двухопорной балке можно выделить два силовых участка.

I участок (CВ) 0 ≤ x′ ≤ a

Поперечная сила:

Qy = − ∑Y пр = − ( P1 ) = − 0,5q a = const .

Изгибающий момент:

M z = − ∑mzпр = − ( − P1 x′ ) = 0,5 q a x′ − линейный закон .

Его значения на границах участка:

Примечание. При определении внутренних усилий на участках балки, где действует распределенная по закону «треугольника» нагрузка, следу- ет рассматривать ту отсеченную часть, где находится вершина тре- угольника (точка, где qy = 0):

•если вершина треугольника находится справа от рассматриваемого сечения, то внутренние усилия подсчитывают, рассматривая правую отсеченную часть балки;

•если вершина треугольника находится слева от рассматриваемого сечения, то внутренние усилия подсчитывают, рассматривая левую отсеченную часть балки.

На участке ВА балки действует распределенная по закону «треугольника» нагрузка с вершиной справа, от проведенного на участке сечения, поэтому будем рассматривать правую отсеченную часть.

II участок (ВА) a ≤ x′ ≤ 4a

Поперечная сила:

Q y = −∑Y пр = − ( P1 − RB − Q( x′ )) ;

где Q(x´) – равнодействующая отсеченной части распределенной нагрузки.

Примечание. Равнодействующая отсеченной части распределенной по закону «треугольника» нагрузки Q(x) определяется из подобия тре- угольников, представляющих эпюру всей «треугольной» нагрузки и эпюру отсеченной ее части (рисунок 33).

Здесь L – длина всей «треугольной» нагрузки;

x – длина отсеченной части «треугольной» нагрузки.

Тогда из подобия треугольников, представляющих эпюру всей распределенной нагрузки на рассматриваемом участке балки и эпюру ее отсекаемой части, можно получить выражение для вычисления равнодействующей отсеченной части нагрузки Q(x′):

квадратичный закон .

Так как поперечная сила на данном участке изменяется по закону квадратичной параболы, то для более точного построения ее эпюры рас-

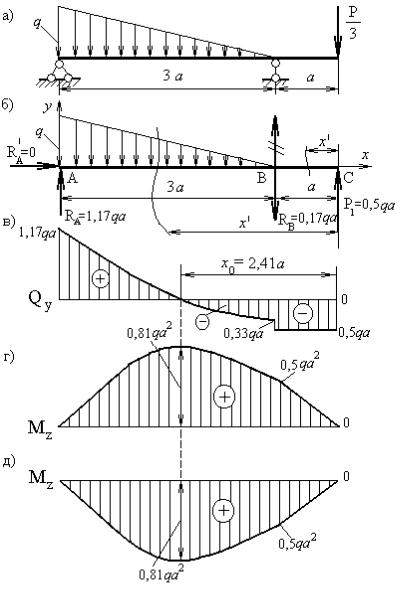
считаем значения поперечной силы в трех точках, принадлежащих рассматриваемому участку:

Примечание. В соответствии с дифференциальной зависимостью (4.2) функция поперечной силы Qy, изменяющаяся по квадратичному закону, име- ет экстремум в точке, где qy = 0 (т. е. под вершиной треугольника). В этой точке эпюра поперечных сил будет иметь горизонтальную касательную.

Так как изгибающий момент на данном участке изменяется по закону кубической параболы, то для более точного построения его эпюры рассчитаем значения изгибающего момента в трех точках, принадлежащих рассматриваемому участку. Его значения на границах участка:

Так как на рассматриваемом силовом участке существует сечение, в котором поперечная сила, изменяясь непрерывно, обращается в ноль, то изгибающий момент в этом сечении будет иметь экстремальное значение.

Примечание. При определении абсциссы экстремума на участке бал- ки с «треугольной» нагрузкой необходимо решить квадратное уравнение,

причем из двух корней этого уравнения только один будет удовлетворять условиям задачи. Значение абсциссы экстремума x0 обязательно должно быть положительным и принадлежать рассматриваемому участку.

Рисунок 34 – К задаче 6: а – заданная схема балки; б – расчетная схема балки; в – эпюра поперечных сил; г – эпюра изгибающих моментов для студентов механических

специальностей; д – эпюра изгибающих моментов для студентов гидротехнической специальности

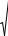
Расчет абсциссы и ординаты экстремума:

= 0,81 q a 2 .

Эпюры поперечных сил и изгибающих моментов, построенные по результатам расчетов для студентов механических специальностей, показаны на рисунках 34в и 34г соответственно, а для студентов гидротехнической специальности эпюра поперечных сил показана на рисунке 34в, а эпюра изгибающих моментов – на рисунке 34д.

Примечание. После построения эпюр поперечных сил и изгибающих

моментов следует проверить их согласованность с расчетной схемой и между собой (см. п. 4.4). Для балки, нагруженной распределенной по зако- ну «треугольника» нагрузкой следует обратить внимание на следующие особенности. Если на участке действует распределенная по закону «тре- угольника» поперечная нагрузка qy, то:

•функция поперечной силы Qy изменяется по квадратичному закону и имеет экстремум в точке, где qy = 0 (т. е. под вершиной треугольни- ка), а эпюра срезывающих сил в этой точке будет иметь горизон- тальную касательную;

•эпюра изгибающих моментов является параболой третьей степени;

•выпуклость эпюры изгибающих моментов направлена в сторону дей- ствия распределенной нагрузки qy – данное свойство относится к

правилу построения эпюры изгибающего момента для студентов гидротехнической специальности;

•выпуклость эпюры изгибающих моментов направлена навстречу действию распределенной нагрузки qy – данное свойство относится

к правилу построения эпюры изгибающего момента для студентов механических специальностей.

4.8. Задача 7. Балка с шарниром

Заданная схема балки показана на рисунке 35а. Заданная система состоит из двух стержней, соединенных между собой шарниром.

Отбросим опоры и заменим их действие реактивными усилиями

RA′ , RA , A , RC . Расчетная схема балки показана на рисунке 35б.

Неизвестными являются четыре усилия, для определения которых можно составить только три уравнений равновесия. Так как в сечении В балка имеет шарнир, где изгибающий момент равен нулю, то для этого сечения можно составить дополнительное уравнение:

M zB = −∑mzпр = − (− RC 2 a + q 2 a a) = 0 ; RC = q a .

Остальные реактивные усилия найдем из условий равновесия балки.

I участок (АE) 0 ≤ x ≤ 0,5 a