f13051

Рисунок 24 – К задаче 5: а – заданная схема балки; б – расчетная схема балки; в – эпюра срезывающих сил; г – эпюра изгибающих моментов

Расчет абсциссы и ординаты экстремума:

= − 0,625 q a2 .

III участок (BD) 0 ≤ x′ ≤ a

Срезывающая сила:

Vz = − ∑ Z пр = − ( RВ ) = − (− 2 q a) = 2 q a = const .

Изгибающий момент:

M y = −∑ M прy = − RВ x′ = − 2 q a x′ − линейный закон.

Его значения на границах участка: x′ = 0 M yB = 0 ; x′ = а M yD = −2 q a2 .

Эпюры срезывающих сил и изгибающих моментов, построенные по результатам расчетов, показаны на рисунках 24в и 24г соответственно.

Примечание. После построения эпюр срезывающих сил и изгибающих

моментов следует проверить их согласованность с расчетной схемой и между собой (см. п. 3.4). Для симметрично устроенных балок и загру- женных симметричной или антисимметричной нагрузкой следует обра- тить внимание на следующие особенности:

•при симметричной нагрузке у симметрично устроенной балки эпюра

срезывающих сил антисимметрична относительно середины балки (срезывающие силы в симметричных сечениях равны по величине и имеют противоположные знаки), а эпюра изгибающих моментов – симметрична;

•при антисимметричной нагрузке, наоборот, – эпюра срезывающих сил симметрична, а эпюра изгибающих моментов – антисимметрич- на относительно середины балки.

3.7. Задача 6. Двухопорная балка с распределенной нагрузкой, изменяющейся по линейному закону

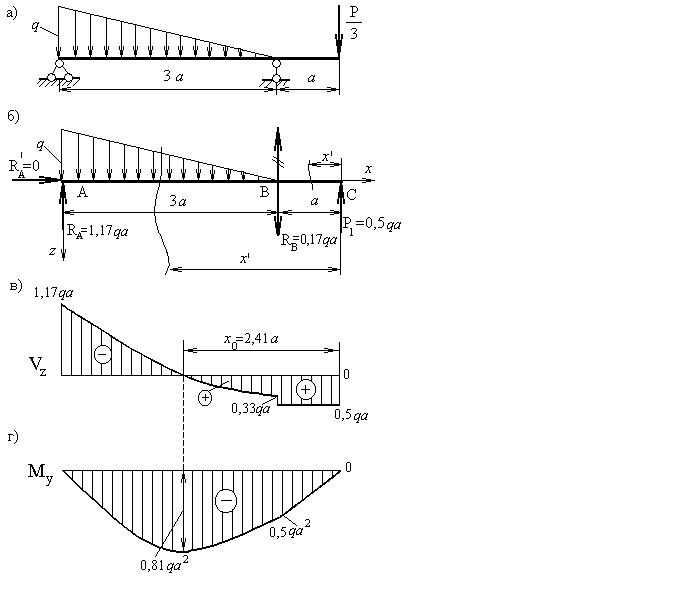
Заданная схема балки показана на рисунке 26а.

Отбросим опоры и заменим их действие реакциями RA , RA′ и RB .

Расчетная схема балки показана на рисунке 26б.

Примечание. Равнодействующая распределенной по закону «тре- угольника» поперечной нагрузки qz определяется как площадь эпюры на- грузки (площадь треугольника). Точкой приложения равнодействующей распределенной нагрузки является центр тяжести эпюры нагрузки, т. е. центр тяжести треугольника.

Найдем реакции опор из условий равновесия балки.

∑ X = 0 ; RA′ = 0 .

∑ M A = 0 ; − Q 13 3 a + RB 3 a + P1 4 a = 0 ;

1

где Q = 2 q 3 a = 1,5 q a – равнодействующая всей «треугольной» нагрузки.

Так как по результатам расчета значение реакции RB получилось отрицательным, то на расчетной схеме балки (рисунок 26б) ее направление изменяем на противоположное, а значение реакции подписываем по модулю.

Для определения срезывающей силы и изгибающего момента в сечениях заданной балки используем метод сечений. В рассматриваемой двухопорной балке можно выделить два силовых участка.

I участок (CВ) 0 ≤ x′ ≤ a

Срезывающая сила:

Vz = − ∑Zпр = − (− P1 ) = 0,5 q a = const .

Изгибающий момент:

M y = −∑ M прy = − ( P1 x′ ) = − 0,5 q a x′ − линейный закон .

Его значения на границах участках: x′ = 0 M Cy = 0 ;

x′ = a M yB = − 0,5 q a a = − 0,5 q a2 .

Примечание. При определении внутренних усилий на участках балки, где действует распределенная по закону «треугольника» нагрузка, следу- ет рассматривать ту отсеченную часть, где находится вершина тре- угольника (точка, где qz = 0):

•если вершина треугольника находится справа от рассматриваемого сечения, то внутренние усилия подсчитывают, рассматривая правую отсеченную часть балки;

•если вершина треугольника находится слева от рассматриваемого сечения, то внутренние усилия подсчитывают, рассматривая левую отсеченную часть балки.

На участке BА балки действует распределенная по закону «треугольника» нагрузка с вершиной справа, от проведенного на участке сечения, поэтому будем рассматривать правую отсеченную часть.

II участок (ВА) a ≤ x′ ≤ 4a

Срезывающая сила:

Vz = − ∑ Z л = − ( − P1 + RB + Q ( x′)) ;

где Q(x′) – равнодействующая отсеченной части распределенной нагрузки.

Примечание. Равнодействующая отсеченной части распределенной по закону «треугольника» нагрузки Q(x) определяется из подобия тре- угольников, представляющих эпюру всей «треугольной» нагрузки и эпюру отсеченной ее части (рисунок 25).

Или через площади подобных треугольников:

Здесь L – длина всей «треугольной» нагрузки;

x – длина отсеченной части «треугольной» нагрузки.

Тогда из подобия треугольников, представляющих эпюру всей распределенной нагрузки на рассматриваемом участке балки и эпюру ее отсекаемой части, можно получить выражение для вычисления равнодействующей отсеченной части нагрузки Q(x′):

квадратичный закон.

Так как срезывающая сила на данном участке изменяется по закону квадратичной параболы, то для более точного построения ее эпюры рассчитаем значения срезывающей силы в трех точках, принадлежащих рассматриваемому участку.

Примечание. В соответствии с дифференциальной зависимостью (3.2) функция срезывающей силы Vz, изменяющаяся по квадратичному закону, имеет экстремум в точке, где qz = 0 (т. е. под вершиной тре- угольника). В этой точке эпюра срезывающих сил будет иметь горизон- тальную касательную.

Так как на рассматриваемом силовом участке существует сечение, в котором срезывающая сила, изменяясь непрерывно, обращается в ноль, то изгибающий момент в этом сечении будет иметь экстремальное значение.

Примечание. При определении абсциссы экстремума на участке бал- ки с «треугольной» нагрузкой необходимо решить квадратное уравнение,

причем из двух корней этого уравнения только один будет удовлетворять условиям задачи. Значение абсциссы экстремума x0 обязательно должно быть положительным и принадлежать рассматриваемому участку.

Расчет абсциссы и ординаты экстремума:

Эпюры срезывающих сил и изгибающих моментов, построенные по результатам расчетов, показаны на рисунках 26в и 26г соответственно.

Примечание. После построения эпюр срезывающих сил и изгибающих

моментов следует проверить их согласованность с расчетной схемой и между собой (см. п. 3.4). Для балки, нагруженной распределенной по зако- ну «треугольника» поперечной нагрузкой следует обратить внимание на следующие особенности. Если на участке действует распределенная по закону «треугольника» поперечная нагрузка qz, то:

•функция срезывающей силы Vz изменяется по квадратичному закону и имеет экстремум в точке, где qz = 0 (т. е. под вершиной треугольни- ка), а эпюра срезывающих сил в этой точке будет иметь горизон- тальную касательную;

•эпюра изгибающих моментов является параболой третьей степени,

обращенной выпуклостью вниз при qz > 0 и выпуклостью вверх при qz < 0, следовательно, выпуклость эпюры изгибающих моментов на- правлена в сторону действия распределенной нагрузки qz.

Рисунок 26 – К задаче 6: а – заданная схема балки; б – расчетная схема балки; в – эпюра срезывающих сил; г – эпюра изгибающих моментов

3.8. Задача 7. Балка с шарниром

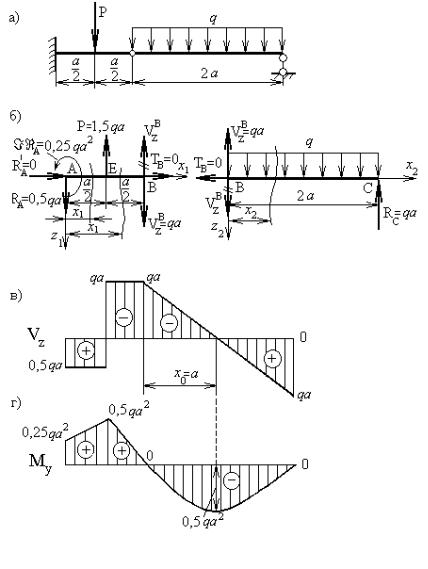
Заданная схема балки показана на рисунке 27а. Заданная система состоит из двух стержней, соединенных между собой шарниром.

Отбросим опоры и шарнир, разделив, тем самым, стержневую систему на отдельные стержни. Покажем реакции всех отброшенных нами связей на расчетной схеме балки (рисунок 27б). Шарнир момента не передает,

поэтому в сечении, где стоит шарнир, в нашем примере это сечение В,

действует лишь срезывающая сила VzB и осевая сила TB . Силы VzB и TB

являются силами взаимодействия стержней между собой, поэтому пока- зывая их приложенными к стержням, их направляют в противоположные стороны. На рисунке 27б силы взаимодействия показаны положительными.

Неизвестны шесть усилий: RA , RA′ , A , VzB , TB , RC , для их опреде-

ления можно составить шесть уравнений равновесия (по три для каждого стержня).

Для определения величин опорных реакций и внутренних усилий вве-

дем для каждого стержня собственную (местную) систему координат:

для первого стержня – это оси X1Z1, для второго – X2Z2.

Примечание. При выборе местной системы координат ее начало следует располагать на левом конце рассматриваемого стержня; ось Xi

Из уравнения (3.4) получаем R A = 1,5 q a + VzB = 1,5 q a − qa = 0,5 q a ,

а из уравнения (3.5):

A = − 1,5 q a 0,5 a − VzB a = − 1,5 q a 0,5 a + q a a = 0,25 q a2 .

Так как при вычислении усилия V zB его значение получилось отрица-

тельным, то на расчетных схемах стержней (рисунок 27б) направление данного усилия изменяем на противоположное, а значение подписываем по модулю.

Так как внешних продольных сил на заданной схеме нет, то в обоих стержнях осевых сил тоже нет.

Первый стержень (AB) I участок (АE) 0 ≤ x1 ≤ 0,5 a

Срезывающая сила:

Vz = ∑ Z1л = RA = 0,5 q a = const .

Изгибающий момент:

M y = ∑ M лy = A + RA x1 = 0,25 q a 2 + 0,5 q a x1 − линейный закон .

Его значения на границах участка: x1 = 0 M yA = 0,25 q a2 ;

x1 = 0,5 а M yE = 0,25 q a2 + 0,5 q a 0,5 а = 0,5 q a2 . II участок (ЕВ) 0,5 a ≤ x1 ≤ a

Срезывающая сила:

Vz = ∑ Z 1л = RA − P = 0,5 q a − 1,5 q a = − q a = const .

Изгибающий момент:

M y = ∑ M лy = A + R A x1 − P ( x1 − 0,5 а ) ;

Второй стержень (BС)

В данном стержне только один силовой участок: 0 ≤ x2 ≤ 2a

Срезывающая сила:

Vz = ∑ Z 2л = − VzB + q x2 = − q a + q x2 − линейный закон.

Ее значения на границах участка:

закон.

Так как изгибающий момент в стержне BC изменяется по закону квадратичной параболы, то для более точного построения его эпюры рассчитаем значения изгибающего момента в трех точках, принадлежащих рассматриваемому участку. Его значения на границах участка:

Примечание. Равенство M yB = 0 является для рассматриваемой бал-

ки контрольным, так как изгибающий момент в шарнире должен быть равен нулю.

Так как на рассматриваемом силовом участке стержня существует сечение, в котором срезывающая сила, изменяясь непрерывно, обращается в ноль, то изгибающий момент в этом сечении будет иметь экстремальное значение.

Расчет абсциссы и ординаты экстремума:

Эпюры срезывающих сил и изгибающих моментов, построенные по результатам расчетов, показаны на рисунках 27в и 27г соответственно.

Примечание. После построения эпюр срезывающих сил и изгибающих

моментов следует проверить их согласованность с расчетной схемой и между собой, при этом для балок с шарниром все дифференциальные за-

висимости (3.2), а, следовательно, и особенности эпюр остаются таки- ми же (без изменения), как и для балок без шарнира (см. п. 3.4). Однако

для балок с шарниром следует обратить внимание на следующие особен- ности. Если в сечении, где стоит шарнир, не приложены ни сосредото- ченная сила, ни сосредоточенный момент, то:

•на эпюре срезывающих сил и на эпюре изгибающих моментов в сече- нии, где стоит шарнир, не должно быть скачков (разрывов);

•изгибающий момент в сечении, где стоит шарнир, обязательно дол- жен быть равен нулю;

•в сечении, где стоит шарнир, на эпюре изгибающих моментов не должно быть излома.

Рисунок 27 – К задаче 7: а – заданная схема балки; б – расчетная схема балки; в – эпюра срезывающих сил; г – эпюра изгибающих моментов

3.9. Задача 8. Плоская рама

Примечание. Для рамы вводится понятие узла – это точка, в кото- рой соединяются стержни рамы. Стержни в узлах рамы соединяются жестко, в результате такого соединения в узле возникают внутренние усилия: осевая и срезывающая силы, изгибающий момент.

Если в каждом узле рамы соединяется не более двух стержней, рама называется простой, если хотя бы в одном узле соединяется более двух стержней – рама называется сложной. В данном задании рассматрива- ются только простые рамы.

Заданную простую раму, показанную на рисунке 28а, можно рассматривать как один ломаный стержень, поэтому для определения опорных реакций можно составить три уравнения равновесия. Отбросим опоры и заме-

ним их действие реакциями RA , RA′ , RE . При определении опорных реак-

ций используется общая система координат – XZ, ось X которой направлена слева направо, ось Z – вниз. Расчетная схема рамы показана на рисунке 28б.

Найдем реакции опор из условий равновесия рамы.

∑M A = 0 ; − P1 2 a − q 2 a a + RE′ 2 a + 1 = 0 ;

− 2 q a 2 a + 0,5 q a 4 a + 2 q a 2 a + 2 q a 2 − 2,5 q a 2 a + q a 2 = 0 ; − 9 q a 2 + 9 q a 2 = 0 0 ≡ 0 .

Для построения эпюр внутренних усилий в каждом стержне выбира- ем местную систему координат – XiZi.

Примечание. При определении внутренних усилий, действующих в се- чениях стержней рамы, и построении их эпюр следует обратить внима- ние на следующие особенности:

•оси местной системы координат каждого стержня направляют та- ким образом, чтобы, развернув все стержни рамы в одну горизонталь-

ную линию, местная система координат каждого стержня совпала бы по направлению с общей системой координат; при этом ось Xi всегда должна быть направлена вдоль оси рассматриваемого стержня;

•если i-ый стержень мысленно повернуть так, чтобы он занял гори-

зонтальное положение, ось Xi должна быть направлена слева напра- во, а Zi – вниз; для такого положения координатных осей и определя- ются понятия, используемые при расчете внутренних усилий – «пра- вая отсеченная часть», «отсеченная левая часть», а также при по- строении эпюр – «верх», «низ»;

•при построении эпюры изгибающего момента его значения следует откладывать строго со стороны растянутых волокон стержня;

•при определении внутренних усилий, действующих в поперечных сече- ниях стержней рамы, используется метод сечений, при этом длина отсеченной части измеряется только в пределах длины рассматри- ваемого стержня;

•так как стержни в узлах рамы соединяются жестко, то при опреде- лении внутренних усилий учитываются все внешние усилия, прило- женные не только к рассматриваемому стержню, но и к другим стержням рамы, расположенным левее или правее сечения, в зависи- мости от того, какая отсеченная часть стержня рассматривается;

•эпюры внутренних усилий изображают каждую на отдельном кон- туре рамы и располагают рядом на одном листе.

Рассмотрим построение эпюр внутренних усилий для заданной рамы.

Первый стержень (АВ) I участок (AВ) 0 ≤ x 1 ≤ 2 a

Осевая сила:

T = − ∑ X 1л = − ( RA ) = − 2 q a = const .

Срезывающая сила:

Vz = ∑Z1л = RA′ = 0,5 q a = const .

Изгибающий момент:

M y = ∑M лy = R A′ x1 = 0,5 q a x1 − линейный закон.

Его значения на границах участка:

Срезывающая сила:

Vz = ∑Z1л = RA′ + P1 = 0,5 q a + 2 q a = 2,5 q a = const .

Изгибающий момент:

M y = ∑M лy = RA′ x1 + P1 ( x1 − 2 a ) = 0,5 q a x1 + 2 q a ( x1 − 2 a ) −

линейный закон.

Его значения на границах участка: x1 = 2 a M yE = 0,5 q a 2 а = q a2 ;

x1 = 4 a M yB = 0,5 q a 4 a + 2 q a ( 4 a − 2 a ) = 6 q a2 .

Для определения внутренних усилий в стержнях СD и DE удобнее рассматривать «правую отсеченную часть», так как выражения для внутренних усилий в этом случае будут иметь более простой вид. На каждом из этих стержней будет всего по одному силовому участку.

Осевая сила:

T = ∑ X пр2 = − RE′ = − 2,5 q a .

Срезывающая сила:

Изгибающий момент:

квадратичный закон .

Так как изгибающий момент на данном участке изменяется по закону квадратичной параболы, то для более точного построения его эпюры рассчитаем значения изгибающего момента в трех точках, принадлежащих рассматриваемому участку:

ным, а эпюра изгибающих моментов в точке D имеет касательную, параллельную оси стержня DC.

Эпюры внутренних усилий, построенные по результатам расчета, показаны на рисунках 28в, 28г, 28д.

Примечание. После построения эпюр внутренних усилий следует проверить их согласованность с расчетной схемой и между собой, при этом для стержней рамы сохраняются все дифференциальные зависи- мости (3.2) между внутренними усилиями и внешними силами, как и для прямого стержня (см. п. 3.4). Кроме того, следует обратить внимание на следующие особенности:

•если в узле рамы не приложен сосредоточенный момент, то изги-

бающий момент в конце одного стержня по величине и по знаку равен изгибающему моменту вначале второго стержня, выходящего из этого же узла;

•если в узле рамы приложен сосредоточенный момент, то на эпюре изгибающих моментов в этом узле будет скачок на величину прило- женного момента.

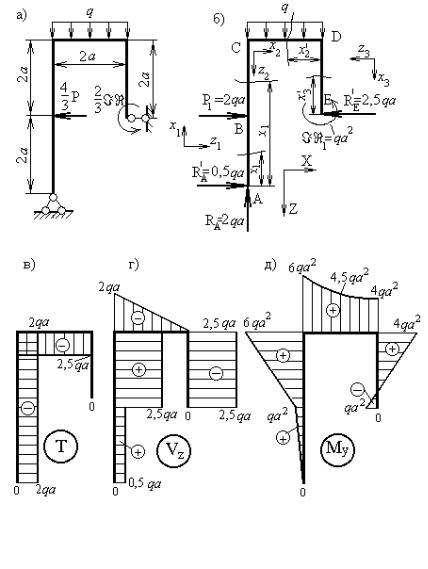
Рисунок 28 – К задаче 8: а – заданная схема рамы; б – расчетная схема рамы; в – эпюра осевых сил; г – эпюра срезывающих сил; д – эпюра изгибающих моментов

4. Пример выполнения задания для студентов гидротехнической и механических специальностей

Построить эпюры внутренних усилий в поперечных сечениях стерж-

сивность распределенной по участку продольной нагрузки q, а в задаче 2 интенсивность распределенного момента m постоянны по длине участка.

4.1. Основные положения для построения эпюр внутренних усилий

Рассмотрим построение эпюр внутренних усилий в прямом стержне в вертикальной плоскости (XY). Напомним правило знаков для внешних и внутренних усилий, действующих в вертикальной плоскости.

Внешние силы будем считать положительными при их действии в сторону положительного направления соответствующих координатных осей, то есть вертикальные силы положительны при направлении их снизу вверх, а горизонтальные – слева направо.

Моменты, как внешние, так и реактивные, создаваемые заделками, положительны при их действии по часовой стрелке, при взгляде в поло- жительное направление координатной оси.

Продольная сила N положительна, когда она вызывает растяжение отсеченной части стержня, и отрицательна, если вызывает ее сжатие.

Поперечная сила Qy , скручивающий момент Mx и изгибающий момент Mz положительны, если при действии на правую отсеченную часть стержня они направлены как положительная внешняя сила и положи- тельный внешний момент, а при действии на левую отсеченную часть – как отрицательные внешняя сила и внешний момент.

Данное правило можно сформулировать также следующим образом:

•скручивающий момент Mx положителен, если, глядя в торец отсечен- ной части стержня, мы видим вращение момента по ходу часовой стрелки;

•поперечная сила Qy считается положительной, если она вращает отсеченную часть стержня по ходу часовой стрелки и отрицатель- ной, если вращение происходит против хода часовой стрелки;

•изгибающий момент положителен, если сжаты верхние волокна отсе-

ченной части стержня, и отрицателен, если сжаты нижние волокна.

Положительные значения продольной и поперечной силы, скручивающего момента следует откладывать вверх, а отрицательные вниз от базовой линии эпюры. Положительные значения изгибающего момента

студенты гидротехнической специальности должны откладывать вниз от базовой линии эпюры, а отрицательные – вверх, то есть значения изгибающего момента откладываются со стороны растянутых волокон стержня. Студентам механических специальностей положительные

значения изгибающего момента следует откладывать вверх от базовой линии эпюры, а отрицательные – вниз, то есть значения изгибающего мо-

мента на эпюре откладываются со стороны сжатых волокон стержня.

Для подсчета внутренних усилий, действующих в поперечном сечении стержня, используются следующие равенства, полученные методом сече- ний из уравнений равновесия отсеченной части стержня:

Здесь ∑ X л , ∑Y л – суммы проекций на оси X и Y всех внешних сил

(включая реакции опор и равнодействующие распределенных усилий), действующих на левую отсеченную часть стержня;

∑mxл , ∑mzл – суммы моментов всех внешних усилий (включая

реактивные, сосредоточенные и распределенные моменты), действующих на левую отсеченную часть стержня, относительно соответствующей координатной оси, проходящей через центр тяжести, рассматриваемого сечения.

В правом столбце выражений (4.1) приведены аналогичные формулы для правой отсеченной части стержня, они отличаются только знаками перед суммами. Причем для одного и того же сечения стержня внутренние усилия, подсчитанные по выражениям для левой и правой отсеченной части, должны давать одинаковый результат.

Дифференциальные зависимости между внутренними и внешними усилиями для прямого стержня имеют вид:

Здесь q x , q y – интенсивность распределенной нагрузки, действую-

щей в направлении координатных осей X и Y соответственно;

mx , mz – интенсивность распределенного момента, действую-

щего относительно координатных осей X и Z соответственно.

Остальные положения, которые используются при построении и проверке правильности эпюр внутренних усилий, приведены в примечаниях к рассмотренным примерам.

4.2. Задача 1. Растянуто-сжатый стержень

Заданная для расчета схема стержня показана на рисунке 29а.

Начинаем решение задачи с определения опорной реакции. Отбросим заделку и заменим ее действие реакцией RА (рисунок 29б). Так как вся внешняя нагрузка, действующая на стержень, состоит только из сил параллельных оси стержня (продольные силы), то и реакция заделки будет состоять только из продольной составляющей (плоскопараллельная система сил).

Примечание. Равнодействующая равномерно распределенной про-

дольной нагрузки равна произведению интенсивности этой нагрузки на длину ее действия.

Из условия равновесия найдем реакцию в заделке RА:

∑ X = 0 ; − RА + P1 + q a − P2 = 0 ;

− RА + 4,5 q a + q a − 1,5 q a = 0 ; RА = 4 q a .

Так как значение реакции получилось положительным, то можно сделать вывод о том, что направление реакции RА на расчетной схеме (рисунок 29б) выбрано верно.

Примечание. Вычисленное значение реакции следует обязательно подписать на расчетной схеме стержня. Если при вычислении опорной реакции ее значение получилось отрицательным, то направление реакции на расчетной схеме следует изменить на противоположное, а значение реакции подписать по модулю.

Для определения продольной силы используем метод сечений. Для заданного стержня можно выделить два силовых участка, в пределах которых закон изменения продольной силы будет неизменным.

I участок (АВ) 0 ≤ x ≤ a N = −∑ X л = − ( − RA ) = 4 q a = const .