
пособие 7 по матану (2 курс)
.pdf¨¬. •.ƒ. —¥à-ë襢᪮£®
….Œ‚.‚. ƒ. 㤮è•à â-订¨ª®¢
ǑŽ ŒǑ•€€…ŒŠ’ˆ€’ˆ—…—‘Šˆ…ŠŽŒ“… ‡€•Ÿ’ˆŸ€•€‹ˆ‡“
— áâì 7
ˆ•’Œ•Ž…ƒ•ˆ•Ž‚ƒˆ• Ǒ…€•ˆ…Œ… …”“•Š••›•–ˆ‰
“祡-®"Œ-¬¥â®â¥¤¨ç¬ â¨ç¥áª¥®áª¨©¥ ¯®á®¡¨- «¨§"¥ ¯® ªãàáã (3 ᥬ¥áâà, ®-â஫ì- ï à ¡®â ü7)
ˆ‡„€’…‹œ‘’‚Ž ‘€•€’Ž‚‘ŠŽ2011 ƒŽ “•ˆ‚…•‘ˆ’…’€
|
ƒã¤®è-¨ª®¢ |
….‚., •à â 订 |
Œ.‚. |
|
|
|||||
ˆ§¤{¢® ‘ ªâ¨çà .äã¥áª¨-{⥠|
, 2011. { 48 |
á. |
⥬ â¨ç¥áª®¬ã |
- «¨§ã. — áâì 7: ˆ-- |
||||||
ƒ |
Ǒà |
|
|
§ -ïâ¨ï ¯® |
|
|||||
⥣à¨à®¢ - |
|
-ªæ¨© ¬-®£¨å ¯¥à¥¬¥--ëå: “祡. |
¯®á®¡¨¥. { ‘ à ⮢: |
|||||||
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
¡¨¨ª¥¤«ï-¥ïâ¯à¨¢®àáâ㤥¤«ï¥®à襥¥â¨ç-¤ïâá-¨ï⮢¬®áâ®ïâ¥áª¨¢ëç¨á«¨âï1-¯®¤à®¡2ᢥ ªãàᮢ,¥«ì¥¤¥-¥-«ì¨ï£à¨§ãç®-¯®àë姮¡à¬¥è¥îé¨å-â--¤¨ï¥¬çë.¨â¨ç¥¬â¯à¨¬Šà®¬¥â¥ªáâë¥áª¬¥¥ |
||||||
|
|
|
|
®®¤ë |
|
|
|
|
|
|
|
|
|
|
â |
|
|
|
|
|
|
|
|
¯à«¨§â¨¯®¢ëç¡®¥¥¤.áç,à-.§ã¯à¨â-¥ªà篮ᬥ-¥- |
|
|
|
|
|
|
||
â¨çàëâ¬ã¥®à-â஫ì॥Ǒ®á®¡¨Ǒ®á®¡¨áª¨©-¥â¨ç諨§ã¥-¥-¨ïáªëå-¥¥ISBN®©¨§á® |
978 5-91879-125-7 |
|
|
|
|
|||||
|
|
|
|
•¥ª ¬¥-¤ãîâ |
¯¥ç |
|
|
|||
|
|
ª 䥤à ⥠ਨ äã-ªæ¨© |
¯à ¡«¨ ¥-¨© |
|
||||||
|
|
|
|
‘ à ⮢᪮£® £®áã-¨¢¥àáâ¨:â¥â |
“„Š 517.262(075.3 ) |
|||||
|
ISBN |
|
|
|
|
|
|
|
|
••Š 22.161ï722 |
|
978-5-91879-125-7 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
1.1. •¥®¡å®¤¨¬ë¥§ ⥮ |
¥â¨ç¥áª¨¥ ᢥ¤¥-¨ï. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• Ǒãáâì ¨¬¥¥âáï ¨-â¥£à « Za |
f (x, y)dx. Ǒ®¢â®à-ë¬ ¨-â¥£à «®¬ - §ë¢ ¥âáï |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
d |
|
|
b |
f x, y dx!dy, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
dy Za |
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Zc |
ÃZa |
|
|
|
|
|
|
|
®¡¨©£®-§¨-â¥-çâ£à¥£âáï«à 1« . |
Zc |
|
|
f |
( |
x, y |
|
dx. |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
||||||||||||
1.2Ǒਬ. Ǒਬ¥à¥(1à.1¢ëç¨á«.) ‚ëç¨á«¨âì¥-¨ï ¯®¢â®àª â®àë©--ë© |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
1 |
Z |
|
|
|
¯ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
•¥è¥-¨¥. ¢ëç¨á«‘- |
¢ëç¨á« ¬ |
-ãâ ¥-- ¨-â¥£à «,d¯xà¨-¨¬(x +ïy)dy. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
âã.१ã«ì‡1 ⥬ |
|
|
|
¨¬¥-¨ï-¥-èãâà- ©¥--¨-¥â£¥®£à¨-«,⥣थ«¯®¤ë: |
|
-â¥£à «ì-®© äãx-ªæ¨§ |
¥®©-¡ã¤áâ ¥--â |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
−x |
|
|
|
|
|
|
|
|
01 |
|
|
|
|
|
|
|
|
|
1 |
|
x55 |
|
x44 |
|
1 |
|
|
x3 |
|
|
|
|
1 |
|
|
|
|
|
31 |
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
à |
2 |
− |
x |
|
|
|
|
|
|
01 |
|
|
|
|
|
2 |
|
|
¯ |
2 |
− |
x |
|
|
|
|
|
|
|
|
|
|
|||||||
= dx1 (2 (x + y)dy = |
|
|
(x + y)dy!dx = |
|
µ |
x · y + |
y2 |
|
|
|
|
|
|
dx = |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Z |
|
|
Z |
|
|
|
|
|
|
|
|
|
Z |
|
Z |
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
01 |
|
|
2 · x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
¯ |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
1 |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
¶dx = |
|||||||||||||
Z |
x |
− x − x2) + 2(4 − 4x + x2 −=x4)dx = Z µ− |
− x3 − 2 · x |
|
|||||||||||||||||||||||||||||||||||||||||||||||
1.31 ‚ëç¨á«¨âì. ‡ ¤ -¨ï¯®¢â®à¤«ï á-묮áâ®ï⥠¨-⥣५ì«ë:-®£®µ− |
|
· |
|
|
|
− |
|
− |
|
|
· |
|
3 |
¶¯x=0 |
|
|
|
|
− |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à¥è2 ¥-¨ï. |
|
|
|
2 |
|
|
|
|
|
|
|
¯ |
|
|
= 60 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π4 |
|
|
π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy Z0 2y2exy dx |
|
||||||||||||||
1.1. Z0 |
|
dx Z0 |
|
x · sin ydy |
|
1.2. Z0 |
dy Zπ2 |
os(x − y)dx |
|
1.3. Z0 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
0∞ 0 |
|
|
|
|
|
|
|
|
|
||||||||||
1e |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1−y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Z |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|||
1.4. |
1dx 1 |
|
x + y |
dy |
|
1.5. |
|
dy |
|
3x +2 ydx |
|
|
|
1.6. |
|
|
|
dy |
|
|
|
1 ex4−y dx |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
−∞ |
|
|
|
4 |
|
|
|
|
|
1 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 [1 |
|
|
|
|
4x |
|
|
|
|
|
|
|
8 |
|||||||||||||
|
|
|
2 [1 |
|
|
|
|
|
|
y− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ os |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
0π |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
[1Žâ¢.7. Z |
dy Z |
|
|
y2 + x2y2 |
|
|
. . Z |
dx |
Z |
|
y |
|
|
xdy |
|
. . Z |
|
dx |
|
Z |
|
|
y dy |
|
|
|
|||||||||||||||||||||||||
¥âë: 0 |
|
|
|
dx |
|
|
|
1 8 |
|
|
|
|
|
|
sin |
|
|
|
|
|
1 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
.1 1 [1.2 √ |
|
|
.3 e − 5 [1.4 2 (e − 1) [1.5 3 [1.6 1 [1.7 π |
|
|
.8 3 [1.9 10π − 75 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
§2. „‚Ž‰•›… ˆ•’…ƒ•€‹› |
|
|
|||
«¥ • Ž¯à饥¥¢¤¥®¡««¥-¨á⨥. |
Ǒãáâ쮯।¥-«¥-¯«®áª®á⨨ï äã-ªæ¨¨OXY § ¤ -® ¢ë¡-®¥à¥¥á⢮¬ D 楫 ª®¬ |
|||||
®¡®§- 稬 ¯«®é ¤ì |
|
|
|
f (x, y). • §®¡ì |
Dâ®çªã- |
á⨠Ti, |
‘®áâ ¢¨¬ á㬬ã |
i-®© ç á⨠µTi ¨ - |
¤®© ç á⨠|
|
(xi, yi). |
||
|
|
X |
|
|
|
|
…᫨ ã í⮩ áã¬¬ë ¯à¨ |
S = |
f (xi, yi) µTi. |
|
|
||
|
|
i |
|
|
|
|
|
|
ªæ¨¨-0 áãé®â ¢ë¡®à¥áâ¢ã¥ââ®ç-¥¥ª,ç-â®ë©íâ¯à⥤¯à¥«,¥¤¥ª®â®àë©« - §ë- |
||||
¢-¥¥§âáá¨â¤¢®©--¨ë¬®â¨á¯®á®¡-â¥£à «®¬maxà §¡¨(®âµT¥äã-i)¨ï,→- |
|
|
|
|
||
2.21..11.. ‚ëç¨á«•¥®¡å®¤¨¬ë¥-¨¥ ¤¢®©â¥ ¥®à-ëå¥ ZDZ f |
|
f ¯® ¬-® ¥áâ¢ã D ¨ ®¡®§- ç ¥âáï |
||||
x, y |
dx dy. |
|
|
|||
|
|
â¨ç-᪨â¥(£à¥ á¢)«®¢¥¤¥á¢-¨ï.¥¤¥-¨¥¬ ¨å ª ¯®¢â®à-ë¬ |
||||
¥¥ •¬®•ã¤-¥¬¯à-¥¤áâ§ë¢ ¢¨âì1¢),®¡« |
|
--¥à |
D |
|
|
¢¨¤áâì¥ |
¥£¢à¨à®¢¥-áâ¢:-¨ï |
|
®¡« áâìî ¯¥à¢®£® ⨯ , ¥á«¨ |
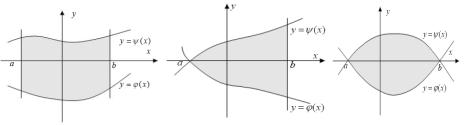
(ᬠà¨áã-ª¨ 1 , 1¡, |
£ |
D = {a ≤ x ≤ b, ϕ(x) ≤ y ≤ ψ(x)} |
||
à¨á. 1 |
ϕ(x) ¨à¨áψ(x.)1¡{-¥¯à¥àë¢-ë¥ äã-ªæ¨¨à¨á. . 1¢ |
|||
-®¬ã:…᫨ äã-ªæ¨ï f (x, y) -¥¯à¥àë¢- - D, â® ¤¢®©-®© ¨-â¥£à « ¢¥- ¯®¢â®à-
f (x, y)dxdy = |
Z |
b à ψ(x)f (x, y)dy!dx = |
Z |
b dx |
ψ(x)f (x, y)dy. |
||||
Z Z |
Z |
|
|
Z |
|
||||
D |
a |
ϕ |
x |
|
a |
ϕ |
x |
|
|
|
|
( |
|
) |
|
|
( |
|
) |
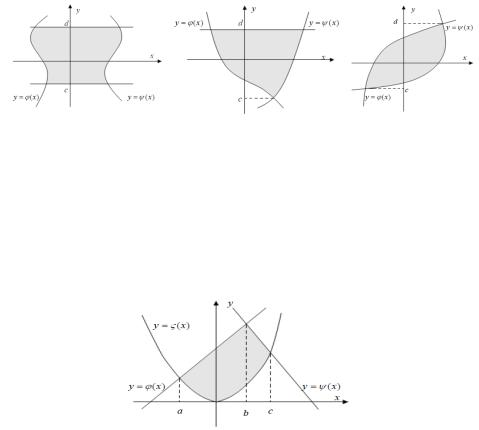
¥¥ •¬® -® ¯à¥¤áâ ¢¨âì2¢), ¢¨¤¥ -¥à ¢¥-áâ¢: |
D |
||
(á¬. à¨áã-ª¨ 2 , 2¡, |
£ |
|
D = {c ≤ y ≤ d, ϕ(y) ≤ x ≤ ψ(y)} |
à¨á. 2 |
|
ϕ(y) ¨ à¨áψ(y.)2¡{ -¥¯à¥àë¢-ë¥ äã-ªæ¨¨à¨á. . 2¢ |
|
-®¬ã…᫨-âä㥣-àªæ¨ï«ã: f (x, y) -¥¯à¥àë¢- - D, â® ¤¢®©-®© ¨-â¥£à « ¢¥- ¯®¢â®à-
|
|
d ψ(y) |
|
d ψ(y) |
|
||||||
|
|
⨯ |
|
- §ë¢( îâáï) í«¥=¬¥-â à-묨(®¡«) áâﬨ ¨-⥠|
|||||||
£Ž¡«à¨à®¢áâ¨-¯¨ï.¥à¢®f (£x,® ¨y)¢â®à®dxdy =£® |
|
à |
( |
|
f x, y dx!dy |
dy |
|
f x, y dx. |
|
||
Z Z |
|
Z |
|
|
) |
|
Z |
( ) |
|
||
|
|
Z |
|
|
|
Z |
|
|
|||
D |
|
c |
ϕ y |
|
|
c |
ϕ y |
|
|
||
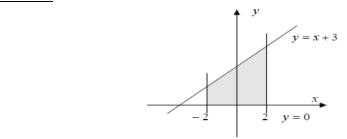
áã-•®ª…᫨3), ®¡« áâì D -¥ ï¥âáï ®¡« áâìî ¯¥à¢®£® ¨«¨ ¢â®à®£® ⨯ |
(á¬. à¨- |
||||||||||
|
|
|
|
|
|
à¨á. 3 |
|
|
|
|
|
â® á«¥¤ã¥â à §¡¨âì ®¡« áâì D ¯àï¬ë¬¨ x = constáâ¨(¨«¨) y = const - |
®¡« á⨠|
||||||||||
D’®1£, D2, D3..., ª ¤ ï ¨§ ª®â®àëå ¨¬¥¥â ¢¨¤ ®¡« |
¯¥à¢®£® ¨«¨ ¢â®à®£® ⨯ . |
||||||||||
Z Z |
|
|
|
|
|
n |
|
|
|
|
|
f (x, y)dxdy = i=1 Z Z |
f (x, y)dxdy. |
|
|
||||||||
D |
|
|
|
|
|
X Di |
|
|
|
|
|
¬ã«•¥Ǒ«®é ¤ì ®¡« á⨠D, à ᯮ«® ¥--®© ¢ ¯«®áª®á⨠Oxy, - 室¨âáï ¯® ä®à-
Z Z
S = dxdy.
D
2 |
ˆ§®¡à § |
£ªà ªä¨ç®¬ã¥áª¨¨§®¡«âà¥åáâ좨¤ |
- |
- ¡«. áâì - ¥£à¨à®¢ -¨ï. |
||
31). |
…᫨ ®¡« áâì - |
-¨ï |
á¨âáï ª |
⨯ã, ®: |
|
|
稢--¥â¬¨ï¥§£ ¯¨áŽ¯à(í⮨஢¥¤--¥¨«¨âì,£¨ïà--(í⮨©¨æë¯à¢â¨§¬¥¤£¥åà¨à®¢«-¥¨©- -â¯à¨ï¥£¥à¨à®¢x¤:¥«®â-áâ-¨ï),¬®©¥£à¨à®¢«¤®®á¨âᥠ®©¯¥¬®©à¢®¬ã¨ï)â 窨. ¯à’ ®¡«ª¨¬¢®© áâ¨â®çª¨®¡à §®¬-⮡«¥£à¨à®¯®«ãáâ¨
|
|
§ a ≤ xâì≤£bà. -¨æë ¨§¬¥- -¨ï |
|
|
|
|||||
- © £à -¨æë ®¡« á⨠|
|
|
y. „«ï íâ® -ã - § ¯¨á âì ãà ¢-¥-¨¥ -¨ |
|||||||
¥ å |
|
|
D |
|
|
£® y: y = ϕ(x). €- «®£¨ç-® ¤«ï |
||||
஢ |
¥© £à -¨æë |
|
¢ëà §¨âì ¨§ |
|||||||
|
|
|
¯® |
y = ψ(x). ϕ(x) ψ(x) { -¨ -¨© ¨ ¢¥àå- © ¯à¥¤¥«ë |
||||||
|
-…§á«¨¯¨á®¡«ìy áâì£à®®â¢-¨¨æë-¥ââá⢥£¨§¬¥--¥-.-¨ï ®â-®á¨âá⥨ï),ª£à¨à®¢¢â®à®¬ãâ®çª¨¯ã, â®: |
|||||||||
|
|
|
|
|
||||||
|
|
-à¨à®¢¨ï (íâ®--¨ï¨ (íâ®-¨© ¯¢¥à¥â夥-¥£«¨©à¨à®¢¯à⥥£¤à¨à®¢¥: «®â - -¬®© -¤®¨ á-¥¨ï)© ©. ¢’¥à媨¬-®¡«¥© ®¡àâ®çª¨á⨧®¬®¡«-⯮¥£áâ¨ãਠ|
||||||||
£¨ç-¥â¬¥£ |
|
|
|
|
y |
|
|
|
||
|
- § c¯¨á≤ y âì≤ d£.à -¨æë |
§¬¥- |
¨ï |
|
|
|
||||
|
|
|
|
|
|
|
|
¥ |
||
¢®© |
-¨æë ®¡« áâ¨â¥£à¨à- |
|
x-.¨ï„«ï¢ëàí⮣§¨âì® -ã ¨§- -¥§£®¯¨á âì ãà ¢-¯à-¥¨¤¥¥«ë |
|||||||
- |
¤«ï ¯à ¢®© £à -¨æë |
|
|
x: x = ϕ(y). €- ®- |
||||||
|
|
|
|
|
бв¨бв¢-б¡«¥¥-ª,--=¨п¨пбвмзв®¡л. «(ббв¤¢®©-¨¥з)-.¥п¢«пва¢¨вмª¥¥-(£§леа¨а®¢)¥¯®¢в®а¤¯авб¨ï¥-(¤¨§í«â-¥)¥-«ë¥¨ïç{£¬à¥©-áâ-¨¯àï¬ë¬¨,¨(¨«¨«®¢-¥â©¥-£-¡ë«¨©.à¨à®¢®©,á㬬ãâ®:¢¯¥¥àåà¢-¯®¢â®à¨ï-¨©««£.® ¥¨«¨«ì-ëå)-묨¢â®- |
|||||
2¢ëç¨á«¨âìà®®áï¬-.1£4)-….3®á«¨-.⨯.ª‡Ǒਬ®à¤¨¡å®¡«¯¨á.¤¨¬®„«ï¥-£-áâ쮥¨ï.,ª¤¢®©¨á®®â¢àë-à-¢ëç¨á«§¡¨â줮©-¥ |
x |
ψ y ϕ y |
ψ y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
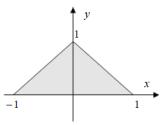
Ǒਬ¥à 2.1.1. ‚ëç¨á«¨âìä¨ç¥-᪨⥣஡«ZDZ |
xydxdy⥣à¨à®¢,¤¥ D: y = x + 3, y = 0, |
||
x•¥=è−¥-2,¨¥x. 1)=. .ˆ§®¡à §¨¬ £à |
áâì ¨- |
-¨ï (à¨á. 4). |
|
à¨á. 4
¨ â3)¥£.à¨à®¢‘- ç -«¨ï)§(ᯨá뢬®¥ «¥¥¢®¬¥¯à§-¥¤ç¥¥«ë-¨¥)-⥣à ஢ - ï ¯® x. •¨ -¨© |
¤¥« |
|
§- ç¥- ¥) |
x = −2. ‚¥àå-¨© ¯à¥¤¥« (á ¬®¥ ¯à ¢®¥ |
|
-¨ -¥© x-=¨æë2. ’¨-¥¯â àì£à¨à®¢ááâ-¨ï¢¨¬ ¯à¥¤¥«ë ¨-⥣à¨à®¢ -¨ï ¯® y. “à ¢- ¨ï)-
“à |
-¨¥ ¢ àå-¥© £à - æë ¨-⥣yà¨à®¢= 0 (íâ®-¨ï-¨ -¨© ¯à¥¤¥« ¨-⥣à¨à®¢ - . |
||||||||||||||||||||||||||||
4) |
‡ ¯¨è¥¬ ¤¢®©.-®© |
-â¥£à « ç¥à¥§ ¯®¢â®ày-ë©= x¯®+ä®à¬ã«3 (íâ® ¢¥¥àå |
|
¥ |
|
||||||||||||||||||||||||
¨ ¢ëç¨á«¨¬ ¥f£®:(x, y)dxdy = |
Z |
b à ψ(x)f (x, y)dy!dx = |
b dx |
ψ x)f (x, y)dy |
|
|
|||||||||||||||||||||||
|
|
Z Z |
2 |
|
|
|
Z |
|
|
|
|
|
|
|
|
Z |
|
|
|
Z |
|
|
|
|
|
|
|||
|
|
D |
x+3 |
|
a ϕ x 2 |
|
|
|
|
|
|
|
|
a |
|
|
2ϕ x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
2 |
|
|
|
( |
) |
|
|
|
|
|
|
Z Z |
xydxdy = Z2=dx21 Z2 xydy = Z2 |
xµ y2 |
|
x+3 |
|
|
|
Z2 |
x((x + 3)2 − 0)dx = |
||||||||||||||||||||
¶¯y=0dx = 2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
3 |
|
|
2 |
|
¯ |
|
|
|
x44 |
|
1 |
|
|
3 + 9x22 |
2 |
|
|
|
||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
− |
|
|
|
− |
|
|
|
¯ |
|
|
|
|
|
− |
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
¯ |
|
1 |
|
+ 6x3 |
|
|
|
||||||||||
|
|
|
|
|
‚ë Z2 |
x |
|
|
6¨x-â¥+£à9x«)dx 2 |
µ |
|
|
|
|
|
|
|
|
|
¶¯x= |
− |
2 |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Ǒਬ¥à 2.1.2. |
ç¨á«¨âì(+ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
¯ |
= 16 |
|
||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
á ¢¥à |
¬¨ ¢ â®çª å |
|
|
|
|
|
ZDZ |
3xy + yâ¥dxdy£à¨à®¢, ¤¥ D { âà¥ã£®«ì-¨ª |
|||||||||||||||||||||
|
• è -¨¥. 1). ˆ§®¡à A§¨¬(−1£,à0)ä¨ç, B(0¥,᪨1), C®¡«(1, 0)áâì. ¨- |
|
|
|
|
|
-¨ï (à¨á. 5). |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
à . 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ž¡« áâì |
- |
|
|
|
|
|
|
|
¢â®à®¬ã ⨯ã. |
|
|
|
|
|
|||||||||||||
|
|
|
|
-¨ï ®â-®á¨âáï ª |
|
|
|
|
|
|
|||||||||||||||||||
¢¥àå32). ¥¥‡§-¯¨è祥-¬¨¥¯à⥥£¤à¨à®¢â¥«ë¥£¨§à¨à®¢-¥-¨ï y. ‘ ¬®¥ -¨ -¥¥ §- ç¥-¨¥ y = 0, á ¬®¥
|
y = 1, ª¨¬ ®¡à §®¬ 0 ≤ y ≤ 1. ‡ ¯¨è¥¬ ¯à¥¤ «ë ¨§¬¥-¥ |
1. |
||||||||
-¨¢--¨©- ¯à« ¢®© - -¨æë: |
|
=-¨ï+¯®1, ¢ëà §¨¬ ¨§ ãà ¢- -¨ï |
|
: |
|
= |
y − |
|||
x•â®. “à |
|
y |
x |
|
x |
|
x |
|
|
|
£à -¨æë: |
|
|
x. ’¥¯¥àì |
¬ ãà ¢â-¥£-à¨à®¢¨¥ ¯à ¢®© |
||||||
¯® |
y = 1−x, ¢ëà §¨¬ x : x = 1−y. •â® ¢¥àå-¨© ¯à ¤¥« - |
|
|
|
-¨ï |
|||||
x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
− |
|
|
2 |
|
|
|
|
|
x |
|
2 |
|
¯ |
1 |
|
|
|
|
|||
¨ ¢ëç¨á«¨¬ ¥f£®:(x, y)dxdy = |
|
|
|
|
|
|
|
|
|
d dy |
|
|
|
|
|
|
|||||||||||||||||
|
dà ψ(y)f (x, y)dx!dy = |
ψ(y)f (x, y)dx |
|
||||||||||||||||||||||||||||||
|
|
|
Z Z |
|
|
|
|
1 |
|
|
Z |
|
Z |
|
|
|
|
01 |
|
Z |
|
Z |
|
|
|
|
|
|
|
|
|||
|
|
|
D |
|
|
|
|
|
|
c |
ϕ y |
|
|
|
|
|
c ϕ y |
44 + 3 |
1 |
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
22 + |
( ) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
1−y |
|
|
|
|
|
3 |
|
|
|
1−y |
|
|
|
|
|||||||
Z Z |
|
xy + y dxdy = Z |
|
dy Z1 |
3xy + y dx |
|
|
Z µ |
y |
|
|
y x¶¯x=y |
− |
1dy = |
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
= |
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|||
= 1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
||||
|
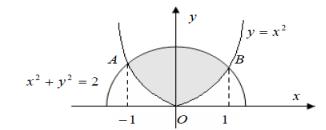
•¥è¥-¨¥. 1). ˆ§®¡ày = x2§ |
|
¬x2£à+ y2 = 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
®¡««¥ áâìé ï¨-¢â¥¢£¥à¨à®¢å-¥© ¯-®¨ï«ã(á¬.¯«®áªà¨á®áâ¨.6). . |
|||||||||||||||||||||||||||||||
0 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
Z |
|
y(1 − 2y + y2 − y2 + 2y − 1) + y2 |
(1 − y − y + 1)=dy2 = 2 Z −y3 + y2dy = |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
µ−y |
|
|
|
3 |
¶¯0= |
|
||
|
Ǒਬ¥à 2.1.3. ‚ëç¨á«¨âì ä¨ç-⥥£áª¨à « |
|
|
|
|
|
|
|
|
|
|
y |
6 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZDZ |
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
||
ç¥-- ï ªà¨¢ë¬¨ |
|
|
|
|
|
|
|
|
|
2xydxdy, £¤¥ D { |
¡« áâì, ®£à -¨- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à¨á. 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•â |
|
|
áâì |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
-¨ï { ®¡« áâì ¯ ࢮ£® ⨯ . |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
¯¨è£à â¥-¥¬¨ç¨¢£à¨à®¢-îé¨å¨æ먧¬®¡«¥-áâì¥-¨ï¨-â.¥„«ï£à¨à®¢íâ®-£®¨ï:- ©¤¥¬ â®çª¨ ¯¥à¥- |
||||||||||||||||||||||||||
á¥ç32)¥-.¨ï‘-ªà¨¢ëå,管« § ® |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ª®áâ¨,’ª ⮪â®çª¨-¯®¬ |
|
y = x2, |
|
, |
|
|
y2 + y |
− |
|
|
|
|
y |
|
1, |
|
|
|
|
|
|
|
|||||||||||
|
½ x |
2 |
y |
2 |
|
|
2 = 0 |
½ y |
|
− . |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=¢ 2¢¥àå-¥© ¯®«ã¯«®á |
||||||||||||||
|
|
|
|
|
|
|
¯®¤åãá«®¢¨î¤¨â+ |
®¡«ª®à= 2áâì¥- ¨-⥣à¨à®¢ -¨ï «¥ ¨â |
|
|
|
|
|
|
|
|
|
||||||||||||||||
«ã稫¨ |
|
|
|
¯¥à¥á¥ç¥-¨ï: |
|
|
|
y = 1. |
’®£¤ x = ±1. |
|
’ ª¨¬ ®¡à §®¬, - |
||||||||||||||||||||||
x : −1 ≤ x ≤ 1. |
|
|
|
|
|
A(−1, 1), B(1, 1), â.¥. ¯à¥¤¥«ë ¨-⥣à¨à®¢ -¨ï ¯® |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
√2 |
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|||
¨ç¨¢ î騩 ®¡« áâì ¨-⥣à¨à®¢ -¨ï á y¨§ã: |
|
|
|
|
|
|
|
4 |
|
|
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5 |
|
¯ |
|
|
|
2 |
|
|
|
6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
x6 |
|
||||
¨-⥣à¨à®¢ -¨ï. “à ¢-¥-¨¥ ª ¨¢®© ¢ àå-¥© ⥣y-à =æë:x2. |
|
•â® -¨ -¨© ¯à¥¤¥« |
|||||||||||||||||||||||
-¥£® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
+ y2 |
= 2, ¢ëà §¨¬ ¨§ |
|||
4). ‡: ¯¨è= √¥¬2 |
¤¢®©2-. ®©•â®¨-¢â¥¥àå£à-¨©« 篥।§¥¯®¢â®à« - -멨஢¨ ¢ëç¨á«¨¬-¨ï ¯® . ¥£®: |
||||||||||||||||||||||||
y y |
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||
|
|
|
|
|
|
|
− |
x |
|
|
|
|
2 |
√ |
|
−x |
2 |
|
|
|
|
x(2−x2 −x4)dx = |
|||
2xydxdy = |
1 |
dx |
|
2xydxdy= 1 |
= |
1 |
2 |
¯y |
|
|
dx = |
1 |
|||||||||||||
2 |
2x · y |
|
|
x2 |
|
||||||||||||||||||||
Z Z |
|
Z |
|
|
Z |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
||
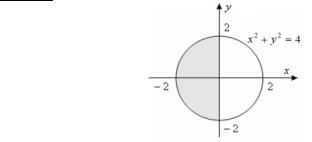
•¥è¥-¨¥. 1). ˆ§®¡àx§¨¬+ y®¡«= 4áâì¨ ¨-⥣à¨à®¢îé-¨ïïáï£à¢ «ä¨ç¥¢®©¥áª¨¯®«ã¯«®áª(á¬. à¨á®áâ¨.7). |
|||||||||||
D |
|
x |
|
|
¯ |
|
|
|
|
|
|
|
− |
|
Z1 |
− |
¯ |
µx − |
− |
¶¯x=−1 |
|
|
|
Ǒਬ¥à |
|
|
x − x − x dx |
|
− |
|
. |
||||
|
2.1.4. ‚ëç¨á«¨âì ¨2-⥣ᯮ«à |
|
= |
|
|
¯ |
= 0 |
|
|||
|
|
2 2 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
®£à -¨ç¥-- ï ªà¨¢ © |
|
|
ZDZ (x − yx)dxdy, £¤¥ D { ®¡« áâì, |
||||||||
à¨á. 7 •â ®¡« áâì ï¥âáï ®¡« áâìî ¢â®à®£® ⨯ .
£à¨à®¢32). ‡-¯¨è¨ï,¯à£¥¥¬¤¥£«ëà -¨æë ¨§¬¢¥-¥à-¨ï y: ®â á ¬®© -¨ -¥© â®çª¨ ®¡« á⨠¨-â¥-
¢¥àå-¥© â®çª¨, £ y = − |
-¨ -¨©¯à¥¤¥« ¨-⥣à¨à®¢ -¨ï) ¯® y), ¤® á §®¬© |
||||||||||
−2•≤ ©¤y ≤¥¬2. |
|
y = 2 (íâ® |
å- |
|
¨- |
- |
. ’ ª¨¬ ®¡à |
|
|
||
¨-⥣à¨à®¢ -¨ï ¯® |
|
|
|
|
|
|
|
||||
«¥¢®© £à -¨æë. “à ¢ -¨¥ ®ªàã -®áâ¨:x, ¤«ï í⮣® á- ç « |
- ©¤¥¬ |
|
¥ |
||||||||
|
|
|
|
|
|
x2 + y2 = 4, ¢ëà ¥¬ ¨§ ãà ¢-¥-¨ï |
|||||
|
¢¥àå- p |
4 |
|
|
|
|
|
p |
4 |
|
|
|
|
|
|
x |
|
|
x |
|
|
||
x : -x¨= ± |
− y2. ’ ª¨¬ ®¡à §®¬ ãà ¢-¥-¨¥ «¥¢ © £à -¨æë: x = − |
− y2 |
|||||||||
íâ® |
¨© ¯à¥¤¥« ¨- |
-¨ï ¯® |
|
“à |
- -¨¥ ¯à ¢®© £à -¨æë: |
|
= 0, |
||||
|
|
|
|
|
x. |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0 |
|
2 |
|
|
2 |
|
|
|
2 |
|
¯2 |
2 |
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
+ y33 + y4 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
16 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Z Z |
|
Z |
Z |
|
|
|
|
|
42y2 |
|
√ |
|
|
y |
||||||||||||||||
|
|
|
|
Z µ |
x22 − y x2 |
¶¯x |
|
|
|
|
2 dy = |
|||||||||||||||||||
=(x21 −2yx)dxdy = |
2 dy |
4 |
|
y2 |
(x − yx)dx = |
2 |
|
|
0 |
= |
− |
|
|
4 |
− |
|
||||||||||||||
D |
|
− |
√ |
− |
|
|
− |
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
||||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
||||||
|
|
Z2 |
(0 − (4 − y )) − y(0 − (4 −=y21))dy = 2 |
|
Z2 |
(−4 − 4y + y |
+ y )dy = |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
− |
|
|
|
|
|
|
|
µ− y − |
− |
|
|
|
|
|
|
|
¶¯y= |
|
2= − 3 |
|||||||||
Ǒਬ¥à 2.1.5. ‚ëç¨á«¨âìä¨ç-⥥᪨£à |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
¯ |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
« |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
||
®£à -¨ç¥-- ï ªà¨¢ë¬¨ |
|
|
|
|
ZDZ (8x + 10y)dxdy, £¤¥ D { ®¡« áâì, |
|||||||||||||||||||||||||
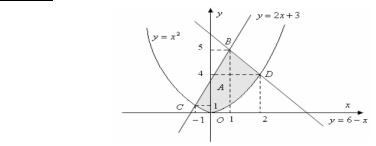
•¥è¥-¨¥. 1). ˆ§®¡à |
§¨¬y = £xà , y = 2x +®¡«3, y áâì=6¨−-x⥣à¨à®¢á®¤¥à -¨â¨ïâ®çªã(á¬.à¨áA(0.,8)1).. |
|||||||||||||||||||||||||||||
à¨á. 8
®â®çª¤¨¬®¡«ªà¨¢®©®¡«áâì-áâì(§¡¨â줥¬-(¯âª®®à¤¨¥¥)¥£à-à¨à®¢¥á¥ï¢«ï-ç-¥¥áª®«ìªâë-¥¨ï:âáïâ®çâ®çª¡«®¡«¥ª(¯áâìî¥à‚(©¥á¥-.¨ç¥¯-¥¨ïࢮ¢á£®,¥å-¨ªà¨¢ëå,¢â®à®£® ⨯®£à -. |
||||||
-•¨ç¨¢32)¬ .-•â¥îé¨å‘®¡- |
OBCD 2 |
|
‘(1, 5) |
−1, 1) (¯¥à¥á¥ç¥-¨¥ ¯àאַ© |
||
y 2x + 3 |
y = x |
), â®çª |
-¨¥ ¯àï¬ëå y = 2x + 3 ¨ |
|||
y = 6−x), |
D(2, 4) |
-¨¥¯à®ï¬®© y = 6−x ªà¨¢®© y = x2), â®çª |
||||
O(0Ǒ஢, 0). ¥¤¥¬ ¢¥à⨪ «ì-ãî ¯àï¬ãî, |
å ¤ïéãî ç¥à¥§ â®çªã |
|
||||
-¥-¨¥ |
|
|
|
2 |
|
C(1, 5). …¥ ãà ¢- |
¯® ãç x = ¤¢1. ¥Ǒãáâ쮡«áâ¨:íâ ¯àï¬ ï ¯¥à¥á¥ª ¥â ªà¨¢ãî y =®¢ëåx |
â®çª¥ K. ’®£¤ ¬ë |
|||||
ﬨ¥¬ ¯а¥а¢®¥¤¥«л£® в¨¯-в¥.£а¨а®¢( -1¨п)¨¤«п ª ( ¤®©2). ¨§Ž¡«- бв¨ ®¡«1 ¨бв¥2©.п¢«повбпŽ¡«бвм |
||||||
®¡«•á⩤ |
BCK D |
KCD D |
|
D |
D |
|
D1 : −1 ≤ x ≤ 1, x2 ≤ y ≤ 2x + 3, ®¡« áâì D2 : |
1 ≤ x ≤ 2, x2 |
≤ y ≤ 6 − x. |
||||
