diskretka

ПРОГРАММА КУРСА «ДИСКРЕТНАЯ МАТЕМАТИКА»

Теория множеств. Основные понятия

элементы

Под множеством S будем понимать любое собрание определенных и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются

элементами множества S.

Под множеством понимают объединение в единое целое определенных вполне различаемых предметов (объектов), которые при этом называются элементами образуемого ими множества.

подмн-ва

Мн-во А, каждый элемент которого является элементом другого мн-ва М, называется подмножеством данного мн-ва М.

Булеан

Булеан — множество всех подмножеств данного множества, обозначается 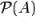или 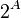(так как соответствует множеству отображений из 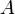в ).

Мощность

Мощность конечного множества А - это число его элементов. Мощность множества обозначают |A|.

Упорядоченное

в котором для любых двух элементов и 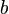имеет место или .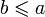

Разбиения

это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств

Множество из трех элементов 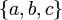может быть разбито пятью способами:

, , , ,

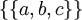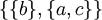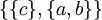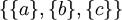
способы задания

перечислением элементов: М={a1, a2, …, ak}, т. е. списком своих элементов;

характеристическим предикатом: М={x | P(x)}(описанием характеристических свойств, которыми должны обладать его элементы);

порождающей процедурой: M={ x | x=f}, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами множества являются все объекты, которые могут быть по-

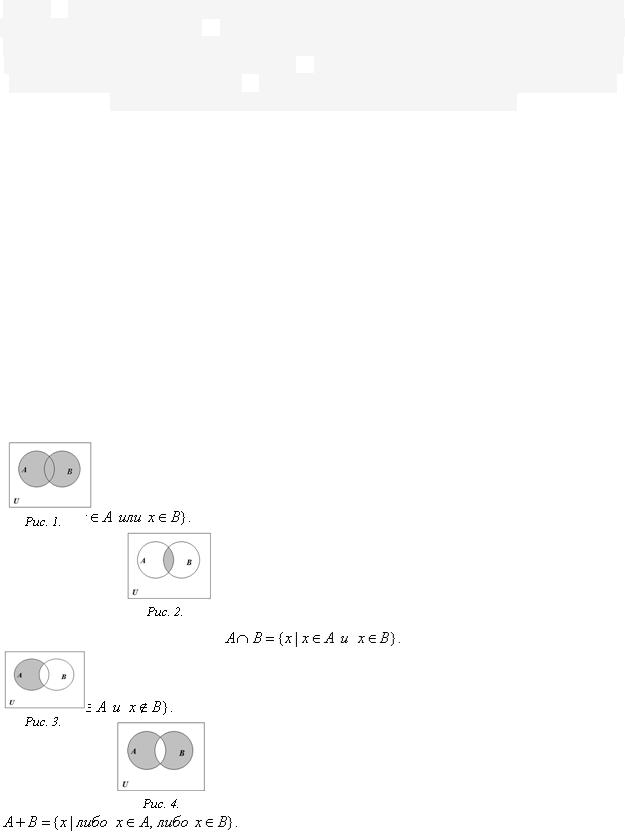
строены с помощью такой процедуры. Например, множество всех целых чисел, являющихся степенями двойки.

Парадоксы теории множеств.

Пусть — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли само себя в качестве элемента? Если предположить, что содержит, то мы получаем противоречие с "не содержат себя в качестве своего элемента". Если предположить, что не содержит себя, как элемент, то вновь возникает противоречие, ведь — множество всех множеств, а значит, должно содержать все возможные элементы, включая и себя.

основные операции над множествами.

Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А

(рис. 5):

Пример 5. С помощью диаграмм Эйлера – Венна проиллюстрируем справедливость соотношения 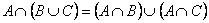(рис. 6).

3) фундаментальные алгебры. алгебра Кантора.

4) Отношения, бинарные отношения. Отношение эквивалентности.

пределение. Упорядоченная пара <x, y> интуитивно определяется как совокупность, состоящая из двух элементов х и у, расположенных в определенном порядке. Две пары <x,y>, <u, v> считаются равными тогда и только тогда, ко-

гда x=u, y=v.

Упорядоченная n-ка элементов х1, …, хn обозначается <x1, …, xn>. Определение. Прямым произведением множеств X и Y называется множество 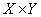, элементами которого являются все возможные упорядоченные пары <x, y>, такие, что .

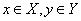Определение. Прямым произведением множеств Х1, Х2, …, Хn называется совокупность всех упорядоченных n-ок <x1, …, xn> таких, что 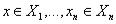. Если

Х1=Х2=…Хn, то пишут 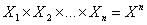. Пример 7.

Пусть X={1, 2, 3}, Y={0, 1}. Тогда

; .

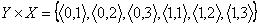Пусть Х – множество точек отрезка [0, 1], а Y – множество точек отрезка [1, 2]. Тогда - множество точек квадрата с вершинами в точках (0, 1), (0,

2), (1, 1), (1,2).

Определение. Бинарным (или двуместным) отношением r называется множество упорядоченных пар.

Если r есть отношение и пара <x, y> принадлежит этому отношению, то наряду с записью <x, y>Оr употребляется запись xry. Элементы х и у называются координатами (или компонентами) отношения r.

Определение. Отношение r на множестве Х называется рефлексивным, если для любого элемента хОХ выполняется хr х.

Определение. Отношение r на множестве Х называется симметричным, если для любых х, уОХ из хr у следует уr х.

Определение. Отношение r на множестве Х называется транзитивным, если для любых х, у, zОХ из хr у и уr z следует хr z.

Определение. Рефлексивное, симметричное, транзитивное отношение на множестве Х называется отношением эквивалентности на множестве Х.

Пример 11.

Отношение равенства на множестве целых чисел есть отношение эквивалентности.

Отношение подобия на множестве треугольников есть отношение эквивалентности.

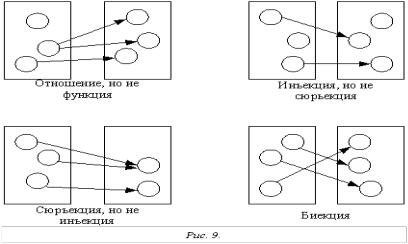
Рисунок 9 иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.

Определение. Гомоморфизм, который является биекцией, называет-

ся изоморфизмом.

Это отображение алгебраической системы А, сохраняющее основные операции и основные соотношения.

Отображение 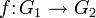называется гомоморфизмом групп , , 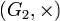если оно одну групповую операцию переводит в другую: .

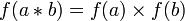6) упорядоченные множества и решетки. Основные понятия.

7) принцип математической индукции.

Пусть A(n) — некоторое утверждение, зависящее от натурального параметра n и имеющее смысл для всех натуральных чисел n. Если A(1) выполняется (база индукции) и для любого натурального числа n из того, что A(n) выполняется, следует, что A(n+1) выполняется (шаг индукции), то A(m) справедливо для всех натуральных чисел m.

8) особенности бесконечных множеств. Основные понятия. Счетность. Кардинальная эквивалентность. кардинальные числа.

Бесконечное множество — множество, не являющееся конечным. Можно дать ещё несколько эквивалентных определений бесконечного множества:

Множество, в котором для любого натурального числа найдётся конечное подмножество из элементов.

Множество, в котором найдётся счётное подмножество.

Яблонский

1) сущ-ет функция fi принадлежащая S, не сохр. константу 0; 2)сущ-ет ф-ия fi принадл. S, не сохр. конст.1; 3)сущ-ет хотя бы 1 нелинейная ф-ия 4) сущ-ет несамодвойственная ф-ия 5) сущ-ет немонотонная ф-ия в S

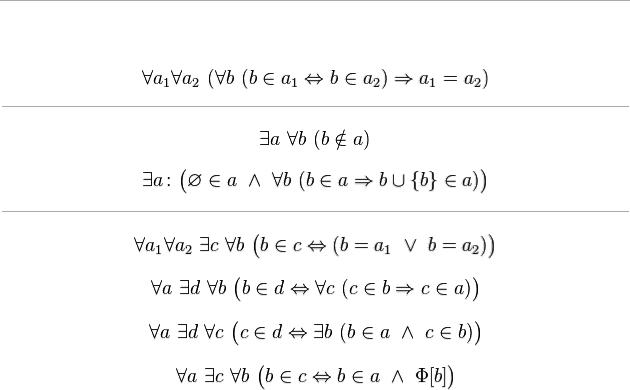
Множество, для которого существует биекция с некоторым его собственным подмножеством.

Всякое бесконечное множество M равномощно некоторому собственному подмножеству. Всякое бесконечное множество содержит счетное подмножество.

Втеории множеств, сч тное множество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Более формаль-

но: множество является счётным, если существует биекция 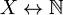, где обозначает множество всех натуральных чисел. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.

Любое подмножество счётного множества не более чем счётно (т.е. конечно или счётно).[1]

Объединение конечного или счётного числа счётных множеств счётно.[1]

Прямое произведение конечного числа счётных множеств счётно.

Множество всех конечных подмножеств счётного множества счётно.

Множество всех подмножеств счётного множества континуально и, в частности, не является счётным.

9) система аксиом Цермело-Френкеля (ZF). Система аксиом теории множеств (ZFC).

Аксиомы ZFC

Аксиомами ZFC называется следующая совокупность высказываний теории множеств: