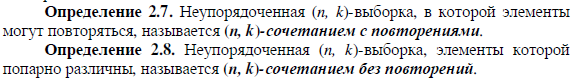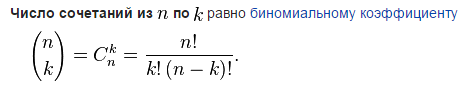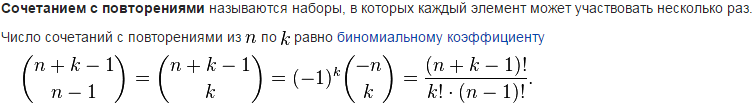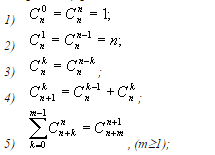1.Множества

1) Множество — это набор, совокупность каких-либо вполне различаемых объектов, называемых его элементами, обладающими общими для всех их и только их свойствами, и рассматриваемых как единое целое. Каждое множество состоит из того или иного набора объектов, которые называются элементами множества. Множества принято обозначать прописными буквами латинского алфавита: A,B,C,… Множество, не содержащее ни одного элемента, называется пустым множеством. Элементами мн-ва могут быть множества. Мн-ва, элементами которого являются другие множества, называется семейством(классом).

3)Множество может задаваться:1)путем перечисления его элементов.(A={a,b,c,d} Обычно перечислением задают конечные множества.2) характеристическим свойством(св-во, которым обладает каждый элемент(A={x|p(x)}.3) Порождающей процедурой(способ получения элементов нового мн-ва из уже полученных эл-ов или из других объектов.

4) Число элементов конечного множества называется его мощностью.

5) Множество Х является подмножеством Y, если любой элемент множества Х принадлежит множеству Y. Это еще называется нестрогим включением.

6)Включения и равенство

Когда хотят подчеркнуть, что в множестве У есть обязательно элементы, отличные от элементов множества Х, то пишут ХУ. Это называетсястрогим включением. если любой элемент множества Х принадлежит множеству Y называется нестрогим включением.Два множества называются равными (X = Y), если между их элементами можно установить взаимно-однозначное соответствие.Множество X содержится во множестве Y (множество Y включает множество X), если каждый элемент X принадлежит Y:

7)Булеан

8)

9)

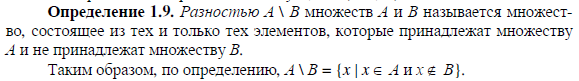
10)

11)Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией (*) и двумя выделенными элементами называется булевой алгеброй, если выполнены свойства (аксиомы булевой алгебры).Булева алгебра всех подмножеств данного множества.

U = {a1, a2… an)

[U] = N

[P(U)] = 2n

Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.

Объединение эквивалентно V, пересечение - &, дополнение - *, пустое множество – 0, а универсальное – I. Все аксиомы булевой алгебры справедливы в операциях над множествами.

12)Если число элементов множества неограниченно, то такое множество называется бесконечным. Любое бесконечное множество имеет счетное подмножество.

13)Множества, между которыми можно установить взаимно-однозначное соответствие, называются равномощными (имеющими одинаковую мощность, эквивалентными). Равномощность множеств обозначается символом "~": А ~ В. Для бесконечных множеств мощность множества может совпадать с мощностью его собственного подмножества. Мощность бесконечного мн-ва не изменится если его объединить с конечным ли счетным мн-вом. Во всяком бесконечном мн-ве есть собственное подмн-во, равномощное самому мн-ву. Мн-во всеех подмн-в всякого счетного мн-ва есть мн-во мощности континуума.

14) все элементы счётного множества можно перенумеровать, то есть обозначить натуральными числами. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел. Св-ва счетных множеств: 1) объединение конечного и счетного множеств счетно, 2)объединение двух счетных мн-в счетно, 3) декартово произведение 2 счетных мн-в счетно

15) Конти́нуумв теории множеств — мощность множества всех вещественных чисел. Обозначается строчной латинской буквойcво фрактурном начертании:C. Множество, имеющее мощность континуум, называется континуа́льным множеством.

16)Иерархия бесконечных мн-в

|B(A)=2^N Класс счетных мн-в

|B(N)|=2^w Класс мн-в мощности континуума

|B(B(N)))|=2^2w Класс мн-в мощности континуума 2-го порядка

|B(B(B(N)))|=2^2*2w Класс мн-в мощности 3-го порядка

17)Гипотеза КантораЛюбое бесконечное подмножество континуума является либо счётным, либо континуальным. Другими словами, мощность континуума — наименьшая, превосходящая мощность счетного множества, и «промежуточных» мощностей между счетным множеством и континуумом нет. Мощность беконечных множеств образуют дискретный ряд

2.Комбинаторика

1)Комбинаторика – раздел дискретной математики, который посвящен решению задач пересчёта и перечисления элементов множества, обладающих заданным набором свойств.

Если требуется найти число элементов, принадлежащих данному множеству и обладающих заданными свойствами, то это задача пересчета. Если необходимо выделить все элементы мн-ва. Удовлетворяющие заданным св-ам, то это задача перечисления.

2)Если из множества предметов выбирается некоторое подмножество, то его называют выборкой. Выборки бывают упорядоченные и неупорядоченные. Выборкой объема  из множества  называется всякая последовательность из  элементов множества .

3) Расположение элементов  выборки в определенном порядке называется - упорядочением , при этом выборка называется упорядоченной, в противном случае – неупорядоченной.

4) Правило произведения: пусть имеется n множеств A₁, A₂, …, A_n содержащих m₁, m₂, …, m_n элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а₁, а₂, ..., а_n), где а_i Î А _i1 (i = 1, 2, …, n), равно m₁ · m₂ · … · m_n.

5) Теорема «Мощность декартова произведения конечных множеств»

Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.

| А₁|=m₁…| А_n |=m_n

| А₁×…×А_n |= m₁*...*m_n

1)n=1

| А₁|=m₁

2) Пусть теорема верна при n=k

Докажем для n=k+1

| А₁×…×А_k |= m₁*...*m_k

| А₁×…×А_k+1 |= (m₁*...*m_k )m_k+1

6) Правило суммы: пусть имеется n попарно непересекающихся множеств A₁, A₂, …, A_n , содержащих m₁, m₂, …, m_nэлементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m₁ + m₂ + … + m_n.

7)Мощность объединения множеств.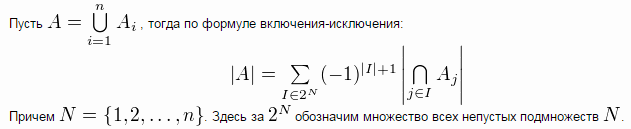

8)Размещения с повторениями и без

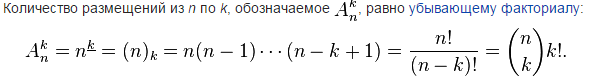
9)Перестановки

Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.

10)Сочетания и их св-ва