Diskret

1.Множества

1) Множество — это набор, совокупность каких-либо вполне различаемых объектов, называемых его элементами, обладающими общими для всех их и только их свойствами, и

рассматриваемых как единое целое. Каждое множество состоит из того или иного набора объектов, которые называются элементами множества. Множества принято обозначать прописными буквами латинского алфавита: A,B,C,…Множество, не содержащее ни одного элемента, называется пустым множеством. Элементами мн-ва могут быть множества. Мн-ва, элементами которого являются другие множества, называется семейством(классом). 3)Множество может задаваться:1)путем перечисления его элементов.(A={a,b,c,d} Обычно перечислением задают конечные множества.2) характеристическим свойством(св-во, которым обладает каждый элемент(A={x|p(x)}.3) Порождающей процедурой(способ получения элементов нового мн-ва из уже полученных эл-ов или из других объектов.

4)Число элементов конечного множества называется его мощностью.

5)Множество Х является подмножеством Y, если любой элемент множества Х принадлежит множеству Y. Это еще называется нестрогим включением.

6)Включения и равенство

Когда хотят подчеркнуть, что в множестве У есть обязательно элементы, отличные от элементов множества Х, то пишут ХУ. Это называется строгим включением.если любой элемент множества Х принадлежит множеству Y называется нестрогим включением.Два множества называются равными (X = Y), если между их элементами можно установить взаимно-однозначное соответствие.Множество X содержится во множестве Y (множество Y включает множество X), если каждый элемент X принадлежит Y:

7)Булеан

8)

9)

10)

11)Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией

(*) и двумя выделенными элементами называется булевой алгеброй, если выполнены свойства (аксиомы булевой алгебры).Булева алгебра всех подмножеств данного множества.

U = {a1, a2… an)

[U] = N [P(U)] = 2n

Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.

Объединение эквивалентно V, пересечение - &, дополнение - *, пустое множество – 0, а универсальное – I. Все аксиомы булевой алгебры справедливы в операциях над множествами.

12)Если число элементов множества неограниченно, то такое множество называется бесконечным.Любое бесконечное множество имеет счетное подмножество. 13)Множества, между которыми можно установить взаимно-однозначное соответствие, называются равномощными (имеющими одинаковую мощность, эквивалентными). Равномощность множеств обозначается символом "~": А ~ В. Для бесконечных множеств мощность множества может совпадать с мощностью его собственного подмножества.

Мощность бесконечного мн-ва не изменится если его объединить с конечным ли счетным мн-

вом. Во всяком бесконечном мн-ве есть собственное подмн-во, равномощное самому мн-ву. Мн-во всеехподмн-в всякого счетного мн-ва есть мн-во мощности континуума.

14) все элементы счётного множества можно перенумеровать, то есть обозначить натуральными числами. Другими словами, счётное множество — это множество, равномощное множеству натуральных чисел.Св-ва счетных множеств: 1) объединение

конечного и счетного множеств счетно, 2)объединение двух счетных мн-в счетно, 3) декартово произведение 2 счетных мн-в счетно

15)Конти́нуум в теории множеств — мощность множества всех вещественных чисел. Обозначается строчной латинской буквой c во фрактурном начертании: C. Множество, имеющее мощность континуум, называется континуа́льным множеством.

16)Иерархия бесконечныхмн-в

|B(A)=2NКласс счетныхмн-в |B(N)|=2wКласс мн-в мощности континуума

|B(B(N)))|=22w Класс мн-в мощности континуума 2-го порядка |B(B(B(N)))|=22*2w Класс мн-в мощности 3-го порядка

17)Гипотеза КантораЛюбое бесконечное подмножество континуума является либо счѐтным, либо континуальным. Другими словами, мощность континуума — наименьшая, превосходящая мощность счетного множества, и «промежуточных» мощностей между счетным множеством и континуумом нет. Мощность беконечных множеств образуют дискретный ряд

2.Комбинаторика

1)Комбинаторика – раздел дискретной математики, который посвящен решению задач пересчѐта и перечисления элементов множества, обладающих заданным набором свойств. Если требуется найти число элементов, принадлежащих данному множеству и обладающих заданными свойствами, то это задача пересчета. Если необходимо выделить все элементы мн-ва. Удовлетворяющие заданным св-ам, то это задача перечисления.

2)Если из множества предметов выбирается некоторое подмножество, то его называют

выборкой. Выборки бывают упорядоченные и неупорядоченные.Выборкой объема 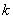из

множества называется всякая последовательность из элементов множества .

3) Расположение элементов выборки в определенном порядке называется - упорядочением , при этом выборка называется упорядоченной, в противном случае –

неупорядоченной.

4)Правило произведения: пусть имеется n множеств A1, A2, …, An содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать по одному

элементу из каждого множества, т. е. построить кортеж (а1, а2, ..., аn), где аi Î А i1 (i = 1, 2, …, n), равно m1 · m2 · … · mn.

5)Теорема «Мощность декартова произведения конечных множеств»

Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.

| А1|=m1…| Аn |=mn

| А1×…×Аn |= m1*...*mn

1)n=1

| А1|=m1

2) Пусть теорема верна при n=k Докажем для n=k+1

| А1×…×Аk |= m1*...*mk

| А1×…×Аk+1 |= (m1*...*mk )mk+1

6)Правило суммы: пусть имеется n попарно непересекающихся множеств A1, A2, …, An , содержащих m1, m2, …, mnэлементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m1 + m2 + … + mn.

7)Мощность объединения множеств.

8)Размещения с повторениями и без

9)Перестановки

Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения

элементов.

10)Сочетания и их св-ва

3. Отображение и функции

1)Определение. Соответствие, при котором каждому из элементов множества Xсопоставляется единственный элемент из множества Y,

называется отображением.

3) Если элементу x соответствует y, то y называется образом элемента x, а x -прообразом элемента y. Пишут: 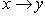или y = f(x). Множество A всех элементов 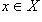, имеющих один и

тот же образ , называется полным прообразом элемента y.

4)Область определения функции — это все значения x, при которых существует функция.Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.

5)Способы задания, виды и св-ва отображений

Способы задания ВЫРАЖЕНИЕ или ФОРМУЛА. Переменная, вместо которой надо подставлять элемент из

области определения, называется аргументом функции. При этом явно указывается процедура вычисления значения f(x) функции f на аргументе x, точнее, при любом значении аргумента.

Фактически этим способом мы указываем правило вычисления значения функции f при произвольном значении аргумента x.

ТАБЛИЦА. Таблица значений функции состоит, как правило, из двух строк. В первой строке перечисляются все (!) элементы области определения, а во второй строке — соответствующие им значения функции.

ГРАФИК. Графиком функции f называется множество точек плоскости с координатами x, f(x) .

АЛГОРИТМ.X→|A|→y=y(x)

6)Операции над отображениями

Композиция y1*y2 отображение y1:a->c,такая что y(x)=y1*y2(x)=Z(ЕyϵB)(y1=y1(x)&y2(y)=Z)

7)Ф-ии как спец класс отображений

8)Классификация ф-ий по типу мн-в

3.Бинарные отношения

1)отношение

2)Бинарным отношением называется двухместное отношение между любыми двумя множествами A и B , т.е. всякое подмножество декартова произведения этих множеств: A B .

3)примерыПримеры бинарных отношений:

на множестве целых чисел отношения «делится», «делит», «равно», «больше», «меньше», «взаимно просты»;

на множестве прямых пространства отношения «параллельны», «взаимно перпендикулярны», «скрещиваются», «пересекаются», «совпадают»;

на множестве окружностей плоскости «пересекаются», «касаются», «концентричны».

4)способы задания

5) св-ва бинарных отношений

6)Проекция элемента (a, b) множества Ах В на множество А есть элемент а. Аналогично, элемент b является проекцией элемента (a, b) множества Ах В на множество В. Проекцией

множества Е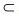 Ах В на А называется множество всех тех элементов из А, которые являются проекциями элементов из Е на множество А 7)Срез бинарного отношения. Различают срез бинарного отношения через элемент и через подмножество первого базисного множества.

8)факториалы

9)отношение эквивалентности

10) связь с разбиениями

11) Бинарное отношениеť на мн-веA(ť AxA) наз-ся отношением толерантности, если оно рефлексивно и симметрично.

12) его связь с покрытием

13) отношение порядка

14) стр-ра упорядоченных мн-в

15) Решётка— частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.Решѐтка может быть также определена как универсальная алгебра с двумя бинарными операциями (они обозначаются \/и /\ или + и ∙)

5.Булевы ф-ии

1) функции одной, 2 –х

2)св-ва булевых операций

1)A&A = A, A A = A –идемпотентность.

2)A&B = B&A, A B = B A–коммуттативность

3)A&(B&C) = (A&B)&C, A (B C) = (A B) C–ассоциотивность

4)A&(A B) = A, A A&B = A –поглошение.

5)A&(B C) = A&B A&C, A B&C = (A B)&(A C) —дистрибутивность

6)¬¬A = A – инволюция

7)Свойство констант: A&1 = A, A&0 = 0, A 1 = 1, A 0 = A

8)Закон исключения третьего и закон противоречия A ¬A = 1, A&¬A = 0

9)Правило де Моргана ¬(A&B) = ¬A ¬B, ¬(A B) = ¬A&¬B

Иногда к ним добавляют связь импликации и дизъюнкции

10) A→B = ¬A B

3) ф-ииn-переменныхОпределение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

4)Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 22n.

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2n, где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих

от n переменных) равно 2m=22n.

5)задание ф-й формуламиТак же, как составные высказывания строятся из более простых, с помощью логических операций, можно комбинировать булевы переменные с помощью булевых операций, получая булевы выражения, которые называютсяформулами.

Всякой формуле однозначно соответствует некоторая функция, при этом говорят, чтоформула реализует функцию.

6)суперпозиция

7)СДНФ СКНФ

8)представление полиномом жегалкина

9)методы нахождения полиномов

10)функц полнота

11)полная с-ма операций

В алгебре множеств 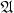для каждого определено дополнение , где 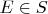- единица алгебры .

Таким образом, в кольце множеств полной системой операций может быть, например, пара операций и , а в алгебре множеств нужно ещѐ добавить нульарную операцию 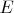(единичный элемент).