
diskretka
.pdf
Комбинаторная математика.
Основные понятия
Комбинаторика Комбинаторный анализ — раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов (безразлично, какой природы; это могут быть буквы, цифры, какие-либо предметы и т.п.).
комбинаторная конфигурация
Теория конфигураций рассматривает задачи выбора и расположения элементов некоторого, обычно конечного, множества, в соответствии с заданными правилами.
Элементарными комбинаторными конфигурациями являются сочетания, размеще-
ния, перестановки. Для подсчёта числа этих конфигураций используются правила сум-
мы и произведения.
комбинаторные объекты
Элементы из которым составляются комбинации
комбинаторные числа |
Комбинаторные числа определяют |
|
|
биноминальные коэфиценты??? |
кол-во комбинаторных объектов, |
выбранных из заданного мн-ва. |
2) размещения и сочетания постановка задач выбора и расположения.
Пусть у нас есть множество из трех элементов  . Какими способами мы можем выбрать из этих элементов два?
. Какими способами мы можем выбрать из этих элементов два?  .
.
Определение. Размещениями множества из  различных элементов по
различных элементов по  элементов
элементов  называются комбинации, которые составлены из данных
называются комбинации, которые составлены из данных  элементов по
элементов по  элементов и отличаются либо самими элемен-
элементов и отличаются либо самими элемен-
тами, либо порядком элементов.

Число всех размещений множества из  элементов по
элементов по  элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где
элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где  и
и  .
.
Теорема. Число размещений множества из  элементов по
элементов по  элементов равно
элементов равно
Определение. Сочетаниями из  различных элементов по
различных элементов по  элементов называются комбинации, которые составлены из данных
элементов называются комбинации, которые составлены из данных  элементов по
элементов по  элементов и отличаются хотя бы одним элементом (иначе говоря,
элементов и отличаются хотя бы одним элементом (иначе говоря,  - элементные подмножества данного множества из
- элементные подмножества данного множества из  элементов).
элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из  элементов по
элементов по  элементов в каждом обозначается
элементов в каждом обозначается  (от начальной буквы французского слова
(от начальной буквы французского слова
“combinasion”, что значит “сочетание”).
Числа 
Все сочетания из множества  по два —
по два —
 .
.
.
Свойства чисел 
1.  .
.
Действительно, каждому  -элементному подмножеству данного
-элементному подмножеству данного  элементного множества соответствует одно и только одно
элементного множества соответствует одно и только одно  -элементное подмножество того же множества.
-элементное подмножество того же множества.
2. 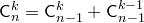 .
.
Действительно, мы можем выбирать подмножества из  элементов следующим образом: фиксируем один элемент; число
элементов следующим образом: фиксируем один элемент; число  -элементных под-
-элементных под-

множеств, содержащих этот элемент, равно ; число
; число  -элементных подмножеств, не содержащих этот элемент, равно
-элементных подмножеств, не содержащих этот элемент, равно 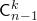 .
.
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
3) размещения, размещения с повторениями.
По правилу умножения количество размещений с повторениями из n по k, обозначаемое  , равно:[5][1][4]
, равно:[5][1][4]
Например, количество вариантов 3-значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:
4) сочетания, сочетания с повторениями. Биномиальные и полиномиальные коэффициенты.
биномиальные коэффициенты — это коэффициенты в разложении бинома
Ньютона  по степеням x. Коэффициент при
по степеням x. Коэффициент при  обозначается
обозначается  или
или  и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
и читается «биномиальный коэффициент из n по k» (или «це из n по k»):
Число сочетаний с повторениями из  по
по  равно биномиальному коэффициенту
равно биномиальному коэффициенту

Значение мультиномиального коэффициента  определено для всех целых неотрицательных чисел n и
определено для всех целых неотрицательных чисел n и  таких,
таких,
что  :
:
Биномиальный коэффициент  для неотрицательных целых чисел n, k является частным случаем мультиномиального коэффициента (для m = 2), а именно
для неотрицательных целых чисел n, k является частным случаем мультиномиального коэффициента (для m = 2), а именно
Математическая логика.
Логика высказываний.
Основные понятия пропозициональные переменные
пропозициональная переменная — переменная, значением которой может быть логическое высказывание, и (пропозициональная) формула, определяе-
мой индуктивноследующим образом[2]:
Если P — пропозициональная переменная, то P — формула.
Если A — формула, то  — формула.
— формула.
Если A и B — формулы, то  ,
,  и
и  — формулы.
— формулы.
Других формул нет.
Алфавитом называется любое непустое множество. Элементы этого множества называются символами данного алфавита. Словом в данном алфавите называется произвольная конечная последовательность символов (возможно пустая). Алфавит логики высказываний содержит следующие символы:
высказывательные переменные; логические символы;
символы скобок.
Определение. Слово в алфавите логики высказываний называется формулой, если оно удовлетворяет следующему определению:
Если P — пропозициональная переменная, то P — формула.
Если A — формула, то  — формула.
— формула.
Если A и B — формулы, то  ,
,  и
и  — формулы.
— формулы.
Других формул нет.
Логические связки и кванторы.
Конъюнкция (логическое И) & Дизъюнкция (логическое ИЛИ) Отрицание (логическое НЕ) ¬ Импликация (логическое ЕСЛИ-ТО) →. Квантор всеобщности («для каждого») Квантор существования («хотя бы один»)
интерпретация формул
Интерпретацией в узком смысле (или просто интерпретацией) называется функция
A {0,1}
такая, что (0)=0, (1)=1.
Выполнимость Противоречивость Противоречивая формула (невыполнимая, тождественно ложная) —
ложная в любой интерпретации (всегда ложная, при любых наборах значений).
Выполнимая формула (непротиворечивая, опровержимая) — не являющаяся противоречивой (не всегда ложная, не всегда истинная).
общезначимость Общезначимая формула (тавтология, тождественно истинная) — истин-
ная в любой интерпретации (всегда истинная, при любых наборах значений). Обозначается |=а. Пример: формула при любых
при любых
значениях  и
и  .
.
Равносильность Равносильность формул. Формулы 
и  равносильны, если при любых значениях входящих в них пропозициональных переменных логические значения,
равносильны, если при любых значениях входящих в них пропозициональных переменных логические значения,
получающиеся из формул  и
и  , совпадают. Обозначается:
, совпадают. Обозначается: 
( ).
).
Эквивалентные преобразования
.
простые логические функции. Тавтологии.

а) закон исключенного третьего;
б) закон отрицания противоречия; в) аконз двойного отрицания;
г) закон тождества;
|
|
|
|
д) закон контрапозиции |
; |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
е) закон силлогизма (правило це-пного закл |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
ния) |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ж) закон противоположности |
|
|
|
; |
|
|
|
|
||||||||||||||||||
з) правило добавления антецедента ("истинад- |
из |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
но") |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и) правило "из ложного что угодно" |
; |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
к) правило |
"модус (латпоненс".modus |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ponens) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л) правило "модус толленс"modus |
|
(лат. |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
tollens) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
м) правило перестановкипосы- |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
лок |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
н) правилообъединения (и разъединения)ы- |
пос |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
лок |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
о) правило разбораслуч |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ев |
|
|
|
; |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
п) правило приведения- к абсу |
|
|
|||||||||||||||||
|
ду |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||
Булевы функции
Булевой функцией f(x1, x2, …, xn) называется n-местная функция, аргументы которой принимают значения во множестве {0, 1} и сама функция принимает значения в этом же множестве.
Всякую булеву функцию от nпеременных можно задать таблицей из 2n строк, в которой в каждой строке записывают одну из оценок списка переменных, принимающих значение 0 или 1.
Основные понятия остаточная, единичная, нулевая,
ульарные функции [править]
При n = 0 количество булевых функций сводится к двум 220 = 21 = 2, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами — тождественный нуль и тождественная единица.
Таблица значений и названий нульарных булевых функций:
|
|
Значение |
|
Обозначение |
|
Название |
|
|
|
|
|||
|
0 |
|
F0,0 = 0 |
|
тождественный ноль |
|
|
1 |
|
F0,1 = 1 |
|
тождественная единица, тавтология |
|
|
|
|
|
|
|
|

Унарные функции [править]
При n = 1 число булевых функций равно 221 = 22 = 4. Определение этих функций содержится в следующей таблице.
Таблица значений и названий булевых функций от одной переменной:
|
x0=x |
|
1 |
|
0 |
|
Обозначение |
|
Название |
|
|
|
|
|
|||||
|
0 |
0 |
0 |
|
F1,0 = 0 |
|
тождественный ноль |
||
|
1 |
0 |
1 |
|
F1,1 = x = ¬x = x' = |
|
отрицание, логическое "НЕТ", "НЕ", "НИ", инвертор, |
||
|
|
NOT(x) |
|
SWAP (обмен) |
|||||
|
|
|
|
|
|
|
|
||
|
2 |
1 |
0 |
|
F1,2 = x |
|
тождественная функция, логическое "ДА", повтори- |
||
|
|
|
тель |
||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
1 |
|
F1,3 = 1 |
|
тождественная единица, тавтология |
||
существенные и фиктивные переменные,
еменная xi называется фиктивной (несущественной) переменной функции f(x1,···,xn), если
f(x1,···,xi-1,0,xi+1,···,xn) = f(x1,···,xi-1,1,xi+1,···,xn)
для любых значений x1,···,xi-1,xi+1,···,xn. Иначе переменная xi называется существенной.
IV. Теория графов. Основные понятия Мультиграф
Мультиграф — граф, в котором может быть пара вершин, которая соединена более чем одним ребром (ненаправленным), либо более чем двумя дугами противоположных направлений.
Псевдограф
Псевдограф — граф, который может содержать петли и/или кратные рёбра.
Орграф
G = (V,E) есть пара множеств, где V — множество вершин (узлов), E — множество дуг (ориентированных рёбер). Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v → w ведет от вершины v к вершине w, при этом вершина w смежная с вершиной v.
подграф
Подграф исходного графа — граф, содержащий некое подмножество вершин данного графа и некое подмножество инцидентных им рёбер
Смежность
понятие, используемое в отношении только двух рёбер либо только двух вершин: Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называютсясмежными
изоморфизм графов

Два графа называются изоморфными, если существует перестановка вершин, при которой они совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между их вершинами и рёбрами, которое сохраняет смежность и инцидентность (графы отличаются только названиями своих вершин).
. Удаление и добавление вершин ребер .
Матричные представления графов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Граф |
|
|
Матрица ин- |
|
|
Ориентирован- |
|
|
Матрица инцидентности |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
цидентности |
|
|
ный граф |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Матрицей инцидентности (инциденций) неориентированного графа называется матрица  , для которой
, для которой  , если вершина
, если вершина  инцидентна ребру
инцидентна ребру  , в противном случае
, в противном случае  .
.
Определение:
Матрицей инцидентности (инциденций) ориентированного графа называется матрица  , для которой
, для которой  , если вершина
, если вершина  является началом дуги
является началом дуги 
,  , если
, если  является концом дуги
является концом дуги  , в остальных случаях
, в остальных случаях  .
.
|
|
|
|
|
|
|
|
|
Граф |
Матрица смежности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Маршруты и связность.
Маршрут в графе — это чередующаяся последовательность вершин и рёбер  , в которой любые два соседних элемен-
, в которой любые два соседних элемен-
та инцидентны. Если  , то маршрут замкнут, иначе открыт.
, то маршрут замкнут, иначе открыт.
Связность. Две вершины в графе связаны, если существует соединяющая их
(простая) цепь.
Понятия: цепь
Цепь в графе — маршрут, все рёбра которого различны. Если все вершины (а тем самым и рёбра) различны, то такая цепь называется простой (элементарной). В цепи  вершины
вершины  и
и  называются концамицепи. Цепь с концами u и v соединяет вершины u и v. Цепь, соединяющая верши-
называются концамицепи. Цепь с концами u и v соединяет вершины u и v. Цепь, соединяющая верши-
ны u и v обозначается  . Для орграфов цепь называется орцепью.
. Для орграфов цепь называется орцепью.
цикл, простой цикл
Цикл — замкнутая цепь. Для орграфов цикл называется контуром.
Цикл (простой цикл) в орграфе — это простой путь длины не менее 1, кото-
рый начинается и заканчивается в одной и той же вершине.
компонента связности
некоторое подмножество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.
обхват, окружение
Обхват (англ.) — длина наименьшего цикла в графе.
Окружение — множество вершин, смежных с заданной.
Фактор. Степень вершины.
Степень вершины — количество рёбер графа G, инцидентных вершине x. Обозначается  . Минимальная степень вершины графа G обозначается
. Минимальная степень вершины графа G обозначается  .
.
амаксимальная —  .
.
n-Фактор графа — регулярный остовный подграф степени  .
.
Остовный подграф — подграф, содержащий все вершины.
Двудольный граф.
Двудольный граф или биграф — это математический термин теории графов, обозначающий граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части
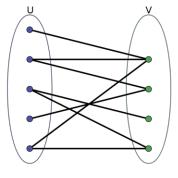
с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.
Точка сочленения.
вершина графа, в результате удаления которой вместе со всеми инцидентными ей рёбрами количество компонент связности в графе возраста-
ет.
Блок. Разрез.
множество ребер, удаление которого делает граф несвязным.
Деревья.
Дерево — связный граф, не содержащий циклов.
Сеть.
Граф в котором вершины как то помечены
Т. Менгера-Уитни.
3) Обходы графов. Эйлеровы графы. Гамильтоновы графы.
Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (ср. Гамильтонов путь)
Эйлеров цикл — это эйлеров путь, являющийся циклом. Эйлеров граф — граф, содержащий эйлеров цикл.
Кроме того, согласно теореме, доказанной Эйлером, эйлеров цикл существует тогда и только тогда, когда граф связный и в нём отсутствуют вершины нечётной степени.
Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.
Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом (см. Словарь терминов теории графов). Задача определения содержит ли данный граф гамильтонов цикл является NP-полной.
Если неориентированный граф G содержит гамильтонов цикл, тогда в нём не существует ни одной вершины x(i) с локальной степенью p(x(i)) < 2. Доказательство следует из определения.
