
mat.analiz_1
.pdf






|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A = lim f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число A називається границею функції |
f (x) |
при |
|||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x → ∞, якщо |
|
|
||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε > 0, δ =δ (ε ) > 0, |
|
(xn ): xn X , n N, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
f (x) → A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x : x X , |
|
|
|
|
|
|
|
|
|
|
xn → ∞ f |
(xn ) → A |
||||||
|
|
|
|
|
|
|
A +ε |
|
Y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
при x → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
( |
x |
) |
− A |
|
<ε |
|
|||||||||||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
x |
|
>δ |
|
|
|
n→∞ |
n→∞ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
A −ε |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
A = lim f (x) |
с−δ |
0 |
|
|
δс |
Число A називається границею функції |
f (x) |
при |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
x→+∞ |
|
|
|
|
A +ε |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x →+∞, якщо |
|
|
|||||||
або |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
ε > 0, δ =δ (ε ) > 0, |
|
x X ,n N, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
f (x) → A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
A−ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xn ): n |
|
|
||
при x →+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
x : x X , |
|
|
f |
( |
x |
) |
− A |
|
< ε |
|
xn > 0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
δ |
|
x >δ |
|
|
|
xn →+ ∞ f (xn ) |
→ A |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
n→∞ |
||||||
A = lim f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A +ε |
Число A називається границею функції |
при |
|||||||||||||||||||||
x→−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
x → −∞ , якщо |
|
|
||||||||
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A−ε X |
ε > 0, δ =δ (ε ) > 0, |
|
x X ,n N, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
f (x) → A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
с |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xn ): n |
|
|
||||
при x → −∞ |
|
|
|
|
|
|
|
|
−δ |
|
|
|
|
|
|
|
|
x : x X , |
|
|
f |
( |
x |
) |
− A |
|
< ε |
|
xn < 0, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x <δ |
|
|
|
xn →−∞ f (xn ) |
→ A |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
146

План:
1.Основні властивості границь функцій у точці.
2.Границя композиції функцій.
3.Таблиця “чудових границь”.
4.Нескінченно малі і нескінченно великі функції, порівняння нескінченно малих функцій. Еквівалентні функції.
Мета лекції: знати основні властивості границі функції в точці.
Основні властивості границь функцій у точці.
Будемо розглядати функції, визначені на множині X R, а точка
x0 є граничною точкою множини X |
(скінченною або нескінченно |
|||||||||||||||||
віддаленою). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема 12.1 (теорема про збереження знаку). Якщо функція |
||||||||||||||||||
y = f |
( |
x |
) |
|
|
|
|
0 |
|
x→x |
( |
x |
) |
= A і |
||||
|
|
має скінченну границю при x → x , тобто lim f |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
A > p |
(A < q), то x O* (x0 )∩ X : f (x)> p |
( f (x)< q). |
|
|
|
|
|
|
||||||||||
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim f (x)= A, |
|
A > p |
ε > 0 |
δ > 0 |
x Oδ* (x0 )∩ X |
|
f (x)− A |
|
< ε |
|||||||||
|
|
|
||||||||||||||||
x→x0 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
A −ε < f (x)< A +ε |
|||||||||
Виберемо |
число ε |
так, щоб |
p < A −ε < A . |
Тоді |
p < A −ε < f (x) |
|||||||||||||
x Oδ* (x0 )∩ X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теорема 12.2. Якщо функція y = f (x) в точці x0 |
має границю, то |
|||||||||||||||||
існує окіл точки x0 |
такий, що для будь яких значень x |
|
з цього |
|||||||||||||||
околу, крім можливо, |
x = x0 , множина значень f (x) є обмеженою. |
|||||||||||||||||
Доведення. Нехай
147

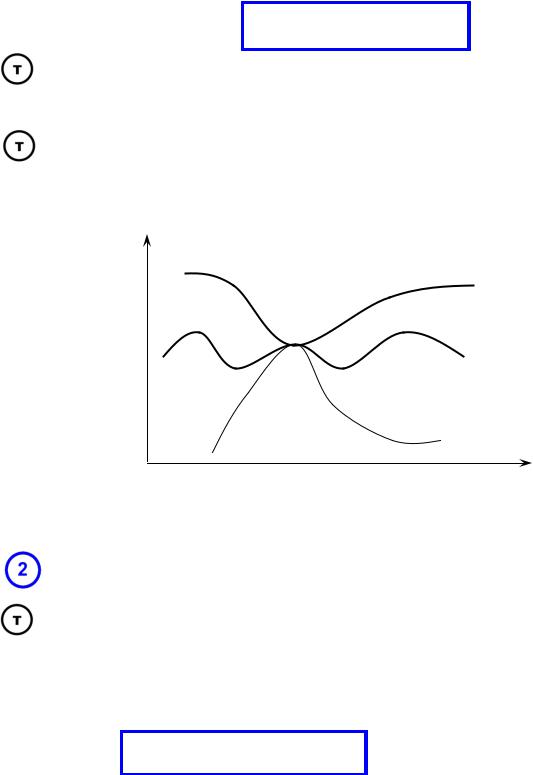


 Односторонні границі.
Односторонні границі. Означення 11.5 (за Коші).
Означення 11.5 (за Коші). 
 Означення 11.10.
Означення 11.10.