
Кіровоград олімпіади
.pdf
Мал. 82 |
|
|
|
|
10. 2 . Виконаємо рівносильні перетворення рівняння: |
|
|
||
|
|
[2x − 1] = k, |
||
[2x − 1]− [3 − x] = 2 [2x − 1] = [5 − x] [5 − x] = k, |
||||
|
|
k , |
|
|
|
k + 1 |
≤ x < |
k + 2 |
. |
k ≤ 2x − 1< k + 1, |
2 |
2 |
||
k ≤ 5 − x < k + 1, 4 − k < x ≤ 5 − k, |
|
|||
k , |
k . |
|
|
|
|
|
|
|
|
Необхідною умовою існування розв’язків останньої системи нерівностей з цілим параметром k є нерівності k 2+ 1 ≤ 5 − k і 4 − k < k +2 2 . Звідси знаходимо
k = 3. З останньої системи нерівностей дістаємо x = 2. |
11. Ні, не може. Нехай |
|||||||
n – кількість членів |
|
гуртка, x – кількість |
хлопчиків у гуртку. Нескладно |
|||||
переконатися, що x > |
|
91 |
n, n ≥ 200 . Тому x > |
|
91 |
200 |
> 20. 12. Вказівка. Для |
|
100 |
100 |
|||||||
|
9 |
9 |
|
|||||
доведення скористайтесь формулою
a2n+1 + b2n+1 = (a + b)(a2n + a2n−1b + ... + ab2n−1 + b2n ),
яка має місце для всіх дійсних чисел a, b і натуральних чисел n . 13. Рівняння
рівносильне рівнянню |
|
(2x)3 + (x + 2)3 |
= 0. |
Тому |
x = − |
2 . |
14. Нехай |
|||
a + b = c, ab = d . Тоді |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
c |
≥ |
d |
|
c 2 |
≥ |
|
d |
|
|
|
2 − c |
1− c + d |
|
|
1 |
− c + d |
|
|
|||
|
2 |
− c |
|
|
|
|
||||
|
|
|
161 |
|
|
|
|
|
|
|

(c2 − 4d)(1− c) ≥ 0 (a − b)2 (1− a − b) ≥ 0. |
|
|
|
|
|
Одержана нерівність очевидна. Розглянемо рівність |
|
|
|
|
|
(a − b)2 (1− a − b) = 0 a − b = 0, |
a = b, |
|
|
|
|
|
1 |
. |
|
|
|
1− a − b = 0 |
a = b = |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
Отже, нерівність перетворюється в рівність тільки тоді, коли a = b 0; |
1 |
. |
|||
|
|
|
|
2 |
|
15. Перенесемо всі доданки з правої частини рівності в ліву, додамо й віднімемо вираз x2 y2 z2 і розкладемо на множники: (x2 − yz)(y2 − zx)(z2 − xy)= 0. Якщо один з множників, наприклад перший, дорівнює нулю, а всі інші відмінні від нуля, то x ≠ y ≠ z . Тому x2 – площа квадрата, довжина сторони якого дорівнює x , а yz – площа прямокутника, довжини сторін якого дорівнюють y і
z . Якщо два множники дорівнюють нулю, то й третій дорівнюватиме нулю, а x = y = z. У цьому випадку прямокутник вироджується у квадрат. 16. Якщо α –
гострий кут трикутника, b – довжина прилеглого катета, то довжина шляху дорівнює 2bsinα , а отже, не залежить від стартового положення кулі на гіпотенузі. 17. Кут BCA більший за кут DCA . Справді, з умови випливає, що DC > BC , оскільки проекція DC на BD більша за DE ( E – середина BD ), а проекція BC менша за BE . Зважаючи на те, що площі трикутників BCE і DCE однакові, відстань від E до BC більша за відстань від E до CD , тому кут BCE більший за кут DCE . (Останній не може бути тупим). 18. Шукані
значення |
параметра |
m |
визначаються |
умовами: |
m > 0 |
та |
||
(m − 2)2 − 4m(3 − 2m) = 0 |
і дорівнюють |
8 ± 2 7 |
. 19. Зрозуміло, що хорд більше |
|||||
|
|
|
|
9 |
|
|
|
|
семи, бо довжина кожної хорди не перевищує 2. Сумарна довжина всіх дуг, що стягують ці хорди, більша за 7 2π . Тому на колі знайдеться точка, що покривається щонайменше вісьмома дугами. Діаметр, проведений з цієї точки, перетне не менше восьми хорд.
Х КЛАС
1. ± 4 36 ; m 496 . 2. Якщо пара цілих чисел x і y є розв’язком рівняння, то
ці числа повинні бути одночасно або парними, або непарними. В обох випадках ліва частина рівняння ділитися без остачі на 4. Оскільки 2002 на 4 без остачі не ділиться, то рівняння не має цілих розв’язків. 3. Нехай пряма l , що паралельна заданій прямій, має з параболою єдину спільну точку P , а Q – основа
перпендикуляра, опущеного з точки P на задану пряму (мал. 83). Очевидно, що відрізок PQ – шуканий. Обчислимо його довжину. Для цього визначимо
162

координати точок P і Q . Координати точки P дістанемо, знайшовши єдиний розв’язок системи рівнянь
|
|
|
|
2 |
, |
|
2 |
− x − b = 0, |
|
|
|
|
|
y = x |
|
x |
|
|
|
||
|
|
1 |
y = x + b, |
y = x + b. |
1 |
|
||||
Якщо |
b = − |
, то перше рівняння системи має єдиний розв’язок x = |
, а |
|||||||
|
|
4 |
|
|
|
|
|
|
2 |
|
система – єдиний розв’язок: 12 ; 14 . Ці числа є координатами точки P .
Нескладно переконатися, що y = − x + 34 – рівняння прямої PQ , а 78 ; − 18 –
координати точки Q . Далі обчислюємо PQ = 3 82 .
Мал. 83 |
Мал. 84 |
Зауважимо, довжина відрізка PQ дорівнює відстані d точки P(a, b) до прямої
Ax + By + C = 0 , яка обчислюється за формулою d = aA + bB + C . 4. Нехай
A2 + B2
трикутник ABC такий, що точка O – середина сторони BC , а AMN – довільний трикутник (мал. 84). Доведемо, що трикутник ABC має найменшу площу. За властивістю площі маємо рівності
SABC = SABON + SCON , SAMN = SABON + SBOM .
Якщо точка N лежить між точками A і C , то нескладно переконатися, що
ON < OM . Тому
SCON |
= 1 ON OC sinϕ ≤ 1 OM OBsinϕ = SBOM , |
|
|
2 |
2 |
а SABC ≤ SAMN . Для побудови точок B і C потрібно на промені AO побудувати |
||
точку D так, щоб |
AO = OD , і |
провести через точку D прямі, паралельні |
сторонам даного кута. У перетині дістанемо точки B і C . 5. Позначимо даний
163
многочлен через |
Pk (x) . Нехай k = 2m − 1. Тоді многочлен має парну кількість |
|||||||||||||||||||||||||
одночленів, які згрупуємо попарно. |
|
|
|
+ ... + (C2m−2 |
− C2m−1x)x2m−2 . |
|
||||||||||||||||||||
|
P |
(x) = (1− C1 x)+ |
(C |
2 − C3 x)x2 |
|
|||||||||||||||||||||
|
|
2m−1 |
|
|
|
|
|
|
n |
|
|
|
n |
n |
|
|
|
n |
|
|
|
n |
|
|
||
Встановимо знак кожної різниці для |
x 0, 1 . |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 = 0; |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1− Cn1 x = 1− nx ≥ |
1− n |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
Cn2 − Cn3 x = n(n − 1) − n(n − 1)(n − 2) x = n(n − 1) |
(3 − (n − 2)x) ≥ |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
3! |
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
≥ n(n − 1) 3 − |
(n − |
2) 1 |
= 2(n + 1)(n − 1) ≥ 0; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
n |
|
3! |
|
|
|
|
|
|
||
|
|
………………………………………………………………. |
|
|||||||||||||||||||||||
Cn2m−2 − Cn2m−1x = n(n − 1) ... (n − 2m + 3) |
− n ... (n − 2m + 3)(n − 2m + 2) x = |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(2m − 2)! |
|
|
|
|
|
|
(2m − 1)! |
|
|
||||||
|
|
|
= n(n − 1) ... (n − 2m + 3) (2m − 1− (n − 2m + 2)x) ≥ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(2m − 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
≥ n(n − 1) ... (n − 2m + 3) |
2m − 1− (n − 2m + |
2) 1 |
= |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
(2m − 1)! |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||
|
|
|
|
|
|
= 2(m − 1)(n + 1)(n − 1) ... (n − 2m + 3) ≥ 0 . |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2m − 1)! |
|
|
|
|
|
|
P2m−1(x) ≥ 0 |
|
||||
З урахуванням |
отриманих |
нерівностей |
маємо |
нерівність |
для |
|||||||||||||||||||||
x 0, 1 . Якщо k = 2m , |
то |
P |
|
(x) = P |
|
(x) + C2m x2m |
≥ 0. Отже, P (x) ≥ 0 |
для |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2m |
|
|
2m−1 |
|
n |
|
|
|
|
|
k |
|
||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
всіх |
x 0, |
1 |
і |
k = 1, 2, ..., n . |
6. |
|
Побудуємо рекурентну послідовність (x ) , у |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
якої |
x ≠ 2 , |
а |
x |
|
= |
|
|
|
для |
n = 1, 2, .... |
Виразимо всі члени послідовності, |
|||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
n+1 |
|
|
2 |
− xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
починаючи з другого, через x1 |
|
|
|
|
|
2x1 − 4 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x2 |
= |
|
4 |
|
, x3 |
= |
|
4 |
|
= |
, x4 |
= |
|
4 |
|
= x1. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x1 |
2 − x3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 − x1 |
|
2 − x2 |
|
|
|
|
|
|
|
|||||||||
Зрозуміло, що побудована послідовність є періодичною послідовністю з періодом 3. Нехай функція f – розв’язок рівняння. Тоді для
x = x1, x = x2 , x = x3 виконуються такі рівності:
164
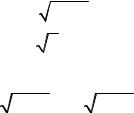
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f |
(x1) + f |
|
|
|
|
|
= x1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 − x1 |
|
|
f |
(x1) + f (x2 ) = x1, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f |
(x ) + f |
|
|
|
|
|
= x , |
f |
(x |
) + f (x |
) = x |
, |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
− x2 |
|
|
f |
(x |
) + f (x |
) = x . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
f |
(x ) + f |
|
|
|
|
|
= x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3 |
2 |
− x |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
(x1 − x2 + x3 ) |
|
|
|
|
1 |
|
|
|
|
|
4 |
|
2x1 − 4 |
|
|||||||||
Звідси знаходимо |
f (x1) |
= |
|
|
або |
f (x1) = |
|
x1 |
|
− |
|
|
|
|
+ |
|
|
. |
|||||||||
2 |
2 |
2 |
− x1 |
x1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
2x − 4 |
|
|
||||
Перевіркою встановлюємо, |
що |
функція |
|
f (x) = |
|
x − |
|
|
|
|
|
+ |
|
|
|
є |
|||||||||||
|
|
|
2 − x |
|
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
розв’язком рівняння. 7. Ліва частина рівняння є квадратним тричленом відносно параметра a . Тому рівняння запишемо так:
a2 − 2a(x2 − 5x − 1) + (x4 − 10x3 + 22x2 + 12x) = 0.
Оскільки його дискримінант невід’ємний: D = (x − 1)2 ≥ 0 , то маємо рівняння a2 + 10a + 25 = 0, якщо x = 1, і (a − x2 + 6x)(a − x2 + 4x + 2) = 0 в іншому разі. У
першому випадку a = −5 і дане рівняння набуває вигляду
x4 − 10x3 + 32x2 − 38x + 15 = 0 (x − 1)2 (x − 3)(x − 5) = 0 .
Звідси маємо 4 корені рівняння: |
1,1, 3 і 5. У випадках, коли a ≠ 5 маємо |
сукупність квадратних рівнянь |
x2 − 6x − a = 0 і x2 − 4x − 2 − a = 0, яку |
пропонуємо розв’язати самостійно. Розв’язки даного рівняння, залежно від
параметра, наведеніaнижче. |
|
x |
(−∞; − 9) |
розв′язків немає |
|
− 9 |
3; 3 |
|
(−9; − 6) |
3 ± |
9 + a |
− 6 |
3 ± |
2, 2, 2 |
− 5 |
1,1, 3, 5 |
|
(−6; − 5), (−5; + ∞) |
3 ± 9 + a, 3 ± 6 + a |
|
8. Шуканий двогранний кут A, BD1,C1 |
і двогранний кут A, BD1,C – суміжні |
|
(мал. 85). Тому сума їх лінійних кутів дорівнює 180° . Визначимо лінійний кут α двогранного кута A, BD1,C . У гранях цього кута містяться рівні прямокутні
трикутники BAD1 і BCD1 . Якщо AM BD1 , то CM BD1 . Тому AMC = α – лінійний кут двогранного кута A, BD1,C . За теоремою косинусів
cosα = |
AM 2 |
+ MC2 |
− AC2 |
= |
2AM 2 |
− 2a2 |
, |
|
2AM MC |
2AM 2 |
|||||||
|
|
|
||||||
|
|
|
165 |
|
|
|
|
|

|
|
|
4 |
2 |
|
|
2 |
|
|
|
|
де a – ребро куба. Оскільки AM 2 = |
2 a2 |
, |
то cosα = |
3 a |
|
− |
2a |
|
= − |
1 |
. Тому |
|
4 |
|
|
|
2 |
||||||
|
3 |
|
|
|
a |
2 |
|
|
|
||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α = 120° , а шуканий кут дорівнює 60° .
Мал. 85 |
Мал. 86 |
9. Доведення нерівності проведемо способом послаблення з залученням співвідношення між середнім арифметичним і середнім геометричним та властивістю модуля дійсного числа.
3 |
(a4 |
+ b4 + c4 )+ 24 = a4 + 16 + b4 + 16 + c4 + 16 |
|
|
+ a4 |
+ b4 + c4 |
≥ |
|
||||||||||||||||||
2 |
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≥ 16a4 + 16b4 + 16c4 + a4 + b4 + c4 = |
|
|
|
|
|
|
|
4 |
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
4 |
|
+ 4b |
2 |
|
|
|
4 |
+ 4c |
2 |
|
|
||||||
= 4a2 + |
4b2 + 4c2 + a4 + b4 + c4 = 2 4a |
|
+ c |
|
|
|
|
+ a |
|
|
+ b |
|
≥ |
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||
|
≥ 2( |
4a2c4 + 4b2a4 + 4c2a4 |
)= 4( |
|
a |
|
c2 + |
|
b |
|
a2 + |
|
a |
|
b2 ) ≥ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
≥4(ac2 + ba2 + cb2 ).
10.Виконаємо наступні рівносильні перетворення рівняння:
(xy)2 + (yx)2 = 2005 ((10x + y) + y)2 + ((10y + x) + x)2 = 2005
99(x2 − y2 ) = 2005.
Одержане рівняння не має цілих розв’язків, бо його права частина не ділиться
без остачі на 99. 11. Оскільки |
|
|
|
|
|
|
|
y − x |
|
|||
1 |
≥ |
1 |
|
1 |
− |
1 |
≥ |
1 |
|
≥ 0 , |
||
x |
y |
x |
y |
y |
xy |
|||||||
|
|
|
|
|
|
|||||||
то дана нерівність рівносильна такій сукупності систем нерівностей:
166

|
x ≤ y, |
|
|
xy > 0, |
|
|
x ≥ y, |
|
|
|
xy < 0. |
|
|
|
|
|
|
Множину точок, координати яких задовольняють нерівності систем сукупності
зображено |
на мал. |
86. |
12. Нехай |
k > 1 – |
натуральне число |
таке, що |
|||||||||||
3n + 5n |
= k(3n−1 + 5n−1) . |
Тоді |
рівність |
5n−1(5 − k) = 3n−1(k − 3) |
|
може |
|
|
виконуватися |
||||||||
тільки |
за |
умови, |
що |
k = 4 , а |
5n−1 = 3n−1 . |
Звідси |
|
n = 1. |
13. |
Оскільки |
|||||||
P(x, y) = P(− x, y) = P(x, − y) = P( y, x) , |
де P(x, y) = |
|
x + y |
|
+ |
|
x − y |
|
, |
то задана |
|||||||
|
|
|
|
||||||||||||||
множина точок симетрична відносно координатних осей і бісектрис координатних кутів. Якщо 0 ≤ y ≤ x , то x ≤ 1, і множина точок, координати
яких задовольняють |
нерівність 0 ≤ y ≤ x ≤ 1, |
є трикутником |
з вершинами |
в |
|||||||
точках (0; 0) , (1; 0) і |
(1;1) . Тому нерівність |
|
x + y |
|
+ |
|
x − y |
|
≤ 2 |
задає квадрат зі |
|
|
|
|
|
||||||||
стороною 2 (мал. 87), а його площа дорівнює |
4. 1− 2x + 2x2 набувають в точці |
1 . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
Мал. 87 |
|
|
Мал. 88 |
||
14. Позначимо вираз через P(x, y) . З урахуванням |
умови x + y = 1 він |
||||
запишеться так: |
|
|
1 |
|
|
P(x,1 − x) = 1 − 3x + 3x2 − |
|
|
. |
||
1 |
− 2x + 2x2 |
||||
|
|
||||
Різниця буде найменшою, якщо одночасно зменшуване найменше, а від’ємник
– найбільший. Найменше |
значення |
квадратні |
тричлени 1 − 3x + 3x2 і |
|||||||
1− 2x + 2x |
2 |
|
1 |
|
1 |
|
1 |
|
3 |
|
|
набувають в точці |
2 |
. Тому P |
2 |
, |
2 |
= −1 |
4 |
– найменше значення. |
|
15. Поділимо першу рівність на xy , другу – на yz і одержані рівності додамо:
167


з якої нескладно знайти f (t) = 40111 (t2 + 4010t − 2005) . Перевірка підтверджує правильність визначення функції. 19. Складемо куб довільним чином. Нехай на
його поверхні буде |
a білих і b чорних квадратів. |
Зрозуміло, що |
a + b = 24 . |
Розглянемо число |
x = a − b . Воно парне. Якщо |
x = 0 , то a = b , |
і задача |
розв’язана. В іншому разі поворот одного з кубиків на кут 90° відносно однієї з осей, що проходить через центри протилежних граней, залишає число x незмінним або змінює його на 2. За три такі операції можна досягти, щоб грані кубика, які були на поверхні куба сховалися всередину, а ті, що були всередині,
опинилися на поверхні. За 24 |
такі |
операції |
число x дорівнюватиме |
(24 − a) − (24 − b) = b − a = −(a − b), |
тобто |
стане |
протилежним початковому |
значенню. Отже, на якомусь кроці воно дорівнюватиме нулю. |
|||
|
|
|
|
ХІ КЛАС |
|
|
||||
1. −7, − 3. |
Вказівка: Виконайте заміну: x + 5 = t . 2. Помножимо другу |
|||||||||
рівність на 2 і віднімемо від першої. |
|
|
||||||||
|
|
x2 + y2 + z2 − 2xz + 2xy − 2yz = 0 (x + y − z)2 = 0 z = x + y . |
||||||||
Після цього з другої рівності дістанемо |
|
|
||||||||
|
|
|
|
x2 + xy + y2 = 4 y2 + xy + (x2 − 4) = 0. |
||||||
Здобута рівність може виконуватися тільки за умови, що |
||||||||||
|
|
|
|
x2 − 4(x2 − 4) ≥ 0 3x2 ≤ 16 |
|
x |
|
≤ |
4 |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
||||
3. Вказівка: дивись задачу 6 для Х класу. 4. n + 2. 5. ± |
|
|||||||||
2. Уведемо нову змінну |
||||||||||
t = 3x − |
π |
, 3π |
|
і знайдемо ті значення параметра m , для яких рівняння |
||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
cos2 t + (2m2 − 3,5)cost + m2 − 2 = 0 |
||||||
на проміжку − |
π |
, 3π має точно 5 розв’язків. Нескладно переконатися, що це |
||||||||
|
|
|
2 |
2 |
|
|
||||
рівняння рівносильне такій сукупності рівнянь:
cost = − 12 ,
cost = 4 − 2m2.
Далі вдамося до графічного способу розв’язування рівнянь. Для цього
побудуємо графік функції y = cost на проміжку |
− |
π |
, |
3π |
(мал. 89). Перше |
|
|
2 |
|
2 |
|
рівняння сукупності на цьому проміжку має два розв’язки 56π і 116π . Тільки за
169

