Кіровоград олімпіади

Аналогічно доводиться, що CE KD, AD EK. 9. Нехай 11...1 = a. Тоді

{

n

11...1− 22...2 = 10n a + a − 2a = 10n a − a = (10n − 1)a =

{

123

2n

n

= 99...9a =

9a2 = 3a = 33...3.

123

123

n

n

x + y

≥ xy, x ≥ 0, y ≥ 0,

2

x + y 2

2

рівність досягається тільки за умови, що x = y . Тому

2003

xy ≤

=

2

, а

2

2003

2

x = y =

2003

. 13. Ні, не можна. Для розв’язання задачі

xy =

2

, якщо

2

кожного множника застосуємо нерівність Коші:

yz 2 zx 2 xy = 8xyz.

(a − x)(a − y)(a − z) = ( y + z)(z + x)(x + y) ≥ 2

3. Нехай a, b, c – сторони трикутника

ABC ,

ma , mb , mc – його медіани. На

продовжені медіани CN побудуємо точку P так, щоб PM = MC (мал. 34).

Чотирикутник AMBP – паралелограм. Тому

AB2 + MP2 = 2(AP2 + BP2 ).

С

K

M

L

A

N

В

P

Мал. 34

Звідси знаходимо сторону

c трикутника:

c = 2

2m2

+ 2m2

− m2

. Аналогічно

3

a

b

c

можна встановити, що b = 2

2m2

+ 2m2

− m2

, a = 2

2m2

+ 2m2

− m2 .

3

c

a

b

3

b

c

a

де p – ціле число. Далі знаходимо цілі невід’ємні розв’язки

рівняння:

m = 1− 5 p, n = 19 + 8 p, p = −2, − 1, 0. Звідси маємо суму m + n = 20 + 3p,

яка буде

центри яких містяться в точках (−1; 0) і (1; 0) . 7. Утворимо систему рівнянь і

розв’яжемо її:

(1− 2a)x2 − 6ax − 1 = 0,

a(2x2 + 6x) = x2

− 1,

ax2 − x + 1 = 0,

ax2 = x − 1.

x2

− 1

=

x − 1

,

2x2

+ 6x

x2

значення параметра a : − 3 , 0,

2 .

4

9

8.

xy + x = a2 − b2 x( y + 1) = (a − b)(a + b)

x = a − b,

a = 1+ x + y , b =

1− x + y .

y + 1 = a + b,

2

2

9. Нехай бісектриса кута B перетинає коло в точці N (мал. 35). Тоді висоти

трикутника

DNE і відповідні бісектриси трикутника

ABC лежать на прямих

N

C

M

E

a

b

K

c

d

M

A

B

Q

A

P

B

D

N

Мал. 35

Мал. 36

10. 0. Оскільки 3a − 1 ≠ 0, x + x

= −1, x x

=

a2

, то, використовуючи рівності

2

2

1

1

3a − 1

(x + x

)3

= x3 + x3

+ 3x x

(x + x

), x3

+ x3 = −1,

1

2

1

2

1

2

1

2

1

2

легко знайти шукані

значення

параметра

a.

11.

4006. Графіком рівняння

не змінюється. 12. 7,5r2 . Трикутник AMB прямокутний, тому

a2 + b2 = 4r2

(мал. 36). Чотирикутник AMBN – паралелограм, тому c2 + d 2 = r2

+ 4r2

. Далі

x2

− 2x,

якщо

x < −1,

y = x2

+ 2,

якщо − 1 ≤ x ≤ 1,

x2

+ 2x,

якщо

x > 1.

2. Якщо

M – точка перетину медіан трикутника ABC (мал. 37), то

BDM –

прямокутний рівнобедрений трикутник: DB = DM = 1 м. За властивістю медіан

трикутника маємо CD = 3 м і CD AB . Тому площа трикутника дорівнює 3 м2 .

3. a2 + b2 > 3 a3 + b3

( a2 + b2 )6 > (3 a3 + b3

)6 (a2 + b2 )3 > (a3 + b3 )2

3a4b2 + 3a2b4 > 2a3b3 3a2 + 3b2 > 2ab (a − b)2 > − 4ab .

3

C

D

C

M

A 60°

30°

L

B

x

K

A

D

B

Мал. 37

Мал. 38

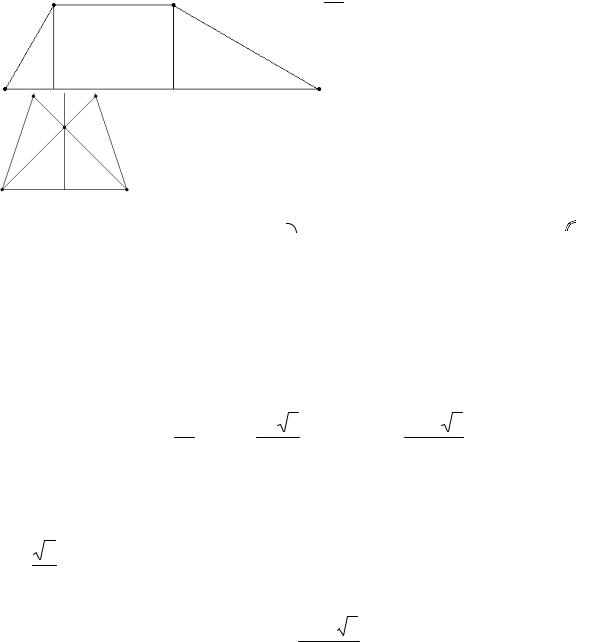
4. Нехай DK = CL = h – висота трапеції,

AK = x, LB = 54 − x (мал. 38). Тоді

xtg60° = h = (54 − x)tg30° .

Далі знаходимо x =

27

см, h = 27 3 см

і

S = 1377 3 см2 .

5.

Рівняння

2

2

2

(мал. 39).

Вони мають єдину спільну точку A(x1; y1 ). Абсциса цієї точки є

розв’язком рівняння. Тому x2 + 2[x1 ] = 2.

Оскільки − 2 < x < −1,

то [x ]= −2 , а

1

1

1

x = − 7 . 6. Розкладемо ліву частину рівняння на множники:

1

2

(x − 1)(x2 + x − 1)= 0.

Звідси знаходимо корені рівняння: 1,

− 1±

5 . 7. За властивістю цілої частини

2

[

x

− 1]= [

x

]− 1. Тому

y

= [

x

]− 1. Оскільки

модулі протилежних чисел рівні:

− x

=

x

,

− y

=

y

, то

графік рівняння

симетричний відносно

координатних

осей. Тому побудуємо його спочатку

в першому координатному куті. Для

x ≥ 1, y ≥ 0

рівняння набуває вигляду

y = [x]− 1. Продовжуючи графік функції

y = [x]− 1

симетрично відносно координатних осей на всю

координатну

y

4

y = 2x

y

2

3

y = 2[x]

1

y = 2 − x2

2

-4

-3

-2

-1

0

1

2

3

4

x

1

A

-1

-2

-1

0

1

2

x

-2

Мал. 39

Мал. 40

8. Якщо a, b (a < b) – катети, c – гіпотенуза трикутника,

d – різниця прогресії,

то b = a + d, c = a + 2d

і a2 + b2 = c2 . Далі знаходимо:

a = 3d, b = 4d, c = 5d .

Нарешті, використовуючи формули для обчислення площі трикутника S =

1 ab

і S = a + b + c r , встановлюємо, що d = r.

2

9. Нехай a, b, c – сторони трикутника,

2

x, y, z – відстані центра до сторін відповідно,

R – радіус описаного кола. Тоді

S = x + y + z =

R2 − a2

+

R2 − b2 +

R2 − c2 =

4

4

4

= R − a

R + a

+ R − b

R + b + R − c

R + c .

2

2

2

2

2

2

Для відшукання найбільшого значення суми S скористаємося нерівністю

Коші-Буняковського:

R − a

R + a

+ R − b

R + b

+ R − c

R + c

≤

2

2

2

2

2

2

≤ R − a

+ R − b + R − c

R + a

+ R + b

+ R + c

=

2

2

2

2

2

2

3R − p

3R + p = 9R2 − p2

2

2

4

У цьому співвідношенні рівність матиме місце за такої умови:

R

−

a

R

−

b

R −

c

2

=

2

=

2 .

R

+

a

R

+

b

R +

c

2

2

2

sin2 x + sin2

sin2

x = 1,

x =

π

+ kπ , k = 0,1, 2, ... ,

y = 2

2

sin2

y = 1

y =

π

+ nπ , n = 0,1, 2, ... .

2

Якщо xy < 0, то

sin

2 x + sin2 y =

0

sin2

x = 0,

x = kπ ,

y = 0

y = nπ , k, n Z, kn < 0 .

sin2

Для від’ємних x

і

y

дана рівність не виконується. 11.

1±

5 ,

− 3 ± 13 . Треба

2

2

спочатку поділити обидві частини рівняння на x2 , а потім,

використовуючи

заміни x − 1

= t

і

x2 +

1

= t2 + 2 ,

звести рівняння до квадратного. 12. Нехай

x2

x

a, b, c – сторони трикутника, ma , mb , mc

– відповідні медіани. Тоді

m = 1

2b2 + 2c2 − a2 , m = 1

2a2 + 2c2 − b2 , m = 1

2b2 + 2a2 − c2 .

a

2

b

2

c

2

Тому

= 1 ((2b2 + 2c2 − a2 )+ (2c2 + 2a2 − b2 )+ (2a2 + 2b2 − c2 ))=

m2

+ m2

+ m2

a

b

c

4

3

(a2 + b2 + c2 ).

=

4

Далі скористаємося нерівністю Коші-Буняковського:

3(a2 + b2 + c2 )= (12 + 12 + 12 )(a2 + b2 + c2 )≥ (1 a + 1 b + 1 c)2 .

m

2

+ m

2

+ m

2

p

2

13. У кожній

Насамкінець

маємо:

a

≥

.

парі «дівчинка –

b

c

2

загальності, можна вважати, що A, B α (мал. 41). Тоді ABC1D1

і ABC2 D2 –

паралелограми. Позначимо площину DCC1D1 через γ1, а DCC2 D2

– γ2. Площини

C

C3

D

C

D

C1

α

P

B

C1

D1

B1

B2

D1

B

α

A

C2

A

C2

D2

D2

Мал. 41

Мал. 42

2) У цьому

випадку будемо

вважати, що A α,

AB1C1D1

і AB2C2 D2 –

BB1 A, γ2 – площина CC2 D2 , β2

–

площина

BB2 A .

Тоді γ1||β1

і γ2||β2, а

DC = γ 1 ∩ γ 2 ,

AB = β1∩β2, при

цьому

AB || DC .

(Якби

AB і DC

були

не

паралельні, то

AB перетинала

б

або γ1, або γ2). Якщо

точка C3

така,

що

C2C3 = DD2 ,

то

∆ DCC3 = ∆ABB2 .

Тому DC = AB ,

а

отже,

ABCD

–

паралелограм.

1

A

B

0

1

x

D

C

Мал. 43

Мал. 44

1.

Див. малy. 43.(2; 3), [3; 7), [7; + ∞). 2. 45°. 3.

43

,

105 − 1 . Вказівка.

19

2

Розв’яжіть рівняння на проміжках 4. З рівностей x1 + x2

= a й x1 x2

= a − 1 маємо

x2

+ x2

= (a − 1)2 + 1 ≥ 1.

Тому

найменше значення виразу

x2

+ x2

дорівнює 1 і

1

2

1

2

відповідно, AB = DC = 16, AD = BC = 22, SO = 4

(мал. 45). На прямій SO

побудуємо точку S′

так,

щоб SO = OS′ .

Тоді

за властивостями діагоналей

паралелограма матимемо систему рівностей:

S′S 2

+ BD2

= 2( y2

+ v2 ),

2S′S 2 + BD2

+ AC2

= 2( y2 + v2 + x2 + u2 )

′ 2

+ AC

2

= 2(x

2

+ u

2

),

S S

y2 + v2 + x2

+ u2 = 804.

перший

член,

а

y = x + d, u = x + 2d, v = x + 3d ,

то приходимо

до

такого

діофантового рівняння:

+ (x + 3d )2 = 804 2x2 + 6dx + 7d 2 = 402

x2

+ (x + d)2 + (x + 2d)2

d

7d 2 < 402 d < 8.

Оскільки

–

парне число,

то

воно може дорівнювати

тільки

2, 4

або 6.

Перевіркою

встановлюємо,

що

d = 2 . Після

цього

знаходимо:

x = 11,

y = 13, u = 15, v = 17.

9. Після нескладних рівносильних перетворень матимемо

рівняння:

(sin x + sin y)(sin x − sin y)2

= 0

sin2

x − sin2 y = 0 cos 2x = cos 2y y = ± x + kπ , k Z.

S

y

D

2π

π

A

O

C

-2π -π

π

2π

x

B

-π

S'

-2π

Мал. 45

Мал. 46

10. Нехай

sin x + sin 3x + sin 5x + ... + sin 2003x = A . Помножимо рівність на

2sin x ≠ 0 і виконаємо перетворення:

2Asin x = 2(sin x + sin 3x + sin 5x + ... + sin 2003x)sin x

2Asin x = 1− cos 2004x.

Оскільки за

умовою 1− cos 2004x = 2sin x , то 2Asin x = 2sin x.Звідси маємо

11.

З

формули

Герона

маємо рівність

S 2 = p( p − a)( p − b)( p − c) . Оскільки

згідно з нерівністю Коші для трьох параметрів

( p − a) + ( p − b) + ( p − c) 3

( p − a)( p − b)( p − c) ≤

3

,

то

S 2

≤ p3 S ≤

p2 S ≤ (a + b + c)2 .Далі застосуємо нерівність Коші-

p

27

3 3

12 3

Буняковського

(a + b + c)2 = (1 a + 1 b + 1 c)2 ≤ (12 + 12 + 12 )(a2 + b2 + c2 ) = 3(a2 + b2 + c2 ) .

Тому S ≤ a2 + b2 + c2

. 12.

a

− 2; 3 −

21

1; 3 +

17

. За допомогою

4 3

2

2

похідної встановлюємо, що

x = ±1 – точки екстремумів, а

f (−1) = a2

− 3a − 2 і

f (1) = a2 + a − 2 – екстремуми функції. Якщо a > 0 , то f (−1)

– мінімум, який є і

найменшим значенням функції

f

в області її визначення; f(1) – максимум –

найбільше значення f, тобто

[f (−1); f (1)] – множина значень функції

f. Тому

для розв’язання задачі треба розв’язати таку систему нерівностей:

a > 0,

a2 − 3a − 2 ≤ 0,

a2

+ a − 2 ≥ 1.

Її розв’язками будуть

a 1; 3 +

17 . У разі, коли a < 0 ,

приходимо до

2

наступної системи нерівностей:

a < 0,

a2 − 3a − 2 ≥ 1,

a2

+ a − 2 ≤ 0.

2;

3 −

21

x, v = f (u),

з якої знаходимо a −

2

. 13. Уведенням змінних u =