7.2. Функциональные ряды

Рассмотрим ряд , члены которого являются функциями переменной х. Такие ряды называются функциональными. Ограничимся рассмотрением двух наиболее употребительных видов функциональ­ных рядов - степенных и тригонометрических.

Интервал сходимости. Функциональный ряд вида

,

(7.17)

где — постоянные вещественные числа, называется степенным рядом. Иногда рассматривают степенной ряд более общего вида

,

(7.18)

где — некоторое постоянное число.

Ряд (7.18) приводится к виду (7.17), если положить,

поэтому в дальнейшем будем рассматривать только ряды вида (7.17).

При каждом конкретном значении ряд (7.17) становится числовым. Поэтому при каких-то значениях этот ряд сходится, а при других – расходится. Множество значений , при которых

функциональный ряд сходится, называется областью сходимости ряда.

Можно доказать [ ], что для каждого степенного ряда су­ществует положительное число , такое, что этот ряд абсолютно сходится при и расходится при . Число называется радиусом сходимости рассматриваемого ряда, а интервал называется интервалом сходимости этого ряда.

На концах интервала сходимости (в точках и ) степенной ряд может сходиться или расходиться. Этот вопрос

решается для каждого числового ряда, получающегося из степенного ряда в результате подстановки в него указанных значений.

Очевидно, всякий степенной ряд (7.17) сходится при = 0. Может оказаться, что ряд сходится только при = 0, в этом случае . Может также оказаться, что ряд вида (7.17) схо­дится на всей числовой прямой, тогда .

В простейших случаях радиус сходимости степенного ряда (7.17) можно определить с помощью признака Даламбера или радикального признака Коши. Указанные признаки применяются к рядам с положительными членами, поэтому можно использовать только для ряда, составленного из абсолютных величин ряда (7.17):

,

(7.19)

Рассмотрим применение признака Даламбера. Пусть существует предел

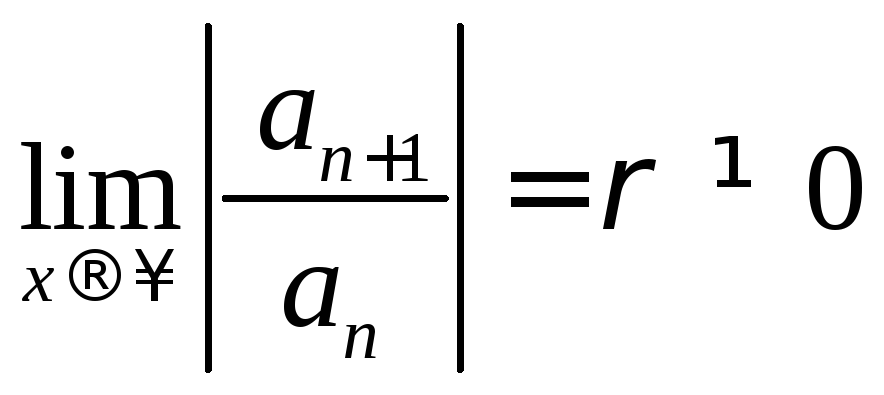. Применим признак Даламбера к ряду (7.17)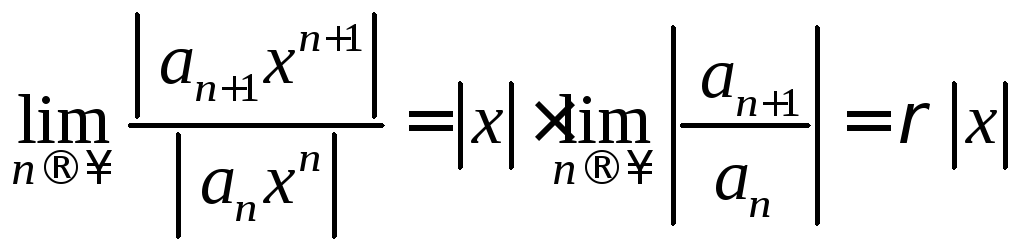

В соответствии с этим признаком, ряд (7.17) сходится, если и расходится, если . Из последних неравенств определяется интервал сходимостии радиус сходимости.

Если , то при любом и ряд (7.17), а значит, и ряд (7.15) сходятся на всей числовой оси, т. е..

Если же , то при любом из числовой оси и при любом ряд расхо­дится, т. е. .

Пример 7.13. Для ряда

.

Следовательно, R = 3. Поэтому данный ряд абсолютно сходится в интервале (— 3; 3) и расходится вне отрезка [— 3; 3]. В точке получаем гармонический ряд, т. е. в этой точке заданный ряд расходится. В точкеимеем ряд, который сходится в силу теоремы Лейбница. Значит, в точке заданный ряд сходится условно.Пример 7.14. В случае ряда

Значит, R= 0.

Пример 7.15. Для ряда

Следовательно, .

Разложение функций в степенные ряды. Для приложений важно уметь данную функцию разлагать в степенной ряд, т. е. функцию представлять в виде суммы степенного ряда, так как тем самым мы получаем возможность просто вычислять значения этой функции с любой степенью точности.

Разберем частные случаи.

Рассмотрим степенной ряд

Этот ряд сходится при , причем сумма его равна .

Следовательно,

= (7.18)

и это равенство справедливо при всех х из интервала (— 1; 1).

Формула (6) называется разложением функции в степенной ряд.

Формула (6) является источником новых разложений. Разложение функции . Заменяя в разложении (7.18) на , получим

(7.19)

Считая , можно ряд (7.19) проинтегрировать по t в пределах от 0 до х. Получим:

Отсюда

(7.20)

если . Можно показать, что это разложение справедливо также при = 1.

Разложение функции . Аналогично, полагая в (6) и интегрируя полученное равенство по от 0 до х, получим разложение функции :

(7.21)

справедливое для . Можно доказать, что это разложение оста­ется верным и при х = 1, и при .

Теорема единственности.

Функция . Для этой функции производные любого порядка равны ей самой ,Отсюда ,Значит, функцияимеет следующий ряд Маклорена:

Этот ряд сходится на всей числовой оси.

Функция . Тогда ,,,и т.д. Отсюда получаем,,,и т.д. Таким образом, все производные четных порядков (в нуле) равны нулю, а нечетные производные равны 1 или –1. Поэтому функция имеет следую­щий ряд Маклорена:

Ряд (7. ) сходится при любом .

Функция . Тогда,,,и т.д. Отсюда получаем,,,и т.д. Таким образом, все производные нечетных порядков (в нуле) равны нулю, а четные производные равны 1 или –1. Поэтому функция имеет следую­щий ряд Маклорена:

Ряд (7. ) сходится при любом .

Одним из важных приложений степенных рядов является их использование в приближенных вычислениях. С помощью рядов можно, например, приближенно вычислять значения функций, определенных интегралов и т.д..

Пример 7.16

Вычислить значение с точностью до 0,0001.

Решение

По формуле (7.12) получаем:

Оценим погрешность, получаемую при отбрасывании всех членов этого ряда, начиная с пятого:

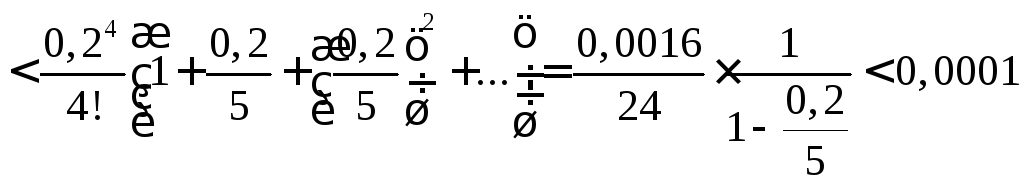
Значит, с точностью до 0,0001 имеем:

.

Пример 7.17

Вычислить интеграл 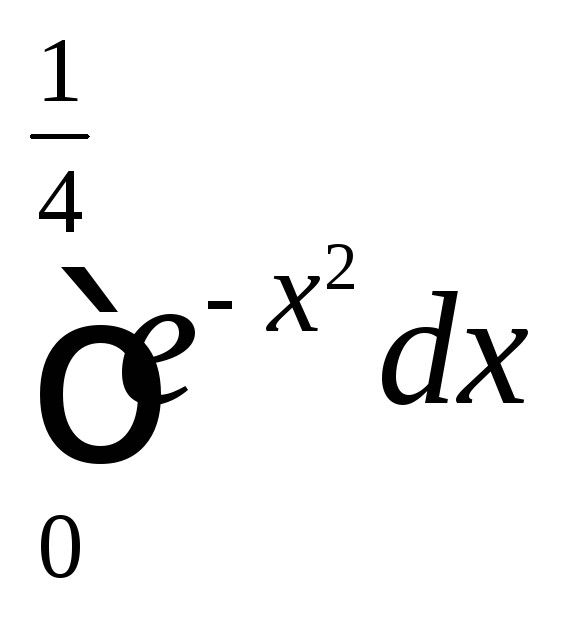с точностью до 0,0001.

В разложение () вместо подставим. Получим

Отсюда (п. 2)

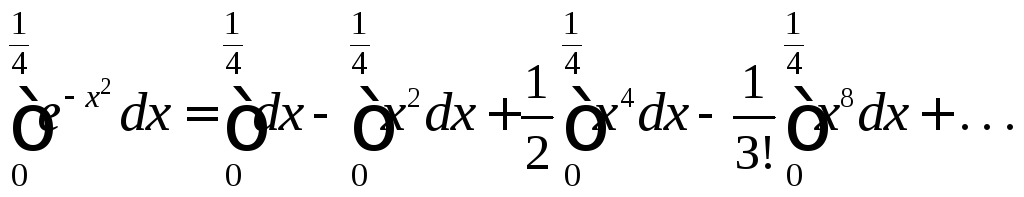
Это знакочередующийся ряд, удовлетворяющий теореме Лейбница (см. 34, п. 4). Так как то для получения нужной точности достаточно взять первые два члена ряда (15).

159