6.3. Уравнения с разделяющимися переменными.

Пусть ДУ первого порядка записано в виде (6.14). Это уравнение называется уравнением с разделяющимися переменными, если функция имеет вид

,

(6.21)

то есть представляет собой произведение функции только от переменной на функцию только от. В этом случае уравнение записывается в виде

.

(6.22)

“Разделение переменных” заключается в приведении уравнения (6.22) к виду (разделили на и умножили на)

.

(6.23)

Общее решение получается в результате интегрирования

.

(6.24)

Пример 6.1

Решить уравнение .

Решение

Перепишем, используя другое обозначение для производной,

.

Разделение переменных приводит к равенству .

В результате вычисления интегралов , получаем

, откуда .

Ответ. ; где– произвольная постоянная.

Пример 6.2

Решить уравнение .

Решение

Перепишем уравнение в виде . Разделение переменных приводит к равенству. В результате вычисления интеграловполучаем,

где - произвольная положительная постоянная.

Произвольная постоянная записана в форме для удобства записи формы общего решения.

Далее, используя свойства логарифмов, из последнего равенства получаем

.

Отсюда , где.

Отрицательные и неотрицательные решения охватываются одной формулой: ,- произвольная постоянная.

Ответ. ;- произвольная постоянная.

Если ДУ первого порядка записано в виде (6.20), то оно будет уравнением с разделяющимися переменными, если функции и можно представить в виде произведений

, ,

в которых сомножители зависят только от одной переменной. Тогда уравнение (6.20)перепишется в следующей форме:

.

(6.25)

Деля уравнение (6.24) на произведение (предполагаем, что оно не равно нулю), получаем:

.

(6.25)

Заметим, что в уравнении (6.25) множитель перед — функция только одной переменной , а множитель перед — функция только одной переменной .

Уравнение (6.25) называется уравнением с разделенными переменны­ми. Общим интегралом уравнения (6.25) является соотношение

.

(6.26)

Пример 6.3

Решить уравнение .

Решение

Интегрируя, находим . Здесь постоянная интегрирования обозначена , так как левая часть последнего ра­венства неотрицательна. Умножая последнее равенство на 2, получаем. Это уравнение семейства концентрических окружностей с центром в начале координат и радиусом .

Пример 6.4

Решить уравнение .

Решение

Разделяя переменные, получим: .

Интегрируя последнее уравнение, будем иметь: , где. Здесь произвольная постоянная записана какдля удобной записи общего решения. Используя формулу для суммы логарифмов и потенцируя последнее равенство, получим. Если считать, то это решение можно записать. Это же решение описывается равенством, в которомпроизвольная постоянная любого знака. Это семейство прямых, проходящих через начало координат.

Пример 6.5

Решить задачу Коши

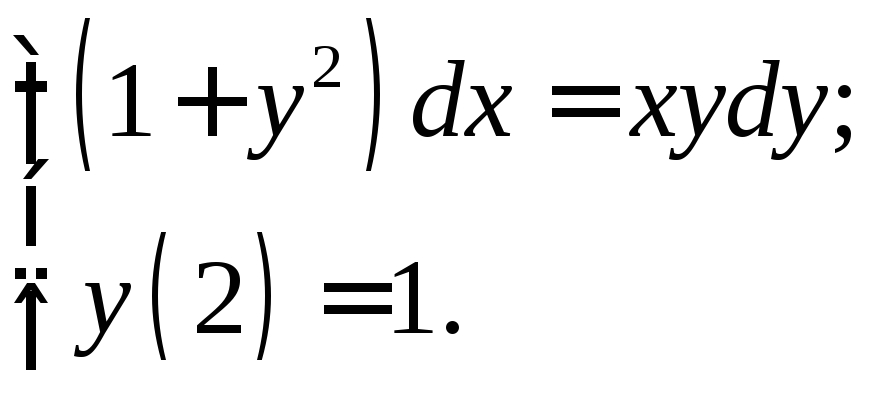
Решение

;

–общее решение уравнения.

Найдем частное решение, удовлетворяющее условию .

.

Подставим найденное значение: ,,

, – решение задачи Коши.

Пример 6.6. (Задача об охлаждении тела.)

Скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и тем­пературой воздуха. Температура воздуха равна 20° С. Известно, что в течение 20 мин тело охлаждается от 100 до 60° С. Определить закон изменения температуры в теле в зависимости от времени I.

Решение.

Согласно условию задачи имеем:

,

где k- коэффициент пропорциональности. Разделяя переменные и интегрируя, получаем

,

что после потенцирования дает

и, следовательно,

Для определения используем начальное условие: при . Отсюда:. Поэтому

.

Коэффициент пропорциональности k определяем из дополнительного условия: при. Отсюда:

или

и, следовательно,

Итак, искомая функция

.