
fiz
.pdf
Заряды на поверхностях поляризованного диэлектрика ab и cd являются связанными и принадлежат молекулам только поверхностного слоя, которых во много раз меньше по сравнению числом всех молекул диэлектрика. Заряды на этих поверхностях создадут свое электрическое поле напряженностью
E . Поскольку это внутреннее поле создано не всеми зарядами диэлектрика, а только поверхностными, его напряженность E меньше напряженности E0 внешнего электрического поля, в которое внесли диэлектрик (вспомним, что поверхностные заряды проводника образованы всеми его свободными электронами, поэтому напряженность поля E , созданного там всеми свободными зарядами, по модулю равна напряженности E0 внешнего поля).
Поскольку вектор напряженности поля E , созданного связанными зарядами на поверхностях диэлектрика, антинаправлен вектору напряженности E0 внешнего поля, то вектор напряженности E
результирующего поля будет численно равен их разности и направлен в сторону вектора E0 ,
E E0 E .
Следовательно, диэлектрик, внесенный в электрическое поле, уменьшает его напряженность.
Физический смысл : относительная диэлектрическая проницаемость показывает, во сколько раз напряженность E0 электрического поля в вакууме больше, чем напряженность E поля в диэлектрике,
|
E0 |
|
, |
|
E0 |
|
E E |
|
E |
|
|||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
108. ПОНЯТИЕ О СЕГНЕТОЭЛЕКТРИКАХ, ПЬЕЗОЭЛЕКТРИКАХ, ПИРОЭЛЕКТРИКАХ И ЭЛЕКТРЕТАХ. ПРИМЕНЕНИЕ ДИЭЛЕКТРИКОВ
У однородных и изотопных твердых аморфных диэлектриков, а также диэлектриков жидких и газообразных, в отсутствие внешнего электрического поля поляризация всегда отсутствует из-за разориентации дипольных моментов отдельных молекул. Если такой поляризованный диэлектрик удалить из внешнего электрического поля, то тепловое хаотическое движение, всегда присущее молекулам, быстро ликвидирует связанные заряды на его поверхностях и при этом суммарный дипольный момент каждой единицы объема диэлектрика станет равен нулю, т. е. поляризация исчезнет.
Однако в природе существуют кристаллические диэлектрики, молекулы которых образуют группы, обладающие самопроизвольной (спонтанной) поляризацией даже в отсутствие внешнего электрическогополя. Понятно, что эти группы могут быть образованы только из полярных молекул. Такие группы молекул называются доменами. Поведение молекул, входящих в состав домена, объясняется законами квантовой механики.
Диэлектрики, обладающие доменной структурой, называют сегнетоэлектриками. Название это происходит от слов «сегнетова соль» – наиболее типичного сегнето-электрика, который в свою очередь, был назван в честь французского аптекаря Э. Сегнетта, впервые синтезировавшего это вещество.
Все сегнетоэлектрики – кристаллы.
а) |
б) |
Рис. 108-1
Поместим кристалл неполяризованного сегнетоэлектрика (рис. 108-1, а) во внешнее электрическое поле и будем увеличивать его напряженность E0 . Под действием этого поля домены начнут все более
ориентироваться по полю (рис. 108-1, б), чему препятствует тепловое разориентирующее движение молекул.

При достижении некоторой достаточно большой напряженности все домены кристалла окажутся ориентированы по полю. Такое состояние диэлектрика называется насыщением, а соответствующая напряженность – напряженностью насыщения.
Если теперь удалить диэлектрик из электрического поля, то он сохранит поляризацию.
Способность сохранять поляризацию и в отсутствие внешнего электрического поля является самой главной особенностью, отличающей сегнетоэлектрики от остальных диэлектриков.
Чтобы теперь располяризовать сегнетоэлектрик, надо его поместить в электрическое поле, антинаправленное первоначальному.
В настоящее время известно несколько сотен сегнетоэлектриков. Второй существенной особенностью, отличающей их от остальных диэлектриков, является чрезвычайно высокое значение относительной диэлектрической проницаемости, достигающей у отдельных сегнетоэлект-риков нескольких тысяч, тогда как у остальных диэлектриков она колеблется в пределах десяти и только у воды достигает 81. И наконец, третьей особенностью сегнетоэлектриков является зависимость относительной диэлектрической проницаемости от напряженности внешнего электрического поля, тогда как у остальных диэлектриков она постоянна.
Все сегнетоэлектрики обладают этими замечательными свойствами лишь в определенном интервале температур. Например, сегнетова соль имеет доменную структуру лишь в интервале температур между -15°С и 22,5°С. При иных температурах она ведет себя как обычный диэлектрик. Эти переходные температуры, при которых диэлектрик из обычного становится сегнетоэлектриком, называются точками Кюри, по имени братьев Пьера и Жолио Кюри, которые обнаружили это явление.
Сегнетоэлектрики с высокими значениями относительной диэлектрической проницаемости применяются в качестве прокладок в конденсаторах, используемых в детекторах электромагнитных волн. У прозрачных для света сегнетоэлектриков показатель преломления зависит от величины относительной диэлектрической проницаемости, что позволяет их использовать в качестве злектрооп-тических фильтров, способных избирательно пропускать или поглощать электромагнитные волны определенного диапазона частот.
У большинства диэлектриков поляризация возникает под действием внешнего электрического поля. Однако в природе существуют диэлектрики, которые могут поляризоваться в результате механического воздействия, например, при сжатии или растяжении. Явление поляризации диэлектриков в результате механического воздействия называется прямым пьезоэлектрическим эффектом, а диэлектрики, подверженные этому эффекту, называются пъезоэлектриками. Пьезоэлектриками являются все сегнетоэлектрики, а также некоторые другие диэлектрики, например, кварц, некоторые сорта керамики.
Если пластинку, вырезанную из кристалла кварца, закрепить между двумя металлическими обкладками так, как показано на рис. 108-2, и начать сжимать, то на его ребрах возникнут связанные заряды противоположного знака. Если ее начать растягивать, то знаки поменяются на противоположные. При этом величина связанных зарядов прямо пропорциональна деформирующей силе.
Существует обратный пьезоэлектрический эффект, при котором пьезоэлектрик, внесенный в электрическое поле, деформируется: сжимается или растягивается в зависимости от направления поля относительно его осей симметрии. Если его внести в
переменное электрическое поле, частота которого близка собственной частоте колебаний пьезоэлектрического образца, то в нем возникнут механические колебания. Эти колебания будут передаваться окружающей среде, в которой начнут распространяться механические волны. Явление обратного пьезоэлектрического эффекта используется в пьезоэлектрических преобразователях, позволяющих превращать электрические сигналы в механические. Такие преобразователи используются в ультразвуковой дефектоскопии для обнаружения внутренних дефектов в непрозрачных для света деталях, в гидроакустике, акустоэлектронике и радиоэлектронике. Прямой пьезоэлектрический эффект используется также для измерения давлений, возникающих, например, в двигателях внутреннего сгорания или в стволах орудий при выстреле. О величине давления судят по показаниям прибора, измеряющего величину связанных зарядов на поверхности пьезоэлектрика.
Существует еще один способ поляризовать диэлектрик. Он состоит в изменении его температуры. Явление поляризации диэлектрика вследствие изменения его температуры называется

пироэлектрическим эффектом, а вещества, подверженные этому явлению, – пироэлектриками.
Обнаружено, что если один конец стержня, изготовленного из кристалла кварца или турмалина, нагреть, то он заряжается положительно, но при этом другой его конец в соответствии с законом сохранения зарядов приобретает отрицательный заряд. При охлаждении знаки зарядов на концах пироэлектрика соответственно меняются. При этом величина связанных зарядов на концах пироэлектрика тем больше, чем быстрее происходит процесс нагревания или охлаждения. Пироэлектрический эффект тесно связан с обратным пьезоэлектрическим эффектом. При нагревании пироэлектрика происходит механическая деформация кристалла и при этом дипольные моменты молекул диэлектрика приобретают преимущественную ориентацию, вследствие чего на его поверхностях образуются связанные заряды. Поэтому все пироэлектрики являются одновременно и пьезоэлектриками.
Пироэлектрический эффект используется в электронной промышленности при изготовлении различных высокочувствительных индикаторов и приемников электромагнитных излучений.
К диэлектрикам, способным длительное время сохранять на своей поверхности связанные электрические заряды, относятся также и многие некристаллические диэлектрики – так называемые электреты, изготовляемые искусственным путем. В электретное состояние можно перевести и некоторые кристаллические диэлектрики. Для этого диэлектрик (воск, парафин, полимеры и т. д.) с полярными молекулами расплавляют и в расплавленном состоянии помещают в сильное электростатическое поле. При этом дипольные моменты молекул диэлектрика ориентируются по полю. Затем расплав быстро охлаждают, после чего поле выключают. В затвердевшем диэлектрике молекулам трудно вернуться в исходное положение и поэтому они длительное время сохраняют свою новую ориентацию, благодаря чему на поверхности диэлектрика сохраняются связанные заряды, а в окружающем пространстве – достаточно сильное электрическое поле.
Электреты, полученные в результате расплавления диэлектрика, называют термоэлектретами. Перевести диэлектрик в электретное состояние можно и другим путем, например, воздействием радиоактивного излучения определенной частоты (радиоэлектреты), сжатием или растяжением
(механоэлектреты), трением (трибоэлектреты), световым излучением (фотоэлектреты) и другими способами.
Электреты находят очень широкое применение в современной науке и технике и прежде всего в качестве постоянных источников электрических полей (в микрофонах и телефонах, виброизмерительных приборах, генераторах электрических сигналов, электрометрах и т. д.). Они широко используются в качестве различных датчиков в дозиметрии, позволяя обнаруживать источники радиоактивных излучений и измерять их интенсивность. Их используют для изготовления чувствительных гигрометров, барометров и манометров. Фотоэлектреты используются для получения моментальных снимков в электрографии.
109. ЭЛЕКТРОЕМКОСТЬ ПРОВОДНИКА. ЭЛЕКТРОЕМКОСТЬ ПРОВОДЯЩЕЙ СФЕРЫ
Сообщим уединенному проводнику некоторый заряд. При этом он распределится по поверхности проводника так, что все потенциалы точек поверхности станут одинаковы. Если теперь этому проводнику сообщить еще такой же заряд, т. е. удвоить заряд проводника, то он точно так же распределится по поверхности проводника и при этом потенциал проводника тоже удвоится. Если мы изменим заряд проводника в несколько раз, то и его потенциал изменится во столько же раз. Но при этом величина, равная отношению заряда, сообщенного проводнику, к потенциалу, который он при этом приобретает, будет оставаться постоянной для данного проводника. Эта величина характеризует способность проводника накапливать заряды и называется электроемкостью проводника (или просто емкостью).
Емкость проводника равна отношению заряда q , сообщенного проводнику, к потенциалу , который при этом приобрел:
C |
q |
|
(109.1) |
|
|||
|
|
|
|
Физический смысл емкости проводника: емкость проводника равна заряду, который надо сообщить проводнику, чтобы его потенциал изменился на единицу.

Емкость – скалярная положительная величина. Единица емкости в СИ – фарад (Ф). Физический смысл фарада: 1 Ф – емкость проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл.
Другие единицы емкости: пикофарад (пФ), нанофарад (нФ), микрофарад (мкФ), миллифарад (мФ). 1 пФ = 10-12 Ф, 1 нФ = 10-9 Ф, 1 мкФ = 10-6 Ф, 1 мФ = 10-3 Ф.
Название «емкость» эта величина получила потому, что в свое время электричество считали некоей жидкостью, способной переливаться из одного заряженного тела в другое. Чем больше «жидкости» надо было влить в проводник, чтобы изменить его потенциал на единицу, тем больше емкость такого проводника. Известно, что емкость сосуда для жидкости не зависит от материала, из которого изготовлен сосуд. Емкость стеклянного трехлитрового баллона равна емкости трехлитрового бидона из алюминия. Точно так же и емкость проводника не зависит от вещества. Емкость шара из алюминия равна емкости шара такого же радиуса из меди.
Емкость проводника зависит от его размеров, формы , наличия поблизости других проводников, а
также от диэлектрических свойств среды, окружающей данный проводник. |
|
|
|
|
С увеличением объема проводника его емкость увеличивается. |
|
|
|
Если к незаряженному проводнику 1 приблизить |
заряженный |
проводник 2 |
|
(рис. 109-1), то свободные электроны проводника 1 |
сместятся так, |
что на его |
Рис. 109-1 |
ближайшей к проводнику 2 части поверхности возникнет заряд противоположного |
||
знака (отрицательный). Это явление называется электростатической индукцией или заряжением через влияние. Индуцированные отрицательные заряды проводника 1 создадут на проводнике 2 свой потенциал, противоположный по знаку относительно собственного потенциала проводника 2. В результате, потенциал 2 проводника понизится. Но при этом его заряд не изменится, значит, соответственно формуле (109.1) емкость проводника 2 при поднесении к нему проводника 1 увеличится.
Приближение к проводнику другого проводника увеличивает их емкость.
|
Поместим положительно заряженный проводник 1 в диэлектрик (рис. 109-2). |
|
При этом диэлектрик поляризуется. Заряды в его молекулах сместятся так, что |
|
ближайшими к поверхности проводника окажутся заряды противоположного знака, |
|
т. е. отрицательные. Они понизят потенциал проводника, а поскольку его заряд при |
|
этом не изменится, то согласно формуле (109.1) емкость проводника увеличится. |
|
Помещение проводника в диэлектрик увеличивает его емкость. Емкость |
Рис. 109-2 |
проводника прямо пропорциональна относительной диэлектрической проницаемости |
среды, в которой он находится.
Подчеркнем, что емкость проводника не зависит ни от зарядов на проводнике, ни от его потенциала. Емкость проводника не изменится, если его зарядить или разрядить. Емкость проводника не зависит от его агрегатного состояния. Капля ртути имеет такую же емкость, как и стальной шарик такого же радиуса.
Выведем формулу емкости уединенного проводника сферической формы с радиусом R , расположенного в среде с диэлектрической проницаемостью . Если проводнику сообщен заряд q , то
потенциал проводника равен: |
|
|
|
q |
|
|
. |
|
4 R |
||
|
0 |
|
Подставим в знаменатель формулы емкости (109.1) вместо потенциала правую часть этого
выражения. Получим:
c q q 4 0 R ,q
C 4 0 R
Емкость уединенного проводника сферической формы прямо пропорциональна относительной диэлектрической проницаемости среды, окружающей проводник, и радиусу проводника.

110. КОНДЕНСАТОРЫ. ЕМКОСТЬ КОНДЕНСАТОРА. ЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
Электрическое поле уединенного проводника рассеяно в окружающем пространстве, вследствие чего энергия такого поля в единице объема пространства невелика. Между тем на практике иногда возникает необходимость сосредоточить в некотором пространстве достаточный запас электрической энергии, чтобы потом в нужный момент ее использовать. Для этого необходимо увеличить емкость проводника.
Чтобы увеличить емкость проводника, не увеличивая его размеров, достаточно приблизить к нему другой проводник, не касаясь первого. При этом мы получим устройство, которое называется конденсатором.
Конденсатор – это система двух близко расположенных друг к другу проводников. Проводники, образующие конденсатор, называются его обкладками.
Если обкладки конденсатора зарядить разноименно (для этого достаточно сообщить заряд одной из обкладок, при этом на второй обкладке вследствие электростатической индукции возникнет заряд противоположного знака), то между ними возникнет электрическое поле, которое почти целиком будет сосредоточено между обкладками и почти не будет рассеиваться в окружающем пространстве.
Простейшим по устройству и наиболее распространенным является плоский конденсатор, представляющий собой две плоские проводящие пластины, разделенные слоем диэлектрика. При условии, что расстояние между обкладками плоского конденсатора значительно меньше корня квадратного из площади обкладок, электрическое поле между обкладками будет однородным и будет практически целиком сосредоточено между ними, тогда как за обкладками поле будет отсутствовать. Однородность поля будет нарушаться только вблизи краев обкладок.
Каждый конденсатор характеризуется его емкостью и максимальным напряжением на обкладках, при котором диэлектрик еще не теряет своих изолирующих свойств. При превышении максимального напряжения (напряжения пробоя) диэлектрик будет пробит и конденсатор испортится. Емкость
конденсатора и его пробивное напряжение обычно написаны на нем. |
|
|||||||||
Емкость конденсатора C равна отношению |
|
заряда |
q на одной |
из его обкладок к разности |
||||||
потенциалов 1 2 U между ними: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
q |
|
|
|
C |
q |
|
|
(110.1) |
|
|
|
|
U |
|
|||||
|
|
|
|
|
|
|
|
|||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Физический смысл емкости конденсатора: емкость конденсатора равна заряду, который надо ему сообщить, чтобы изменить разность потенциалов между его обкладками на единицу.
Емкость конденсатора не зависит ни от заряда на его обкладках, ни от разности потенциалов между ними. Незаряженный конденсатор имеет точно такую же емкость, как и в случае его зарядки. Конденсаторы, продающиеся в магазинах радиотоваров, конечно, не заряжены, однако их емкость указана на них. Емкость конденсатора не зависит также от металла, из которого изготовлены его обкладки, и от наличия вблизи других конденсаторов.
Емкость конденсатора зависит от его формы, размеров и диэлектрика, помещенного между обкладками. Наличие диэлектрика между обкладками увеличивает емкость конденсатора.
Выведем формулу емкости плоского конденсатора. Его емкость C , как и емкость любого другого конденсатора, определяется формулой (110.1),
C Uq
Здесь q – заряд на обкладке конденсатора, U – напряжение между обкладками.
Поскольку поле между обкладками плоского конденсатора однородное, то напряжение U связано с его напряженностью E формулой
E |
U |
, откуда |
U Ed . |
|
d |
||||
|
|
|
Напряженность однородного тела электрического поля между двумя плоскими поверхностями с одинаковой поверхностной плотностью зарядов равна:

|
|
|
|
|
|
E |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Здесь – относительная |
диэлектрическая |
|
проницаемость диэлектрика между обкладками |
||||||||||
конденсатора, ст -поверхностная плотность зарядов на его обкладках. |
|||||||||||||
Подставим это выражение в предыдущую формулу: |
|
|
|
||||||||||
|
|
|
|
|
U |
d , |
где |
|
q |
. |
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Тогда C |
q 0 |
или C |
q |
0 S |
, |
|
|
|
|
|
|
|
|
d |
qd |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
C |
|
0 S |
(110.2) |
||||
|
|
|
|
|
|
|
|
d |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь S – площадь обкладок конденсатора (точнее, площадь одной обкладки), d – расстояние между обкладками.
Емкость плоского конденсатора прямо пропорциональна относительной диэлектрической проницаемости диэлектрика между обкладками, площади обкладок конденсатора и обратно пропорциональна расстоянию между обкладками.
Из формулы (110.2) следует, что
|
|
|
Cd |
, |
|
|
0 |
|
|
|
|||
|
|
S |
|
|||
|
|
|
|
|||
поэтому единицей электрической постоянной, кроме |
|
Кл2 |
, является также Ф м м2 Ф м . |
|||
|
Н м2 |
|||||
|
|
|
|
|
||
На рис. 110-1 показано условное изображение конденсатора постоянной емкости (слева) и переменной емкости (справа) на схемах. Вращая ручку конденсатора переменной емкости, мы меняем площадь перекрывающейся части обкладок и расстояние между ними и тем самым изменяем нужным образом емкость конденсатора.
Если обкладки плоского конденсатора сдвинуты относительно друг друга (рис. 110-2), то в формуле (110.2) S – это площадь перекрываемой части обкладок.
Конденсаторы могут иметь различную форму. Бывают плоские, сферические, цилиндрические конденсаторы, а также конденсаторы более сложной формы (желудевые, пальчиковые и др.). По роду диэлектрика, помещенного между обкладками, конденсаторы бывают слюдяные, бумажные (диэлектрик – парафинированная бумага), воздушные, керамические и др.
В бумажном конденсаторе диэлектриком служит парафинированная бумага, а обкладками – полосы металлической фольги, между которыми она располагается. Их вместе сворачивают в небольшой рулон, который помещают в специальный корпус, имеющий два вывода для включения в цепь.
Существуют электролитические конденсаторы, в которых диэлектриком является пленка из оксида алюминия, погруженная в электролит. Эта пленка служит изолятором при определенном направлении электрического поля между обкладками, а если это направление изменить на противоположное, то она станет пропускать ток, начнет нагреваться и разрушаться. Поэтому при включении электролитического конденсатора в цепь надо следить за соблюдением полярности, т. е. ту обкладку, которая обозначена знаком «+», подключать к плюсу источника зарядов, а «–» – к минусу, и ни в коем случае наоборот, иначе произойдет пробой диэлектрика. Если же на корпусе конденсатора полярность выводов не обозначена, то их можно подключать к источнику зарядов произвольно.
Конденсаторы находят широкое применение во всех радиотехнических устройствах.
111. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ
Для получения нужной емкости конденсаторы соединяют последовательно или параллельно в батарею конденсаторов.

Последовательное соединение конденсаторов
Если конденсаторы соединить так, чтобы одна обкладка предыдущего конденсатора была соединена только с одной обкладкой последующего конденсатора, то такое соединение будет называться
последовательным (рис. 111-1),
При зарядке такой батареи конденса торов все обкладки, разделенные диэлектриком, окажутся заряженными разноименно.
Рис. 111-1 |
Сообщим левой обкладке конденсатора с емкостью C1 |
заряд q , соединив ее с |
|
клеммой, потенциал которой 1 (рис, 111-2). При этом потенциал этой обкладки тоже станет равен 1 . Вследствие явления электростатической индукции на правой обкладке конденсатора C1 возникнет такой же по величине, но противоположный по знаку заряд q . Правая обкладка конденсатора C1 соединена с левой обкладкой конденсатора C2 . Так как до зарядки суммарный заряд этих обкладок был равен нулю,
то по закону сохранения зарядов он должен остаться равным нулю и после зарядки. Если правая обкладка конденсатора C1 приобрела заряд q , значит, левая обкладка конденсатора C2 приобретает
при этом равный по модулю, но положительный заряд q , – только тогда суммарный заряд этих
обкладок останется равным нулю. Это правило относится и к остальным последовательно соединенным конденсаторам батареи.
П р а в и л о 1 : Модули зарядов на обкладках последовательно соединенных конденсаторов одинаковы,
q1 q2 q3 ... qN q
Здесь N – число конденсаторов в батарее.
Обратимся опять к рис. 111-2. Обозначим потенциал правой обкладки конденсатора C1 буквой a . Поскольку правая обкладка конденсатора C1
соединена с левой обкладкой конденсатора C2 проводником, значит, потенциал левой обкладки конденсатора C2 тоже будет равен a (напомним, что если
проводники соединить, то их потенциалы станут одинаковы). Обозначим потенциал правой обкладки конденсатора C2 буквой b . Тогда и потенциал левой обкладки
конденсатора C3 , соединенной с правой обкладкой конденсатора C2 , тоже будет b . И наконец, потенциал правой обкладки конденсатора C3 , соединенной с клеммой, потенциал которой равен 2 , тоже будет 2 . Тогда разность потенциалов 1 2 на клеммах этой батареи будет равна
1 2 1 a a b b 2 ,
где 1 2 Uобщ , 1 a U1 , a |
b U2 , b 2 U3 . |
|
|
|
Следовательно, Uобщ U1 U2 |
U3 . |
|
|
|
Для батареи, состоящей из N последовательно соединенных конденсаторов, последнее равенство |
||||
примет вид: |
|
|
|
|
|
|
|
N |
|
|
|
Uобщ U1 U2 U3 ... UN |
Ui |
(111.1) |
|
|
|
i 1 |
|
Здесь i – порядковый номер конденсатора от 1-го до N-го.
П р а в и л о 2 : общее напряжение (разность потенциалов) на батарее последовательно соединенных конденсаторов равно сумме напряжений (разностей потенциалов) на каждом конденсаторе.
Из формулы (111.1) следует, что U |
|
|
q |
, U |
|
|
q |
, U |
|
|
q |
, U |
|
|
q |
, …, U |
|
|
q |
. |
общ |
Cобщ |
1 |
|
2 |
|
3 |
|
N |
|
|||||||||||
|
|
|
|
C1 |
|
C2 |
|
C3 |
|
|
CN |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Подставив эти выражения в формулу (111.1), получим:
q q q q ... q .
Cобщ C1 C2 C3 CN
Сократив заряд q , получим формулу, определяющую общую емкость батареи:
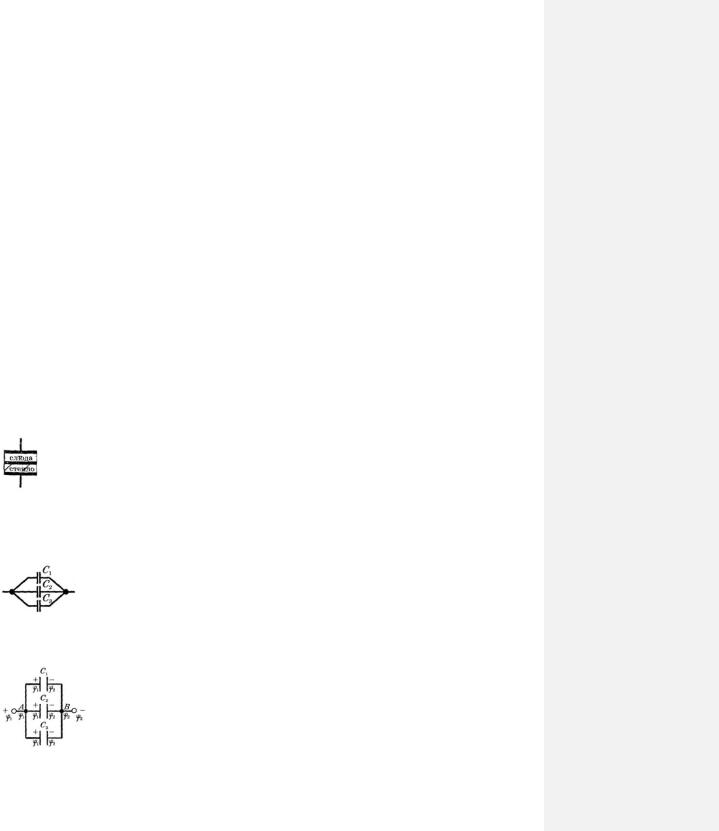
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
... |
1 |
|
|
|
|
|
|
|
|
|
(111.2) |
||||||||||||||||
|
|
|
C |
|
C |
C |
2 |
|
C |
C |
N |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
общ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
П р а в и л о |
3 : величина, обратная общей емкости последовательно соединенных конденсаторов, |
||||||||||||||||||||||||||||||||||||||||||
равна сумме величин, обратных емкостям отдельных конденсаторов. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Если имеется 2 конденсатора, то |
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
C1 C2 |
, откуда |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Cобщ |
|
C1 |
C2 |
|
|
|
|
|
|
|
|
C1C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Cобщ |
|
|
|
C1C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(111.3) |
||||||||||||||
|
|
|
|
|
|
|
C1 C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Если все |
N последовательно |
соединенных |
|
конденсаторов |
имеют |
одинаковую емкость C , то |
|||||||||||||||||||||||||||||||||||||
формула (111.1) примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uобщ U U U ... U |
|
или |
|
Uобщ NU |
, |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
а формула (111.2) в этом случае будет выглядеть так: |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
... |
1 |
N |
1 |
, откуда |
||||||||||||||||||||||||
|
|
Cобщ |
C |
|
C |
C |
C |
C |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(111.4) |
||||||
|
|
|
|
|
|
|
|
общ |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Общая емкость N одинаковых, последовательно соединенных конденсаторов, в N раз меньше емкости каждого конденсатора.
Подставив в формулу (111.3) любые численные значения емкостей отдельных конденсаторов, от самых больших, до самых малых, и вычислив их общую емкость, можно убедиться в справедливости следующего правила: общая емкость последовательно соединенных конденсаторов меньше емкости любого из них.
Например, если емкость одного из последовательно соединенных конденсаторов 1000 пФ, а второго 0,001 пФ, то общая емкость будет меньше 0,001 пФ. В этом легко убедиться, подставив эти числа в формулу (111.3) и вычислив Cобщ . Следовательно, чтобы уменьшить емкость батареи конденсаторов, их
нужно соединить последовательно.
Если между обкладками конденсатора поместить разные диэлектрики так, как показано на рис. 111-3, то получим последовательно соединенные конденсаторы с одинаковыми площадями обкладок. Число конденсаторов будет равно числу диэлектриков, а расстояние Рис. 111-3 между обкладками будет равно толщине диэлектриков. Поверхности диэлектриков, параллельные обкладкам конденсатора, сами станут обкладками, поскольку на них возникнут
связанные заряды противоположного знака.
Параллельное соединение конденсаторов
Если конденсаторы соединить так, чтобы их левые обкладки оказались соединенными в одной точке, а правые – в другой (рис. 111-4), то такое соединение будет называется параллельным. Если одни соединенные друг с другом обкладки подключить к положительной клемме источника зарядов, то все эти обкладки тоже
Рис. 111-4 окажутся заряженными положительно и будут иметь одинаковый потенциал, например, 1 (рис. 111-5). При этом все другие обкладки, тоже соединенные друг с
другом, окажутся заряженными отрицательно и будут иметь одинаковый потенциал 1 .
Таким образом, на обкладках всех параллельно соединенных конденсаторов окажется одинаковая разность потенциалов 1 2 , т. е. на них будет одинаковое
напряжение U ,
|
|
|
|
U1 U2 |
U3 ... UN U |
|
|
|
Здесь U1 , |
U 2 , |
U 3 , …, U N – напряжения на отдельных конденсаторах, N – число |
||||
Рис. 111-5 |
конденсаторов в батарее. |
|
|
||||
П р а в и л о |
1 |
: напряжения на |
параллельно соединенных конденсаторах |
||||
|
|||||||

одинаковы.
Пусть батарее конденсаторов, соединенных параллельно, сообщили заряд qобщ . Если емкости
конденсаторов различны, то при одинаковых напряжениях на них согласно формуле емкости конденсатора заряды конденсаторов q1 , q2 , q3 , …, qN тоже будут разными. По закону сохранения
зарядов общий заряд батареи должен быть равен их сумме:
|
N |
|
qобщ q1 q2 q3 ... qN |
qi |
(111.5) |
|
i 1 |
|
П р а в и л о 2 : общий заряд батареи параллельно соединенных конденсаторов равен сумме зарядов на каждом из них.
Поскольку согласно формуле емкости qобщ CобщU , q1 C1U , q2 C2U , q3 C3U , …, qN CNU , то подставив правые части этих выражений в формулу (111.4), получим:
CобщU C1U C2U C3U ... CNU .
Сократив U , получим формулу, определяющую общую емкость батареи параллельно соединенных конденсаторов:
|
|
|
|
|
N |
|
|
|
|
|
|
Cобщ C1 C2 C3 ... CN Ci |
|
|
|
|
|||
|
|
|
|
|
i 1 |
|
|
|
|
П р а в и л о |
3 : общая емкость батареи параллельно |
соединенных конденсаторов |
равна сумме |
||||||
емкостей отдельных конденсаторов. |
|
|
|
|
|
|
|
||
Если все N |
конденсаторов, соединенных параллельно, |
имеют одинаковую емкость C , то согласно |
|||||||
формуле (111.4) их общие заряд и емкость будут равны: |
|
|
|
|
|
|
|
||
|
qобщ q q q ... q |
или |
|
qобщ Nq |
|
|
|
||
где q – заряд каждого конденсатора, |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
Cобщ C C C ... C |
или |
|
Cобщ NC |
|
|
|||
|
|
|
|
||||||
Емкость батареи, состоящей из N параллельно соединенных конденсаторов, в N |
раз больше |
||||||||
емкости каждого из них. Следовательно, чтобы увеличить емкость батареи, конденсаторы нужно соединять параллельно.
Если между обкладками конденсатора поместить разные диэлектрики так, как показано на рис. 111-6, то получим параллельно соединенные конденсаторы, поскольку разность потенциалов на их обкладках будет одинакова. Число конденсаторов будет равно числу диэлектриков, расстояние между обкладками будет равно толщине диэлектриков
(если она у них одинакова), а площадь обкладок каждого конденсатора будет равна площади поверхности каждого диэлектрика, параллельной обкладкам.
Если у конденсатора изменить расстояние между его обкладками или поменять диэлектрик, не отключая конденсатор от источника, то при этом будут изменяться емкость конденсатора и заряд на его обкладках, а напряжение на них изменяться не будет, поскольку будет оставаться равным напряжению на клеммах источника.
Если конденсатор отключить от источника зарядов, а затем изменить расстояние между его обкладками или поменять диэлектрик, то при этом будут изменяться емкость конденсатора и напряжение на обкладках, а заряд будет сохраняться.
112. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ОБЪЕМНАЯ ПЛОТНОСТЬ ЭНЕРГИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Электрическое поле, как и всякое силовое поле, обладает энергией, которая может превращаться в другие виды энергии. Если обкладки заряженного конденсатора, между которыми создано электрическое поле, соединить проводником, то между обкладкой и поднесенным к ней концом проводника может проскочить искра. При этом конденсатор может разрядиться, а энергия его поля – превратиться в другие виды энергии: тепловую, световую, механическую (будет слышен характерный треск).
По проводнику, соединившему обкладки, в момент соединения пройдет ток. При этом будет совершена работа перемещения зарядов по проводнику, причем совершена она будет за счет энергии
электрического поля конденсатора. Поскольку конденсатор полностью разрядится, работа перемещения зарядов A будет равна всей электрической энергии поля конденсатора Wэл :
A Wэл .
Если этот конденсатор плоский, то поле, создаваемой каждой обкладкой, однородно. Работа перемещения заряда q в однородном электростатическом поле напряженностью E1 вдоль силовой линии
на расстояние d равна
A E1qd .
Здесь E1 – напряженность поля, созданного каждой обкладкой, d – расстояние между ними, равное
длине проводника, соединившего обкладки.
Поскольку обкладок две, то напряженность E поля между обкладками вдвое больше E1 :
E 2E , откуда |
E |
E |
. |
|
|||
1 |
1 |
2 |
|
|
|
|
Тогда W |
Eqd |
. |
|
||
эл |
2 |
|
|
|
Напряженность однородного электрического поля плоского конденсатора связана с напряжением на его обкладках соотношением
|
|
E |
U |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
d |
|
|
|
||||||
С учетом этого W |
Uqd |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
эл |
2d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Wэл |
|
Uq |
|
|
|
|
|
(112.1) |
||||
|
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|||||
Поскольку из определения емкости плоского конденсатора следует, что q CU |
и U |
q |
, то |
|||||||||||
C |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
W |
CU 2 |
|
|
|
(112.2) |
|||||||
|
|
|
|
|
|
|||||||||
|
|
эл |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
q2 |
|
|
|
(112.3) |
||||||
|
|
|
|
|
||||||||||
|
|
эл |
|
|
|
2C |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Формулы (112.1), (112.2) и (112.3) определяют энергию электрического поля. В них энергия выражена через величины заряда q , напряжения U и емкости C , которые в свою очередь определяются
свойствами заряженных тел, создающих поле (их размерами, формой и др).
Но электрическое поле может существовать независимо от его источников и распространяться в пространстве, перенося при этом энергию. Поэтому важно выразить величину этой энергии через
величину, характеризующую само поле, т. е. через его напряженность E . Поскольку, когда поле распространяется в пространстве, оно не имеет четко очерченных границ, внутри которых сосредоточена его энергия, то для характеристики энергетических свойств электрического поля английским физиком Максвеллом было введено понятие объемной плотности энергии wэл .
Объемная плотность энергии электрического поля wэл равна отношению энергии электрического поля в некотором объеме пространства, к величине этого объема V ,
wэл |
Wэл |
(112.4) |
|
V |
|||
|
|
Физический смысл объемной плотности энергии электрического поля: объемная плотность энергии электрического поля равна энергии этого поля в еденице объема пространства, занятого им.
Объемная плотность энергии электрического поля – скалярная положительная величина.
Еденица объемной плотности энергии электрического поля в СИ – джоуль на метр в кубе (Дж/м3).
