
- •Передмова
- •МЕХАНІКА
- •1. КІНЕМАТИКА МАТЕРІАЛЬНОЇ ТОЧКИ
- •1.1. Основні поняття
- •1.4. Прямолінійний рух
- •1.5. Криволінійний рух. Рівномірний рух по колу
- •2. ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
- •2.1. Основні закони динаміки. Сила. Рівнодійна сила
- •2.2. Сили в механіці
- •2.4. Алгоритм розв’язання кількісних задач із фізики
- •2.5. Методичні рекомендації щодо розв’язання задач з динаміки
- •2.6. Приклади розв’язання задач
- •3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ
- •3.1. Імпульс тіла. Імпульс сили
- •3.2. Закон збереження імпульсу
- •3.3. Реактивний рух
- •3.4. Енергія. Закон збереження енергії. Види енергії
- •3.5. Види механічної енергії та їх зв’язок з роботою
- •3.6. Механічна робота і потужність
- •3.7. Механічний удар
- •3.8. Прості механізми
- •4. МЕХАНІКА ТВЕРДОГО ТІЛА
- •4.1. Основні поняття
- •4.2. Умови і види рівноваги твердого тіла
- •4.3. Момент імпульсу. Закон збереження моменту імпульсу
- •4.4. Зіставлення рівнянь механіки поступального й обертального рухів (табл. 2)
- •4.5. Приклади розв’язання задач
- •5. ГІДРОСТАТИКА І АЕРОСТАТИКА
- •5.1. Тиск
- •5.2. Закон Паскаля
- •5.3. Гідростатичний тиск
- •5.4. Сполучені посудини
- •5.5. Гідростатичний парадокс
- •5.6. Гідравлічна машина
- •5.7. Закон Архімеда
- •5.8. Умови плавання тіл (табл. 3)
- •5.9. Атмосферний тиск, його вимірювання
- •5.10. Приклади розв’язання задач
- •6. ГІДРОДИНАМІКА І АЕРОДИНАМІКА
- •6.1. Струминна течія рідин і газів
- •6.2. Рівняння Бернуллі
- •6.3. Підйомна сила крила літака
- •6.4. Коефіцієнт лобового опору для тіл різної форми (табл. 4)
- •1. ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ БУДОВИ РЕЧОВИНИ
- •1.1. Основні положення молекулярно-кінетичної теорії та їх дослідне обґрунтування
- •2. ВЛАСТИВОСТІ ГАЗІВ (ГАЗОВІ ЗАКОНИ)
- •2.2. Газові закони
- •2.3. Закон Дальтона
- •2.5. Середня довжина вільного пробігу молекул
- •2.6. Приклади розв’язання задач
- •3. ВЛАСТИВОСТІ ПАРИ
- •3.1. Пара. Випаровування і конденсація
- •3.2. Насичена і ненасичена пара
- •3.3. Вологість повітря (відносна й абсолютна). Точка роси
- •3.4. Кипіння. Перегріта рідина
- •3.5. Приклади розв’язання задач
- •4.2. Поверхнева енергія. Поверхневий натяг
- •4.3. Явище змочування. Капілярні явища
- •4.4. Формула Лапласа
- •4.5. Приклади розв’язання задач
- •5. ВЛАСТИВОСТІ ТВЕРДИХ ТІЛ
- •5.1. Кристалічні та аморфні тіла. Їхні властивості
- •5.2. Типи твердих кристалів
- •5.3. Рідкі кристали
- •5.4. Дефекти кристалічних ґраток
- •5.5. Механічні властивості твердих тіл
- •5.6. Приклади розв’язання задач
- •6. ТЕПЛОВЕ РОЗШИРЕННЯ ТВЕРДИХ І РІДКИХ ТІЛ
- •6.1. Графік залежності потенціальної енергії взаємодії найпростіших молекул від відстані між ними (потенціальна яма)
- •6.2. Лінійне й об’ємне розширення твердих і рідких тіл
- •6.3. Особливості теплового розширення води
- •6.4. Приклади розв’язання задач
- •1.1. Внутрішня енергія ідеального газу
- •1.2. Робота ідеального газу. Її геометричне тлумачення
- •1.5. Питома теплоємність речовини
- •1.6. Питома теплота згоряння палива. ККД нагрівача
- •1.7. Змінювання агрегатного стану речовини
- •2. ПЕРШИЙ ЗАКОН ТЕРМОДИНАМІКИ. АДІАБАТИЧНИЙ ПРОЦЕС
- •3. ДРУГИЙ ЗАКОН ТЕРМОДИНАМІКИ. ЕНТРОПІЯ
- •4. ТЕПЛОВІ ДВИГУНИ
- •ЕЛЕКТРОДИНАМІКА
- •1. ЕЛЕКТРОСТАТИКА
- •1.1. Електричний заряд. Закон збереження заряду
- •1.7. Електризація тіл
- •2. ПОСТІЙНИЙ СТРУМ
- •2.1. Електричний струм. Сила струму. Густина струму
- •2.3. Послідовне і паралельне з’єднання провідників
- •2.4. ЕРС. Закон Ома для повного кола. З’єднання елементів
- •2.6. Приклади розв’язання задач
- •3. СТРУМИ ПРОВІДНОСТІ
- •3.2. Струм в електролітах
- •3.4. Струм у напівпровідниках
- •3.5. Струм у вакуумі (струм переносу)
- •3.6. Приклади розв’язання задач
- •4. МАГНЕТИЗМ
- •4.1. Магнітне поле. Магнітна індукція поля
- •4.2. Магнітне поле струму
- •4.3. Дія магнітного поля на рухомий заряд (сила Лоренца) і провідник зі струмом (сила Ампера). Правило лівої руки
- •4.4. Дія магнітного поля на рамку зі струмом. Магнітний потік
- •4.5. Закон взаємодії паралельних струмів
- •4.6. Магнітне поле у речовині
- •4.7. Приклади розв’язання задач
- •5. ЕЛЕКТРОМАГНІТНА ІНДУКЦІЯ
- •5.1. Явище електромагнітної індукції. Вихрове електричне поле
- •5.3. Індукційні струми в суцільних провідниках
- •5.4. Самоіндукція. Індуктивність. Енергія магнітного поля
- •5.5. Електромагнітне поле. Теорія Максвелла в якісному вигляді
- •5.6. Приклади розв’язання задач
- •ФІЗИКА КОЛИВАНЬ
- •1. КОЛИВАЛЬНИЙ РУХ
- •1.1. Основні поняття
- •1.2. Гармонічні коливання
- •2. ЗМІННИЙ СТРУМ
- •2.1. Одержання змінного синусоїдного струму. Закономірності змінного струму
- •2.2. Діюче значення змінного струму
- •2.3. Опір змінному струму. Закон Ома для змінного струму
- •2.4. Електричний резонанс. Резонанс напруг. Резонанс струмів
- •2.5. Випрямлення змінного струму
- •2.6. Трансформація змінного струму
- •2.7. Змінний струм високої частоти
- •2.8. Приклади розв’язання задач
- •3. ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ
- •3.2. Закономірності вільних електромагнітних коливань. Згасаючі коливання
- •3.3. Отримання незгасаючих електромагнітних коливань
- •3.4. Приклади розв’язання задач
- •4. МЕХАНІЧНІ ХВИЛІ. ЗВУК
- •4.1. Поздовжні і поперечні хвилі. Промінь. Довжина хвилі. Фронт хвилі
- •4.2. Принцип Гюйгенса
- •4.3. Інтерференція хвиль
- •4.4. Дифракція хвиль
- •4.5. Звук. Звукові хвилі. Інтенсивність, висота і тембр звуку
- •4.6. Луна. Звуковий резонанс
- •4.7. Приклади розв’язання задач
- •5. ЕЛЕКТРОМАГНІТНІ ХВИЛІ
- •5.1. Випромінювання електромагнітних хвиль відкритим коливальним контуром
- •5.3. Принцип радіозв’язку. Модуляція і детектування (демодуляція)
- •5.4. Класифікація радіохвиль і особливості їх поширення
- •5.5. Приклади розв’язання задач
- •ОПТИКА
- •1. ХВИЛЬОВА ОПТИКА
- •1.1. Монохроматичне світло. Заломлення світла
- •1.2. Дисперсія світла
- •1.4. Інтерференція білого світла за Френелем
- •1.5. Інтерференція білого світла за Ньютоном. Кільця Ньютона
- •1.6. Дифракція білого світла
- •1.7. Поляризація світла
- •2. ГЕОМЕТРИЧНА ОПТИКА
- •2.2. Закони відбивання світла
- •2.3. Закони заломлення світла. Повне відбивання світла
- •2.4. Хід променів через плоскопаралельну пластинку, призму
- •2.5. Сферичні лінзи
- •2.6. Око як оптична система
- •2.8. Сферичні дзеркала
- •2.9. Приклади розв’язання задач
- •3. ВИПРОМІНЮВАННЯ ТА СПЕКТРИ
- •3.1. Люмінесценція
- •3.2. Інфрачервоні та ультрафіолетові промені
- •3.3. Рентгенівські промені
- •3.4. Спектри випромінювання. Спектри поглинання
- •3.5. Спектральний аналіз
- •1.1. Поняття про простір і час
- •1.2. Постулати СТВ. Перетворення Лоренца
- •1.4. Приклади розв’язання задач
- •2. КВАНТОВА ОПТИКА
- •2.1. Теорія Планка. Імпульс фотона
- •2.2. Фотоефект
- •2.3. Фотоелементи та їх застосування
- •2.4. Світловий тиск
- •2.5. Корпускулярно-хвильовий дуалізм
- •2.6. Хімічний вплив світла. Чорно-біла фотографія. Фотосинтез. Ланцюгові реакції
- •2.7. Приклади розв’язання задач
- •3. ФІЗИКА АТОМА
- •3.1. Планетарна модель атома Резерфорда
- •3.2. Постулати Бора. Борівські орбіти
- •3.3. Атом Гідрогену за Н. Бором
- •3.4. Приклади розв’язання задач
- •4. ФІЗИКА АТОМНОГО ЯДРА
- •4.1. Відкриття протона і нейтрона
- •4.2. Теорія будови ядра
- •4.3. Енергія зв’язку ядра. Дефект маси
- •4.4. Природна радіоактивність
- •4.6. Часткове звільнення внутрішньоядерної енергії при екзотермічних ядерних реакціях
- •4.7. Закон радіоактивного розпаду
- •4.8. Приклади розв’язання задач
- •5. ЕЛЕМЕНТАРНІ ЧАСТИНКИ
- •5.1. Фізика елементарних частинок
- •5.2. Приклади розв’язання задач
- •Предметний покажчик

Електродинаміка
1.Електростатика
1.1.Електричний заряд. Закон збереження заряду
Електричний заряд (q) — фізична величина, яка харак-
теризує властивість тіл і частинок вступати в електромагнітну взаємодію. Розрізняють позитивні та негативні заряди.
Мінімальний електричний заряд, що існує у приро-
ді,— це заряд елементарних частинок — електронів (e).
Електричний заряд будь-якого тіла дорівнює цілому числу
елементарних зарядів (e).
Одиниця виміру заряду в СІ — 1 Кл (1 кулон): 1 Кл = 1 А с ,
e= 1,6 10−19 Кл.
1кулон — це заряд, що протікає через поперечний переріз провідника протягом 1 с при силі постійного струму
в1 А.
Закон збереження заряду: алгебраїчна сума зарядів усіх тіл ізольованої системи залишається незмінною при будьяких процесах чи явищах усередині системи:
q1 + q2 + …+ qn = const .
207
Електродинаміка
1.2.Взаємодія зарядів. Закон Кулона
Різнойменно заряджені тіла і частинки притягуються,
однойменно заряджені — відштовхуються.
Закон Кулона: модуль сили електростатичної взаємодії між двома точковими зарядами q1 і q2 , які містяться у вакуумі, прямо пропорційний добутку модулів їхніх зарядів і обернено пропорційний квадрату відстані r між ними
(рис. 158):
F =k q1 q2 , r2
F1 = −F2 .
rIдеться про взаємодію заряд
|
|
|
|
жених |
тіл |
або |
частинок, а не |
|
|
|
|
|
|||
|
F1 |
F2 |
власне |
зарядів. |
заряди назива- |
||
|
|
|
|
Електричні |
|||
q1 0 |
q2 0 |
ються |
точковими, якщо розпо- |
||||
|
Рис. 158 |
|
|
ділені на тілах, лінійні розміри |
|||
|
|
|
яких значно менші, ніж будь-які |
||||
|
|
|
|
інші розміри в даній задачі. |
|||
|
Коефіцієнт пропорційності в законі |
Кулона (k) — величи- |
|||||
на, яка чисельно дорівнює силі взаємодії двох точкових зарядів по 1 Кл кожний, що розташовані на відстані 1 м один від одного у вакуумі:
|
|
|
k =9 109 |
|
|
Н м2 |
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
Кл2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
У діелектриках сила взаємодії зменшується в ε разів: |
||||||||||||||||||||||||||
|
|
|
F =k |
|
q1 |
|
|
|
|
|
q2 |
|
|
|
|
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
ε r2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
де ε — діелектрична проникність середовища. |
|
|||||||||||||||||||||||||
У теорії електрики k замінюється на k = |
1 |
: |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
F = |
|
|
q1 |
|
|
|
q2 |
|
|
|
|
|
, |
|
4πε0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
4π ε0 ε r2 |
|
|
|
|||||||||||||||||||
ε |
|
= |
1 |
|
=8,85 10−12 |
|
Кл2 |
, |
|
|
||||||||||||||||
0 |
4πk |
|
Н м2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
де ε0 — електрична стала.
208

1. Електростатика
1.3.Електричне поле. Електростатичне поле. Напруженість електричного поля. Принцип суперпозиції полів
Електричне поле — це вид матерії (частковий випадок електромагнітного поля), основною особливістю якої є дія на тіла й частинки, що мають електричний заряд.
Розрізняють два основних види електричних полів:
електростатичне і вихрове (індукційне).
Електростатичні поля — це електричні поля, які існують навколо нерухомих (у даній системі відліку) тіл або частинок, що мають електричний заряд.
Напруженість електричного поля (E) — силова харак-
теристика поля. Це векторна величина, що дорівнює відношенню сили, з якою поле діє на пробний заряд, до величини цього заряду:
|
F |
|
|
=1 |
Н |
|
E = |
q |
, |
E |
Кл . |
||
Пробний заряд — це точковий позитивний заряд, що вноситься в поле.
Сила, з якою діє електростатичне поле, називається кулонівською силою:
F = q E .
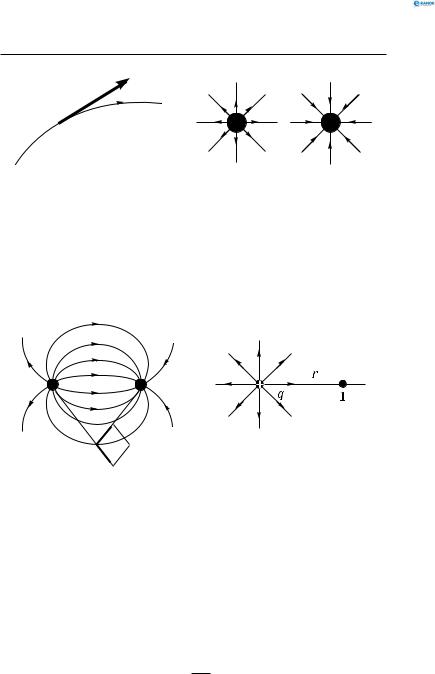
Лінії напруженості (силові лінії) електричного поля — неперервні лінії, дотичні до яких у кожній точці, через яку вони проходять, збігаються з вектором напруженості поля.
Лінії напруженості електростатичного поля починаються на позитивно зарядженому тілі і закінчуються на не-
гативно зарядженому тілі (рис. 159, а, б).
Принцип суперпозиції (накладання): напруженість поля системи зарядів дорівнює векторній сумі напруженостей полів, створюваних кожним із зарядів окремо:
E = E1 + E2 +…+ En .
Поля не взаємодіють, а накладаються. Заряди взаємодіють, оскільки поле одного заряду діє на інший, і навпаки
(рис. 160, а).
209
Електродинаміка
E |
|
+ |
- |
|
|
а |
б |
Рис. 159 |
|
Напруженість поля точкового заряду:
E =k |
|
q |
|
= |
|
q |
|
. |
|
|
|
|
|
|
|||
|
|
|
4πε0εr2 |
|||||
1 |
|
εr2 |
|
|||||
Такий же вигляд має напруженість поля зарядженої сфери, де r — відстань від центра сфери (рис. 160, б).
+ -
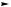
 E2
E2
 E
E
E1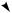
а |
б |
Рис. 160
Напруженість поля нескінченної зарядженої плоскої поверхні (однорідне поле):
E = |
|
σ |
|
|
. |
|
|
|
|||||
2ε0ε |
||||||
|
|
|||||
Поверхнева густина заряду (σ) — це величина, що до-
рівнює електричному заряду, який припадає на одиницю
площі поверхні (рис. 161):
σ = Sq .
210
1. Електростатика
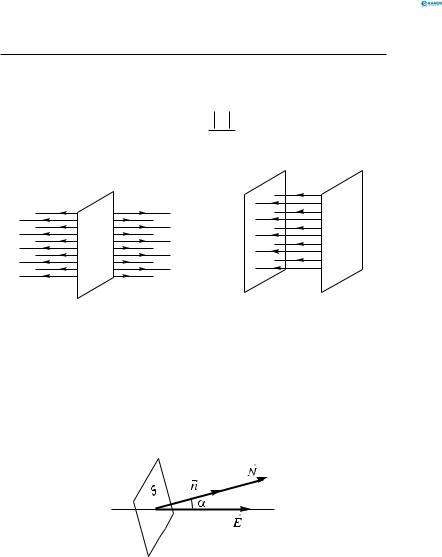
Для рівномірно різнойменно заряджених паралельних нескінченних площин напруженість подвоюється
(рис. 162):
σ
E =2Eпл = ε0ε .
- +
+
Рис. 161 |
Рис. 162 |
В навколишньому просторі E = 0.
Потік вектора напруженості (N) (рис. 163):
N = EScosα,
де α — кут між E і нормаллю n до площини S.
Рис. 163
Теорема Остроградського—Гаусса: потік вектора на-
пруженості через будь-яку замкнену поверхню, яка оточує електричні заряди, дорівнює:
N = |
1 |
∑q . |
|
ε0ε |
|||
|
|
211

Електродинаміка
1.4.Електричне поле у речовині
За здатністю проводити електричні заряди всі речовини умовно поділяються на провідники, діелектрики (непровідники), напівпровідники.
Речовини, де електричні заряди вільно пересуваються, називаються провідниками. Ними є ґрунт, тіло людини, всі
метали у твердому та рідкому станах, водні розчини солей,
кислот, лугів, розплавлені солі та іонізовані гази.
В інших речовинах, названих діелектриками, електричні заряди, надані їм, залишаються на тих самих місцях. Діелектриками є янтар, ебоніт, каучук, фарфор, повітря, су-
хе дерево, капрон тощо.
Є група речовин, які називаються напівпровідниками. При кімнатній температурі напівпровідники мають хоч і дуже малу, проте помітну електропровідність, тобто здатні проводити електричний струм. З підвищенням температури (або при опромінюванні) їхня електропровідність зростає. Напівпровідники займають проміжне місце між провідниками і діелектриками. До напівпровідників належать селен, кремній, германій, закис міді.
1.4.1. Провідники в електростатичному полі (електростатична індукція)
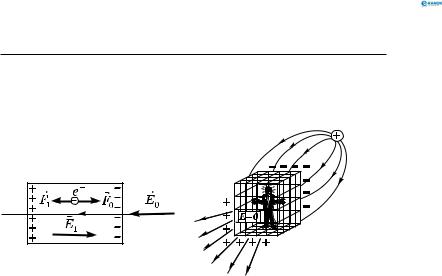
Розглянемо металевий провідник в електричному полі. Металевий провідник складається із позитивних іонів, закріплених у вузлах кристалічної ґратки, і вільних елек-
тронів, які хаотично рухаються в ґратці.
Під впливом зовнішнього електричного поля E0 вільні електрони переміщуються в напрямку, протилежному
напрямку E0. На кінцях провідника виникають заряди: уздовж поля — позитивні (надлишкові іони), проти поля — негативні (надлишок вільних електронів), які утворюють
внутрішнє поле E1 . Процес урівноважується, коли E1 = E0 . Усередині провідника E = E0 − E1 =0, а на його кінцях виникають різнойменні заряди, однакові за модулем (рис. 164):
F1 = F0 ; E1 = E0 ,
E = E0 + E1 E = E0 − E1 =0 ,





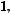
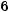

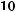

 Кл.
Кл.
212
1. Електростатика
Електростатичний захист — ізоляція від електростатичного поля металевою сіткою і т. п., яка оточує, наприклад, тіло людини, електролампу (рис. 165).
Рис. 164 |
Рис. 165 |
1.4.2. Діелектрики в електростатичному полі (поляризація діелектрика)
Якщо діелектрик складається із полярних молекул (тобто молекули є диполями: на одному кінці переважає по-
зитивний заряд, на другому — негативний), то зовнішнім електричним полем вони орієнтуються вздовж ліній поля
(рис. 166, а).
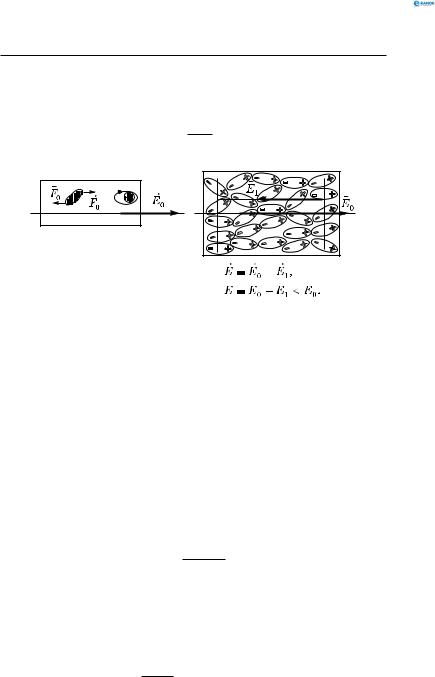
У зовнішньому полі у всіх діелектриків відбувається поляризація молекул (електронні оболонки в атомах і мо-
лекулах зміщуються в напрямку, протилежному E0 ). При цьому всередині діелектрика різнойменні заряди диполів
взаємно компенсуються, а на поверхні утворюються нескомпенсовані зв’язані заряди диполів. Вони утворюють поле
E1 < E0 (рис. 166, б):
E = E0 + E1 ,
E = E0 − E1 < E0 .
Поляризація діелектрика — це виникнення в ньому по-
ля E1 зв’язаних зарядів, яке послаблює зовнішнє поле E0 .
Діелектрична проникність (ε) середовища — це число,
яке визначає, у скільки разів напруженість зовнішнього
213
Електродинаміка
поля E0 більша від напруженості поля в діелектрику. Її величина залежить від виду матеріалу середовища:
ε = EE0 .
а |
б |
Рис. 166
1.5.Робота в електростатичному полі. Потенціал поля. Різниця потенціалів двох точок поля
Робота в електростатичному полі:
—не залежить від шляху, а визначається координатами точок, між якими переноситься заряд;
—у будь-якому замкненому контурі дорівнює нулю. Такі поля називаються потенціальними.
Потенціал поля (ϕ) у даній точці є величина, що чисельно дорівнює роботі кулонівських сил при переміщенні одиничного позитивного заряду з даної точки у нескінченність:
ϕ1 = Aкq1−∞ .
Іншими словами:
Потенціал поля в даній точці є величина, яка чисельно дорівнює потенціальній енергії одиничного позитивного заряду, поміщеного в дану точку, якщо його потенціальну енергію в нескінченності вважати рівною нулю:
ϕ1 = Wqп1
214
1. Електростатика
Потенціал електричного поля точкового заряду q, якщо вважати Wп в нескінченності рівною нулю:
ϕ1 =k εqr , в теорії ϕ1 = 4πεq0εr .
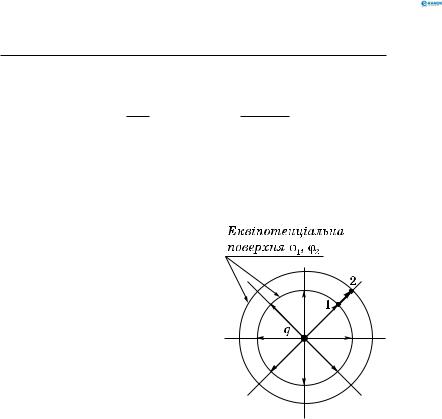
Еквіпотенціальна поверхня — це поверхня, всі точки якої мають однаковий потенціал (рис. 167).
Еквіпотенціальна поверхня і лінії напруженості поля в кожній точці поля взаємно перпендикулярні.
Поверхня електропровідного зарядженого тіла еквіпотен-
ціальна. Робота з переміщення заря-
ду по еквіпотенціальній поверхні дорівнює нулю.
Напруженість у будь-якій точці електростатичного поля дорівнює зміні потенціалу (∆ϕ = ϕ1 −ϕ2 ) , який припадає на одиницю довжини ліній напру-
женості поля (l):
Eх = − |
∆ϕ |
|
= |
В |
|
|
, E |
|
. |
||
l |
м |
||||
Вектор напруженості поля завжди напрямлений у бік змен-
шення потенціалу.
Різниця потенціалів двох точок поля — це величина, яка чисельно дорівнює роботі кулонівських сил при переміщенні одиничного позитивного заряду з першої точки у другу:
|
Aк1−2 |
|
|
Дж |
|
ϕ1 −ϕ2 = |
|
, ϕ |
=1 |
|
=1В . |
q |
Кл |
1.6.Електрична напруга
Сторонні сили — це будь-які сили, крім кулонівських,
які діють на заряд.
Напруга — це величина, яка чисельно дорівнює роботі всіх (кулонівських і сторонніх) сил при перенесенні одиничного позитивного заряду через дану ділянку:
215
