Молекулярна

фізика

1. Основи молекулярно-кінетичної теорії будови речовини

1.1. Основні положення молекулярно-кінетичної теорії та їх дослідне обґрунтування

Розділ фізики, у якому розглядаються закономірності

атомно-молекулярної будови макроскопічних тіл (систем),

називається молекулярною фізикою.

Основоположниками молекулярно-кінетичної теорії є Демо­кріт­ (V—IV ст. до н. е.), М. В. Ломоносов­ (XVIII ст.).

Основні положення молекулярно-кінетич­ної­ теорії:

I положення. Усі речовини складаються з молекул або інших структурних одиниць (атомів, іонів і електронів), розділених проміжками.

Доказом дискретної побудови речовини є фотографії, одержані за допомогою іонного, електронного і тунельного мікроскопів. Про наявність проміжків між молекулами свідчить зміна об’єму твердих тіл і рідини при змінюванні

їхньої температури.

II положення. Молекулиабоіншіструктурнічастинкиперебувають у неперервному хаотичному русі. Підтвердженням

137

Молекулярна фізика

цього положення є явища дифузії, броунівського руху,

осмосу (рис. 117, а).

Дифузія — це процес перерозподілу концентрації атомів у просторі шляхом хаотичної, тобто теплової, міграції.

Осмос — одностороння дифузія.

Броунівський рух — хаотичний рух частинок твердого

тіла, що зависли у рідині або в газі (рис. 117, б). Відкритий у 1827 р. англійським ботаніком Р. Броуном. Спостерігається

в оптичний мікроскоп із збільшенням Г ≈ 500 . Пояснюється поштовхами молекул, які оточують частинку, внаслідок їх неупорядкованого теплового руху.

Рис. 117

IIIположення. Молекули або атоми одночасно­ притягуються і відштовхуються, а рівнодійна цих сил називається­ силою молекулярної взаємодії. Доказом є виникнення

пружних сил при деформації тіл, виникнення сил поверхневого натягу.

1.2.Сили молекулярної взаємодії

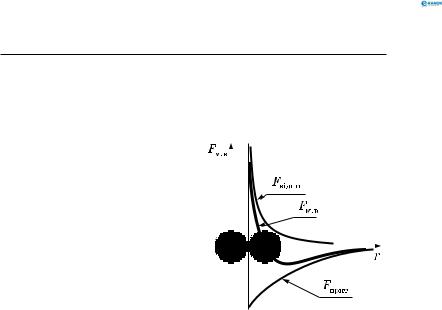
Сили молекулярної взаємодії є силами притягання й відштовхування, залежать від відстані між молекулами і виникають унаслідок взаємодії електричних зарядів, які входять до їх складу. Ці сили є короткодіючими.

138

1. Основи молекулярно-кінетичної теорії будови речовини

Графік залежності сили молекулярної взаємодії Fм.в від відстані між молекулами для найпростіших молекул має такий вигляд (рис. 118).

Якщо r = r0 ≈ dм (dм — діаметр молекули), молекули перебувають у рівновазі.

d0 ≈ 10−10 м.

Молекула — найменша стійка частинка речовини, яка зберігає її основні хімічні

властивості. Вона складається з атомів однакових або різних хімічних елементів, наприклад H2, NaCl, C6H12O6.

Сукупність молекул зберігає фізичні властивості речо-

вини.

Речовина є те, із чого складається фізичне тіло.

Атом — найменша частинка речовини, яка не ділиться при хімічних реакціях, наприклад H, Na, Cl, C, O.

1.3.Маса атомів і молекул

Маси атомів і молекул прийнято порівнювати з 1/12 маси­ ­ атома ізотопу Карбону 126C. Відносною молекулярною масою

Mr називають відношення маси молекули m0 до 1/12 маси атома Карбону m0c (атомної одиниці маси, а. о. м. ) :

Mr — безрозмірна величина.

139

Молекулярна фізика

Маса молекули визначається за допомогою періодичної системи Менделєєва, де вказані відносні атомні маси речовин Mr .

1.4.Молярна маса. Кількість речовини

Один моль — кількість речовини, у якій міститься стільки ж молекул або атомів, скільки в Карбоні 126C масою

0,012 кг.

Стала Авогадро (NA ) — число атомів або молекул в 1 молі будь-якої речовини:

NA =6,02 1023 моль−1 .

Згідно із законом Авогадро 1 моль ідеального газу займає за нормальних умов

( p0 =1,01 105 Па, T =273 К)

об’єм

Vм =22,4 10−3 м3 моль−1 .

Кількість речовини (ν) дорівнює відношенню числа молекул (N) у даному тілі до сталої Авогадро (NА), тобто до числа молекул в 1 молі речовини:

V = N .

NA

Одиниця кількості речовини — 1 моль.

Маса одного моля речовини називається молярною

масою:

M = m0NA ,

або

M = Mr 10−3 молькг .

Одиниця молярної маси — 1 кг/моль.

Маса молекули (в кг) виражена через молярну масу:

m0 = M . NA

140

1. Основи молекулярно-кінетичної теорії будови речовини

Маса тіла (в кг) виражена через масу однієї молекули

і число молекул:

m = m0N.

Кількість речовини (в молях) дорівнює відношенню маси речовини до її молярної маси:

V = Mm .

1.5.Ідеальний газ. Основне рівняння молекулярнокінетичної теорії ідеального газу (рівняння Клаузіуса)

Основне рівняння молекулярно-кінетичної теорії газу (рівняння Клаузіуса) зв’язує мікропараметри (m0,n,v) і макропараметри (p, V, T):

p = 13 m0nv2 ,

де m0 — маса молекули, n — концентрація молекул, v — середня квадратична швидкість руху молекул.

пального руху молекули, то основне рівняння молекулярнокінетичної теорії (МКТ) можна записати у вигляді

p = 23 nEк .

141

Молекулярна фізика

1.6.Температура. Термодинамічна шкала температур і її зв’язок з температурою за міжнародною шкалою

Температура — це величина, яка характеризує теплову рівновагу системи. У всіх частинах системи, що перебуває в тепловій рівновазі, температура однакова.

У молекулярно-кінетичній теорії температура — це величина, зумовлена середньою кінетичною енергією частинок, із яких складається система:

Eк = 32 kT — для одноатомних молекул,

Eк = 52 kT — для двоатомних молекул.

k =1,38 10−23 Дж/К — стала Больцмана, яка зв’язує температуру в енергетичних одиницях з температурою

в кельвінах (T):

θ =kT .

Основне рівняння МКТ, яке виражає залежність тиску газу (p) від концентрації молекул (n) і температури (T):

p = nkT .

Закон Авогадро: у рівних об’ємах газів при однакових температурах і тиску міститься однакова кількість молекул:

Концентрація (n) дорівнює числу частинок в одиниці об’єму:

Температура вимірюється рідинними або газовими термометрами, відповідним чином градуйованими. Висока температура вимірюється оптичними термометрами (за спектром випромінювання) або електричними (напівпровід-

никові термістори, термопари).

У міжнародній шкалі температур за нуль прийнято тем-

пературу танення льоду при нормальному атмосферному тиску, за 100 °С — температуру пари киплячої води при нор-

142

1. Основи молекулярно-кінетичної теорії будови речовини

мальному атмосферному тиску. 1/100 цього інтервалу — це

1 °С (Цельсія). Позначається t °С.

У термодинамічній шкалі­ температур за нуль прийня­ та температура, при якій припинився б тепловий рух частинок, із яких складається тіло.

Ця температура називається абсолютним нулем температур. Оди­

1.7. Середня швидкість теплового руху одноатомних молекул. Дослід ќтерна

Середня швидкість теплового руху одноатомних молекул:

нює добутку сталої Больцмана і сталої Авогадро:

R = k NA .

Дослід Штерна (1920) дає змогу визначити середню швидкість руху молекул експериментально за формулою

де n — частота обертання циліндрів;

143

Молекулярна фізика

RB — радіус більшого циліндра;

RA — радіус меншого циліндра;

S — ширина розмитості смуги срібла.

1.8.Приклади розв’язання задач

Задача 1.

У посудині міститься суміш азоту і водню. При температурі T, коли азот повністю дисоційований­ на атоми, тиск дорівнює p (дисоціацією водню знехтувати). При температурі 3T, коли обидва гази дисоційовані, тиск у посудині дорівнює 4p. Яке відношення мас водню й азоту в суміші?

Якщо T2, коли обидва гази дисоційовані, їх тиск можна подати у вигляді:

144