
- •Передмова
- •МЕХАНІКА
- •1. КІНЕМАТИКА МАТЕРІАЛЬНОЇ ТОЧКИ
- •1.1. Основні поняття
- •1.4. Прямолінійний рух
- •1.5. Криволінійний рух. Рівномірний рух по колу
- •2. ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
- •2.1. Основні закони динаміки. Сила. Рівнодійна сила
- •2.2. Сили в механіці
- •2.4. Алгоритм розв’язання кількісних задач із фізики
- •2.5. Методичні рекомендації щодо розв’язання задач з динаміки
- •2.6. Приклади розв’язання задач
- •3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ
- •3.1. Імпульс тіла. Імпульс сили
- •3.2. Закон збереження імпульсу
- •3.3. Реактивний рух
- •3.4. Енергія. Закон збереження енергії. Види енергії
- •3.5. Види механічної енергії та їх зв’язок з роботою
- •3.6. Механічна робота і потужність
- •3.7. Механічний удар
- •3.8. Прості механізми
- •4. МЕХАНІКА ТВЕРДОГО ТІЛА
- •4.1. Основні поняття
- •4.2. Умови і види рівноваги твердого тіла
- •4.3. Момент імпульсу. Закон збереження моменту імпульсу
- •4.4. Зіставлення рівнянь механіки поступального й обертального рухів (табл. 2)
- •4.5. Приклади розв’язання задач
- •5. ГІДРОСТАТИКА І АЕРОСТАТИКА
- •5.1. Тиск
- •5.2. Закон Паскаля
- •5.3. Гідростатичний тиск
- •5.4. Сполучені посудини
- •5.5. Гідростатичний парадокс
- •5.6. Гідравлічна машина
- •5.7. Закон Архімеда
- •5.8. Умови плавання тіл (табл. 3)
- •5.9. Атмосферний тиск, його вимірювання
- •5.10. Приклади розв’язання задач
- •6. ГІДРОДИНАМІКА І АЕРОДИНАМІКА
- •6.1. Струминна течія рідин і газів
- •6.2. Рівняння Бернуллі
- •6.3. Підйомна сила крила літака
- •6.4. Коефіцієнт лобового опору для тіл різної форми (табл. 4)
- •1. ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ БУДОВИ РЕЧОВИНИ
- •1.1. Основні положення молекулярно-кінетичної теорії та їх дослідне обґрунтування
- •2. ВЛАСТИВОСТІ ГАЗІВ (ГАЗОВІ ЗАКОНИ)
- •2.2. Газові закони
- •2.3. Закон Дальтона
- •2.5. Середня довжина вільного пробігу молекул
- •2.6. Приклади розв’язання задач
- •3. ВЛАСТИВОСТІ ПАРИ
- •3.1. Пара. Випаровування і конденсація
- •3.2. Насичена і ненасичена пара
- •3.3. Вологість повітря (відносна й абсолютна). Точка роси
- •3.4. Кипіння. Перегріта рідина
- •3.5. Приклади розв’язання задач
- •4.2. Поверхнева енергія. Поверхневий натяг
- •4.3. Явище змочування. Капілярні явища
- •4.4. Формула Лапласа
- •4.5. Приклади розв’язання задач
- •5. ВЛАСТИВОСТІ ТВЕРДИХ ТІЛ
- •5.1. Кристалічні та аморфні тіла. Їхні властивості
- •5.2. Типи твердих кристалів
- •5.3. Рідкі кристали
- •5.4. Дефекти кристалічних ґраток
- •5.5. Механічні властивості твердих тіл
- •5.6. Приклади розв’язання задач
- •6. ТЕПЛОВЕ РОЗШИРЕННЯ ТВЕРДИХ І РІДКИХ ТІЛ
- •6.1. Графік залежності потенціальної енергії взаємодії найпростіших молекул від відстані між ними (потенціальна яма)
- •6.2. Лінійне й об’ємне розширення твердих і рідких тіл
- •6.3. Особливості теплового розширення води
- •6.4. Приклади розв’язання задач
- •1.1. Внутрішня енергія ідеального газу
- •1.2. Робота ідеального газу. Її геометричне тлумачення
- •1.5. Питома теплоємність речовини
- •1.6. Питома теплота згоряння палива. ККД нагрівача
- •1.7. Змінювання агрегатного стану речовини
- •2. ПЕРШИЙ ЗАКОН ТЕРМОДИНАМІКИ. АДІАБАТИЧНИЙ ПРОЦЕС
- •3. ДРУГИЙ ЗАКОН ТЕРМОДИНАМІКИ. ЕНТРОПІЯ
- •4. ТЕПЛОВІ ДВИГУНИ
- •ЕЛЕКТРОДИНАМІКА
- •1. ЕЛЕКТРОСТАТИКА
- •1.1. Електричний заряд. Закон збереження заряду
- •1.7. Електризація тіл
- •2. ПОСТІЙНИЙ СТРУМ
- •2.1. Електричний струм. Сила струму. Густина струму
- •2.3. Послідовне і паралельне з’єднання провідників
- •2.4. ЕРС. Закон Ома для повного кола. З’єднання елементів
- •2.6. Приклади розв’язання задач
- •3. СТРУМИ ПРОВІДНОСТІ
- •3.2. Струм в електролітах
- •3.4. Струм у напівпровідниках
- •3.5. Струм у вакуумі (струм переносу)
- •3.6. Приклади розв’язання задач
- •4. МАГНЕТИЗМ
- •4.1. Магнітне поле. Магнітна індукція поля
- •4.2. Магнітне поле струму
- •4.3. Дія магнітного поля на рухомий заряд (сила Лоренца) і провідник зі струмом (сила Ампера). Правило лівої руки
- •4.4. Дія магнітного поля на рамку зі струмом. Магнітний потік
- •4.5. Закон взаємодії паралельних струмів
- •4.6. Магнітне поле у речовині
- •4.7. Приклади розв’язання задач
- •5. ЕЛЕКТРОМАГНІТНА ІНДУКЦІЯ
- •5.1. Явище електромагнітної індукції. Вихрове електричне поле
- •5.3. Індукційні струми в суцільних провідниках
- •5.4. Самоіндукція. Індуктивність. Енергія магнітного поля
- •5.5. Електромагнітне поле. Теорія Максвелла в якісному вигляді
- •5.6. Приклади розв’язання задач
- •ФІЗИКА КОЛИВАНЬ
- •1. КОЛИВАЛЬНИЙ РУХ
- •1.1. Основні поняття
- •1.2. Гармонічні коливання
- •2. ЗМІННИЙ СТРУМ
- •2.1. Одержання змінного синусоїдного струму. Закономірності змінного струму
- •2.2. Діюче значення змінного струму
- •2.3. Опір змінному струму. Закон Ома для змінного струму
- •2.4. Електричний резонанс. Резонанс напруг. Резонанс струмів
- •2.5. Випрямлення змінного струму
- •2.6. Трансформація змінного струму
- •2.7. Змінний струм високої частоти
- •2.8. Приклади розв’язання задач
- •3. ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ
- •3.2. Закономірності вільних електромагнітних коливань. Згасаючі коливання
- •3.3. Отримання незгасаючих електромагнітних коливань
- •3.4. Приклади розв’язання задач
- •4. МЕХАНІЧНІ ХВИЛІ. ЗВУК
- •4.1. Поздовжні і поперечні хвилі. Промінь. Довжина хвилі. Фронт хвилі
- •4.2. Принцип Гюйгенса
- •4.3. Інтерференція хвиль
- •4.4. Дифракція хвиль
- •4.5. Звук. Звукові хвилі. Інтенсивність, висота і тембр звуку
- •4.6. Луна. Звуковий резонанс
- •4.7. Приклади розв’язання задач
- •5. ЕЛЕКТРОМАГНІТНІ ХВИЛІ
- •5.1. Випромінювання електромагнітних хвиль відкритим коливальним контуром
- •5.3. Принцип радіозв’язку. Модуляція і детектування (демодуляція)
- •5.4. Класифікація радіохвиль і особливості їх поширення
- •5.5. Приклади розв’язання задач
- •ОПТИКА
- •1. ХВИЛЬОВА ОПТИКА
- •1.1. Монохроматичне світло. Заломлення світла
- •1.2. Дисперсія світла
- •1.4. Інтерференція білого світла за Френелем
- •1.5. Інтерференція білого світла за Ньютоном. Кільця Ньютона
- •1.6. Дифракція білого світла
- •1.7. Поляризація світла
- •2. ГЕОМЕТРИЧНА ОПТИКА
- •2.2. Закони відбивання світла
- •2.3. Закони заломлення світла. Повне відбивання світла
- •2.4. Хід променів через плоскопаралельну пластинку, призму
- •2.5. Сферичні лінзи
- •2.6. Око як оптична система
- •2.8. Сферичні дзеркала
- •2.9. Приклади розв’язання задач
- •3. ВИПРОМІНЮВАННЯ ТА СПЕКТРИ
- •3.1. Люмінесценція
- •3.2. Інфрачервоні та ультрафіолетові промені
- •3.3. Рентгенівські промені
- •3.4. Спектри випромінювання. Спектри поглинання
- •3.5. Спектральний аналіз
- •1.1. Поняття про простір і час
- •1.2. Постулати СТВ. Перетворення Лоренца
- •1.4. Приклади розв’язання задач
- •2. КВАНТОВА ОПТИКА
- •2.1. Теорія Планка. Імпульс фотона
- •2.2. Фотоефект
- •2.3. Фотоелементи та їх застосування
- •2.4. Світловий тиск
- •2.5. Корпускулярно-хвильовий дуалізм
- •2.6. Хімічний вплив світла. Чорно-біла фотографія. Фотосинтез. Ланцюгові реакції
- •2.7. Приклади розв’язання задач
- •3. ФІЗИКА АТОМА
- •3.1. Планетарна модель атома Резерфорда
- •3.2. Постулати Бора. Борівські орбіти
- •3.3. Атом Гідрогену за Н. Бором
- •3.4. Приклади розв’язання задач
- •4. ФІЗИКА АТОМНОГО ЯДРА
- •4.1. Відкриття протона і нейтрона
- •4.2. Теорія будови ядра
- •4.3. Енергія зв’язку ядра. Дефект маси
- •4.4. Природна радіоактивність
- •4.6. Часткове звільнення внутрішньоядерної енергії при екзотермічних ядерних реакціях
- •4.7. Закон радіоактивного розпаду
- •4.8. Приклади розв’язання задач
- •5. ЕЛЕМЕНТАРНІ ЧАСТИНКИ
- •5.1. Фізика елементарних частинок
- •5.2. Приклади розв’язання задач
- •Предметний покажчик
Механіка
4.3. Момент імпульсу. Закон збереження моменту імпульсу
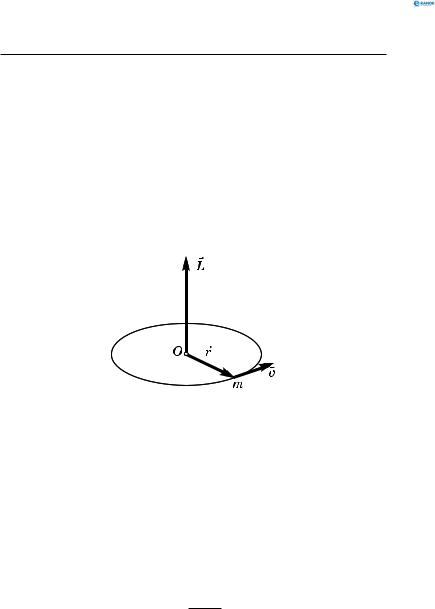
Момент імпульсу матеріальної точки L з масою m, яка рівномірно обертається зі швидкістю v по колу радіусом r
(рис. 80):
Закон збереження моменту імпульсу для ізольованої
системи тіл:
N
∑Jiω2 = const ,
i=1
Рис. 80
Робота постійного моменту сили, яка діє на тіло, що
обертається: = ϕ
A M ,
де M — момент сили; ϕ — кут обертання.
Потужність при рівномірному обертальному русі:
N = Mω .
Кінетична енергія обертального руху:
Eк = J2ω2 .
Кінетична енергія поступального руху центра мас і обертального руху тіла:
Eк = |
mv2 |
+ |
Jω2 |
. |
|
2 |
2 |
||||
|
|
|
104

4. Механіка твердого тіла
4.4. Зіставлення рівнянь механіки поступального й обертального рухів (табл. 2)
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 2 |
|
|
|
|
|
|
|
|
|
|
|||||
Поступальний рух |
Обертальний рух |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Маса m |
Момент інерції J |
|
|||||||||||
Сила F |
Момент сили M |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Імпульс p =mv |
|
|
|
|
|
|
|
||||||
Момент імпульсу L = Jω |
|||||||||||||
|
|
|
|
|
|
Перший закон Ньютона |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
N |
|
|
v = const , якщо ∑Fi =0 |
ω= const , якщо ∑Mi |
=0 |
|||||||||||
|
|
|
|
|
i=1 |
|
|
|
|
i=1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Другий закон Ньютона |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
=ma |
N |
|
|
= Jε |
|
|||||
∑Fi |
∑Mi |
|
|
||||||||||
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Третій закон Ньютона |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
F12 = −F21 |
M12 = −M21 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Закон збереження |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
імпульсу |
моменту імпульсу |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
= const |
N |
|
|
|
|
|
||||
∑m1v1 |
∑J1ωi = const |
|
|||||||||||
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Робота |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A = FS |
A = Mϕ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кінетична енергія |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eк |
= |
|
mv2 |
Eк |
= |
|
Jω2 |
|
|||||
|
2 |
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Потужність |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N = |
|
A |
= Fv |
N = |
A |
|
= Mω |
|
|||||
|
|
t |
|
|
|||||||||
|
|
t |
|
|
|
|
|
|
|
|
|||
105
Механіка
4.5. Приклади розв’язання задач
Задача 1.
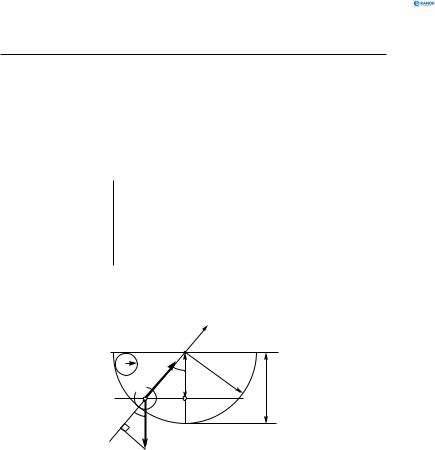
Тонкий обруч радіусом r без проковзування скочується в яму, яка має форму напівсфери з R r . На якій глибині сила тиску обруча на стінку дорівнює його вазі спокою на Землі?
Дано: |
Розв’язання: |
r |
h = Rcosα , оскільки розмірами об- |
Rруча r можна знехтувати за умовою задачі. За третім законом Ньютона P = N, але
R r |
|
P = mg в спокої на Землі. |
h — ? |
|
|
|
|
|
Запишемо |
основне рівняння динаміки для обруча |
|
(рис. 81): |
|
N +mg =maдоц . |
|
|
|
|
|
|
x |
|
r |
|
O |
|
R |
|
N |
h |
||
|
C |
|
R |
|
|
A |
|
||
|
|
|
|
|
mg
|
|
|
Рис. 81 |
|
|
|
|
|
|
||
У проекції на вісь Ox: |
|
|
|
|
|
|
|||||
|
N −mgcosα =maдоц . |
|
(1) |
||||||||
Оскільки aдоц = |
v2 |
і N =mg, то mg −mgcosα = |
mv2 |
|
, |
||||||
|
R |
|
|||||||||
|
R |
v2 |
|
|
|
|
|||||
|
g(1−cosα) = |
. |
|
|
(2) |
||||||
|
|
|
|||||||||
|
|
|
|
|
|
R |
|
|
|
||
Приймемо за нульовий рівень потенціальної енергії рі- |
|||||||||||
вень, який проходить через точку A. |
|
|
|
||||||||
Запишемо закон збереження механічної енергії: |
|
|
|
||||||||
|
mgh = |
mv2 |
+ |
|
Jω2 |
. |
|
(3) |
|||
|
|
|
|
|
|||||||
2 |
|
|
2 |
|
|
|
|
|
|||
106
4. Механіка твердого тіла
Для кільця момент інерції дорівнює:
Jкільця =mr2 , а ω= vr .
Тоді
mgh = |
mv2 |
+ |
mr2v2 |
= |
mv2 |
+ |
mv2 |
=mv2 , |
|
2 |
2r2 |
2 |
2 |
||||||
|
|
|
|
|
mgh =mv2 , v2 = gh .
Підставимо значення v2 в рівняння (2): g(1−cosα) = ghR , 1−cosα = Rh .
Із OAC :
cosα = Rh 1− Rh = Rh , 1= 2Rh .
Звідси: h = R2 .
Відповідь: сила тиску обруча на стінку напівсфери дорівнює вазі спокою відносно Землі на висоті, що дорівнює половині її радіуса.
Задача 2.
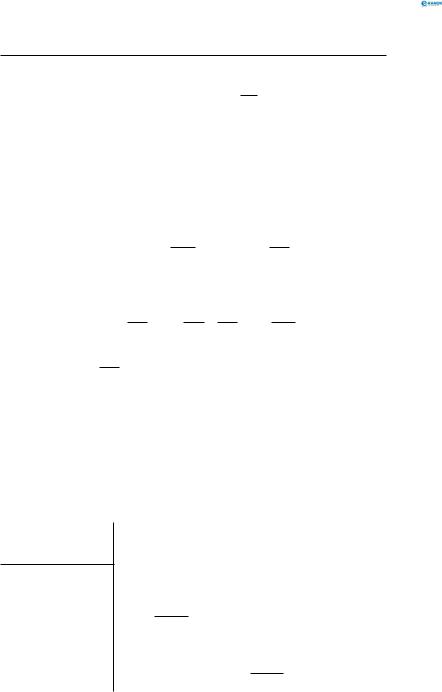
Стовп заввишки l падає із вертикального положення. Визначити швидкість падіння верхнього кінця при ударі об землю, якщо нижній кінець при падінні не переміщується.
Дано:
l
v — ?
Розв’язання:
Потенціальна енергія стовпа у вертикальному положенні (Eп =mgh) дорівнює
кінетичній енергії при ударі об Землю
( Eк = J2ω2 , оcкільки Eк поступального руху центра маси дорівнює нулю):
mgh = J2ω2 .
107
Механіка
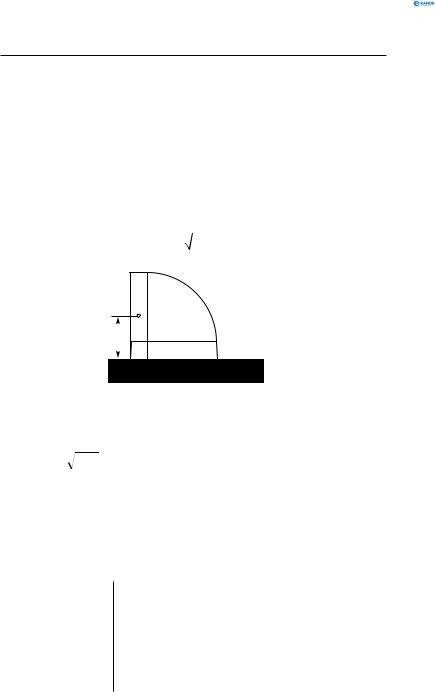
Оскільки h = |
l |
(рис. 82) і момент інерції стрижня за- |
|
2 |
|||
|
|
вдовжки l відносно осі, яка перпендикулярна до стрижня і проходить через його кінець, дорівнює:
J = |
ml2 |
|
, а ω= |
|
v |
|
= |
|
v |
, |
||||
3 |
|
|
|
|
|
|
l |
|||||||
|
|
|
|
|
|
R |
|
|
||||||
отже, |
|
|
l |
|
|
ml2 |
|
|
|
v2 |
|
|
||
mg |
|
|
= |
|
|
|
. |
|
||||||
|
2 |
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
l22 |
|
|
|
||||
Звідси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = |
3gl . |
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2 Eï 0 |
|
Рис. 82
Відповідь: швидкість верхнього кінця стовпа при ударі об землю v = 3gl .
Задача 3.
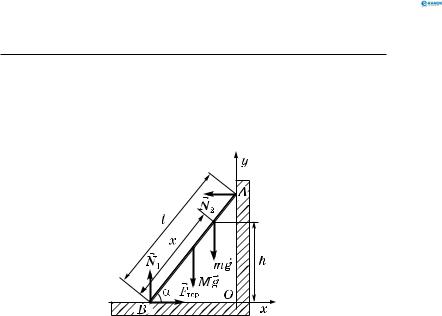
На яку максимальну висоту може піднятися людина масою m по драбині масою M і завдовжки l, приставленій до гладенької стіни? Кут між драбиною і підлогою дорівнює α, коефіцієнт тертя об підлогу дорівнює µ.
Дано: |
Розв’язання: |
m |
Запишемо умови рівноваги драбини: |
M |
1) алгебраїчна сума моментів сил від- |
lносно точки B дорівнює нулю (рис. 83):
α |
M1 + M2 + M3 + M4 + M5 = 0 , |
µ |
|
|
|
h — ? |
|
108
4. Механіка твердого тіла
−N2lsinα +mgxcosα + Mg |
lcosα |
=0 . |
(1) |
|
2 |
||||
|
|
|
Моменти сил N1 і Fтер дорівнюють нулю, оскільки дорівнюють нулю плечі цих сил відносно точки B;
Рис. 83 |
2) векторна сума сил, які діють на драбину, дорівнює нулю:
mg + Mg + N2 + Fтер + N =0 .
Проекція цього рівняння на вісь Ox:
Fтер − N2 =0 Fтер =µN1 ,
отже,
N2 =µN1 . |
(2) |
Проекція рівняння на вісь Oy: |
|
N1 − Mg −mg =0 |
, |
N1 = g(M +m) . |
(3) |
Підставимо значення N1 в N2 , дістанемо:
N2 =µg(M +m) .
109

Механіка
Підставимо значення N2 в рівняння (1):
−µg(M +m)lsinα +mgxcosα + Mg lcos2 α =0 ,
mxcosα =µ(M +m)lsinα − Mlcosα , 2
|
|
|
|
|
|
Mcosα |
|
|
|||||||
|
|
µ(M +m)sinα − |
|
|
|
|
|
|
l |
|
|
||||
|
|
2 |
|
|
|
|
|||||||||
x = |
|
|
|
|
|
|
|
|
. |
|
|||||
|
|
mcosα |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Шукана висота: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Mcosα |
|
|
||||
|
|
|
µ(M +m)sinα − |
|
|
|
|
|
l |
||||||
|
|
2 |
|
|
|
||||||||||
h = xsinα = |
|
|
|
|
|
|
|
|
|
|
sinα , |
||||
|
mcosα |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Mcosα |
|
|
|
|||||||||
|
(M +m)µsinα − |
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
||||||||||
h = |
|
|
|
|
|
|
l tgα . |
||||||||
|
m |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відповідь: максимальна висота, на яку піднімається людина, дорівнює:
h =
Задача 4.
|
Mcosα |
|||
(M +m)µsinα − |
|
|
||
2 |
||||
|
|
l tgα . |
||
m |
|
|
||
|
|
|
||
В однорідній тонкій круглій пластинці радіусом r вирі-
зано круг радіусом 2r . Визначити положення центра маси
Дано: |
|
Розв’язання: |
|
|
|||
R = r |
|
Вкладемо круг у виріз пластини. |
|
R1 = |
r |
= OO1 |
Тоді сила тяжіння великого диска |
2 |
mg =m1g +m2g . |
||
x — ? |
|
||
|
|
||
x = OC |
|
|
|
|
|
|
|
110

4. Механіка твердого тіла
За правилом моментів сил (відносно точки O):
M1 + M2 + M3 =0 , M1 = −m1gR1 = −m1g 2r
Оскільки сила тяжіння великого диска (mg) проходить через точку O, то момент цієї сили (M2 ) дорівнює нулю:
M3 =m2gx (рис. 84).
Тоді −m1g 2r +m2gx =0 .
Звідси випливає:
m2gx =m1g 2r ,
x = m1r . 2m2
Виразимо маси і об’єми тіл:
m1 =ρV1 , m2 =ρV2 , V1 = S1h , V2 = S2h .
A |
O1 |
O Ñ |
B |
|
|
2r |
|
|
|
r/2 |
x |
A |
O1 |
O Ñ |
B |
|
|
m1g |
|
|
|
|
m2g |
|
|
mg |
|
|
|
Рис. 84 |
|
111
