30. Тензори в криволінійних просторах

Перейдемо від криволінійної системи /стара система/ до системи/нова система/, тоді

, /30.1/

, /30.2/

Ми записали, по суті, закон перетворення контраваріантних складових вектора при переході від однієї криволінійної системи до іншої. За таким же законом повинні перетворюватися контраваріантні складові будь-якого вектора, отже,

, /30.3/

. /30.4/

-103

Щоб знайти закон перетворення коваріантного вектора, розглянемо скалярну функцію . Змінапри нескінченно малому переміщеннідорівнює

. /30.5/

Ліва сторона /30.5/ є інваріантом, отже мусить бути коваріантним вектором. Закон його перетворення має вигляд

. /30.6/

Цей же закон справедливий і для довільного коваріантного вектора

, /30.7/

і, очевидно,

. /30.8/

Одержані формули нагадують відомі закони перетворення з теорії косокутних координат

, ,

, .

Таким чином, можна вважати, що

,

, /30.9/

однак, тепер коефіцієнти івже не є сталими

,

. /30.10/

-104-

Легко переконатися, що залишаються справедливими формули, які зв’язують коефіцієнти і:

.

Приклад. Переконаємось, що скалярний добуток ко- і контраваріантного векторів є інваріантом і в криволінійному просторі. Ми маємо:

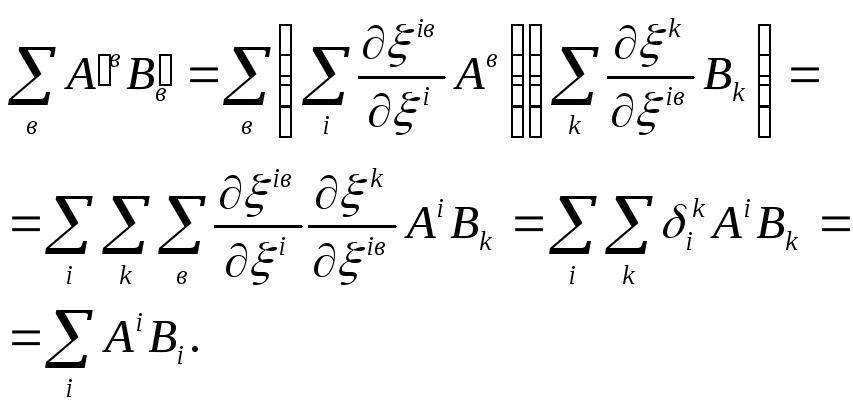
Формули /30.3/ - /30.4/ і /30.7/ - /30.8/ є, по суті, означенням контра- і коваріантного векторів у криволінійних просторах, тобто є означення тензорів першого рангу. Не представляє труднощів записати закони перетворення тензорів вищих рангів.

Компоненти тензорів другого рангу перетворюються за законами

,

,

, /30.11/

,

,

.

У загальному випадку

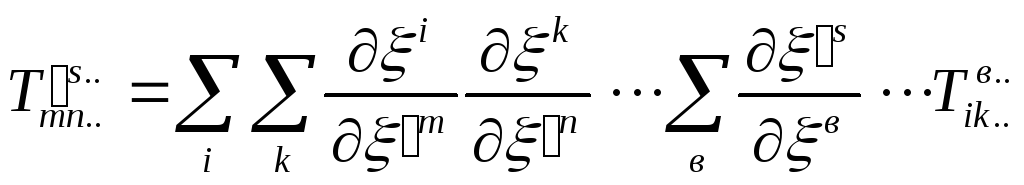. /30.12/

-105-

Ранг тензора можна понизити на дві одиниці за допомогою операції згортання

. /30.13/

Щоб довести це, у формулі /30.12/ проведемо сумування по індексах і

• ми одержали закон перетворення тензора рангу .

Очевидно вирази

,

тензорної розмірності не мають.

Розглянемо тепер мішані похідні і знайдемо їх трансформаційні властивості. Ми маємо

тобто

. /30.14/

Як видно, мішані похідні не є компонентами тензора. Однак, у випадку косокутних координат, коли

-106-

/старі і нові координати зв’язані лінійними співвідношеннями/, формула /30.14/ дає закон перетворення коваріантного тензора другого рангу /пор.§27/.

Цікаво відзначити, що різниця

Є коваріантним антисиметричним тензором другого рангу /ротор у криволінійних координатах/. Дійсно, при переході до нової системи ми одержуємо закон перетворення тензора другого рангу

Зауважимо, що мішані похідні , і навіть їх різниця

не є тензорами, що легко перевірити аналізуючи трансформаційні властивості цих виразів.

Звичайно, причинні зв’язки слід встановлювати, виходячи з досвіду, але ми не повинні відмовлятися від обов’язку виправляти й доповнювати наше розуміння спостережуваних явищ подальшим міркуванням.

Б.Ріман

31. Метричні простори

Розглянемо дві нескінченно близькі точки в просторі декартових координат. Віддаль між ними визначається відомою формулою

. /31.1/

-107-

При переході до криволінійних координат

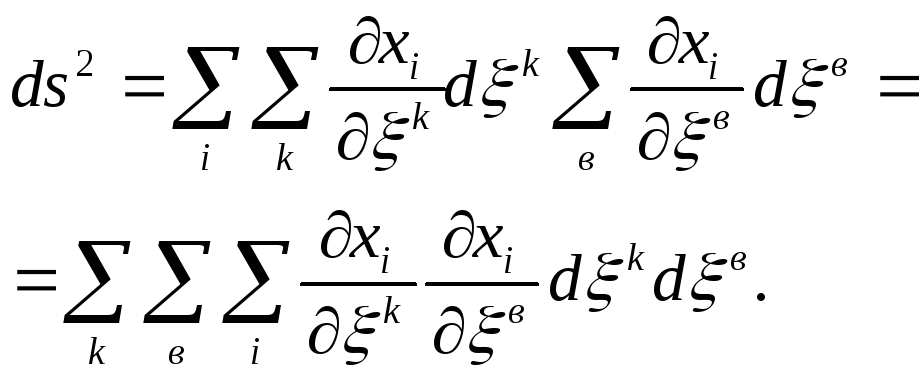
Дев’ять величин

, /31.2/

як відомо, називають коваріантними складовими метричного тензора, вони задають метрику криволінійного простору. Таким чином,

. /31.3/

Здійснимо зворотній перехід від криволінійної до декартової системи. Ми знову приходимо до формули

,

тобто добиваємось того, що метричний тензор переходить у символ Крон екера

.

Існують простори, в яких не можна ввести декартової системи координат. Класичним прикладом такого простору є двомірна поверхня сфери. Положення точки на сфері визначається двома кутами і.

-106-

Тоді

– квадрат диференціала дуги заданий як однорідна квадратична форма координат.

Подібні простори називаються метричними або рімановими. Таким чином, метричний простір задається дев’ятьма складовими метричного тензора

,

причому

Рис. 78

.

Якщо в метричному просторі можна ввести таку систему координат, для якої , то ця система буде декартовою, а простір – евклідовим. З цієї точки зору, простір, визначений циліндричними координатамиє евклідовим, тому що завжди можна перейти до декартових координат за відомими формулами

, ,

Евклідові простори є тільки класом метричних просторів.

Переконаємось, що поняття метричного тензора не зв’язане з існуванням декартової системи координат. Нехай простір метричний

Здійснимо перетворення координат, тоді

,

.

З другого боку

.

Порівнюючи обидва вирази для маємо

-107-

(31.4)

– перетворюється як коваріантний тензор.

Контраваріантний метричний тензор вводиться в метричному просторі за допомогою співвідношень

(31.5)

Звідси випливає, що

,

де

.

Метричний простір, для якого

називають ортогональним. Як легко перевірити, для такого простору

Розглянемо довільний вектор у точціметричного простору, визначеній координатами. Його ко- і контраваріантні складові це відповідно узагальнені проекції і узагальнені складові по напрямках векторів локального репера. Їх трансформаційні властивості визначаються формулами (30.3) – (30.4) і (30.7) – (30,8). Зв'язок між ними здійснюється за допомогою операцій піднімання і опускання індекса

, (31.6)

Шість, маленьке два,

хрестик і закарлючка.

Господи, от голова була…

Скільки тут таємниць…

Уееллс. Людина-невидимка

32. Задача про паралельне перенесення вектора

Ми з’ясували, що звичайні похідні від скалярного поля є складовими коваріантного

-108-

векторного поля. Однак, вже мішані похідні від векторного поля, і тим більше мішані похідні від тензорного поля другого і вищих рангів, не утворюють тензорного поля в криволінійному просторі.

Наша задача полягає в тому, щоб одержати нові тензорні поля в результаті диференціювання, тобто нам треба розробити такий метод диференціювання тензора, який приводить до тензорів вищих рангів.

Попередньо нам треба розв’язати доволі складну задачу про паралельне перенесення вектора. Загальності будемо розглядати вектор у метричному просторі, визначеному метричним тензором.

Рис. 79

Кожній точці простору відповідає свій локальний репер, визначений векторами . Дійсно, якщо заданий тензорми завжди знайдемо довжину векторів

і кути між ними

.

Перенесемо паралельно вектор з точкив нескінченно близьку точку. Очевидно, сам вектор не зміниться, однак його ко- і контраваріантні складові змінюються за рахунок зміни репера. Ці зміни позначимо відповідно черезі.

Зробимо цілком логічне припущення: зміна складової вектора повинна бути однорідною квадратичною функцією складових вектора і диференціалів координат

(32.1)

(32.2)

де і– набори якихось невідомих коефіцієнтів.

Переконаємось насамперед, що

Для цього розглянемо згортку двох векторів і

і перенесемо паралельно обидва вектори з точки у точку

-109-

Підставимо сюди вирази (32.1) і (32.2)

.

В другому члені правої сторони цієї рівності пере позначимо німі індекси і( індексзамінимо на, індекс– на), тоді

.

Тому що – довільні, ми і одержуємо (32.3)

Таким чином, закон паралельного перенесення вектора можна записати у вигляді

(32.4)

(32.5)

Поки що ми знаємо про коефіцієнти , тільки те, що вони є функціями координат

(32.6)

Знайдемо їх трансформаційні властивості.

Перейдемо від системи до нової системи. У новій системі

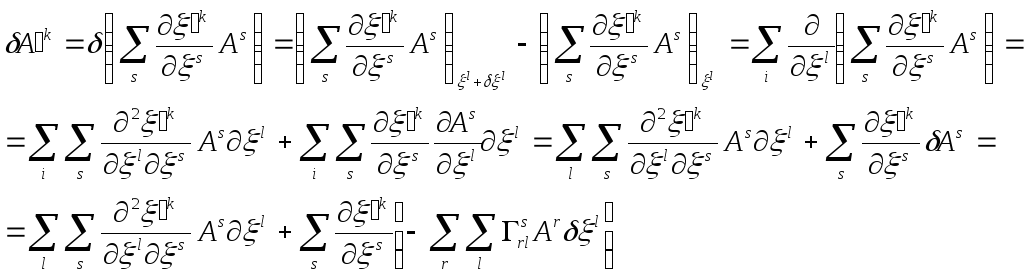
Перепозначимо індекси сумування в останній групі доданків, тоді

(32.8)

-110-

Підставляючи у формулу (32.7)

, ,

одержимо

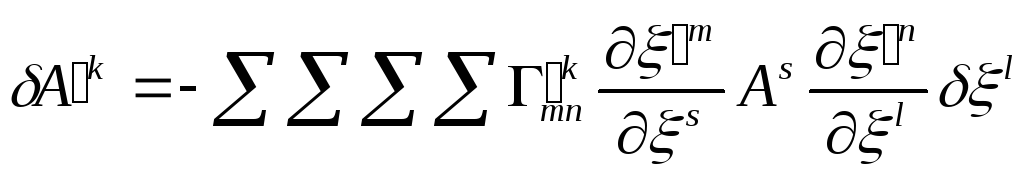(32.9)

Праві сторони (32.8) і (32.9) мусять збігатися, бо

Величини ідовільні, тому вираз у фігурній дужці дорівнює нулеві. Отже,

.

Щоб знайти вираз помножимо одержану рівність на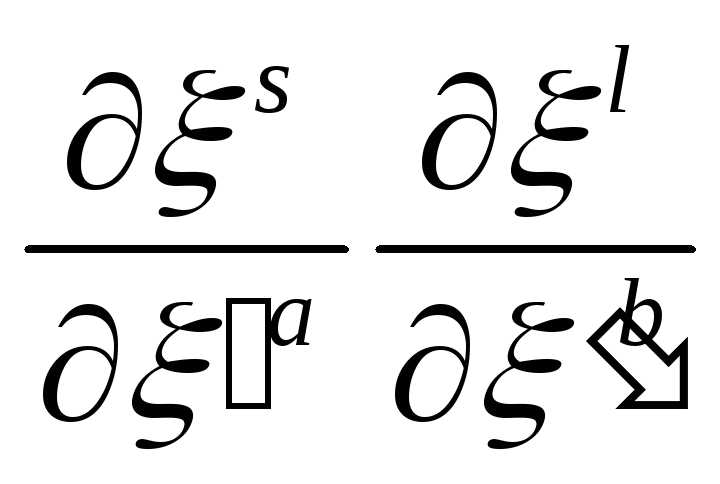і просумуємо результат поі, тоді

Таким чином,

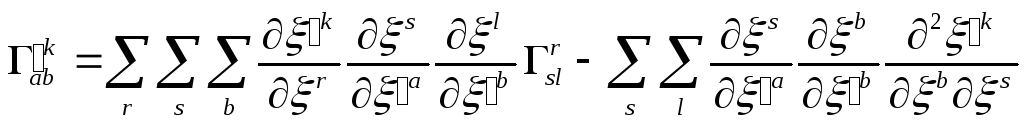
Перетворимо ще останню групу доданків

Остаточно закон перетворення коефіцієнтів має вигляд

(32.10)

Формула (32.10) у правй частині має дві групи доданків. Перша група має такий же вигляд, як закон перетворення мішаного тензора

-111-

третього рангу. Вираз

не залежить від і симетричний відносно долішніх індексів. Наявність цього виразу свідчить про те, щоне є тензором.

Якщо існує така система координат, в якій

то

Тоді рівність

залишається справедливою в усіх інших координатних системах. Для цього досить, щоб у метричному просторі можна було ввести таку систему координат, в якій хоча б локально.

Величини називають коефіцієнтом афінного зв’язку. Якщо

(32.11)

афінний зв'язок називають симетричним. Далі ми обмежимось розглядом тільки симетричного афінного зв’язку.

Наш досвід переконує нас, що природа – це реалізація найпростіших математичних ідей.

А. Ейнштейн

33. Символи Крістоффеля. Класифікація просторів

Величини можна визначити однозначно, якщо пов’язати їх з метричним тензором.

Нехай у метричному просторі заданий закон паралельного перенесення вектора

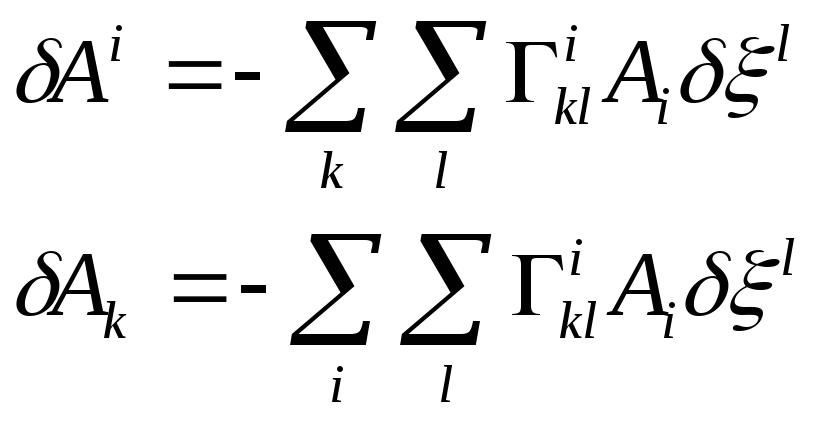(33.1)

При переході від точки до точки

,

-112-

тобто

Відкинемо доданок другого порядку мализни , тоді

Підставляючи сюди

і вирази (33.1) і (33.2), одержимо

Далі підставимо

,

і тоді

а тому що ідовільні

Останню рівність запишемо три рази змінюючи індекси

,

,

.

Віднімемо від першого рівняння друге і третє, одержимо

,

.

Щоб визначити помножимо цю рівність наі просумуємо по. Тоді

,

і остаточно

-113-

(33.3)

Цей вираз називають символом Крістоффеля другого роду і позначають через

(33.4)

Вираз

(33.5)

називають символом Крістоффеля першого роду. Очевидно, що

(33.7)

Таким чином, ми познайомились з такими класами просторів:

1. декартовий (евклідовий)

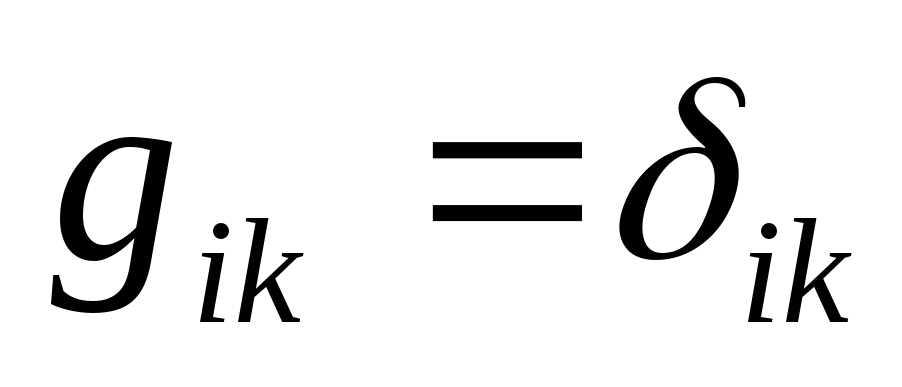
2. плоский (псевдо евклідовий)

3. криволінійний

4. метричний

5. афінного зв’язку

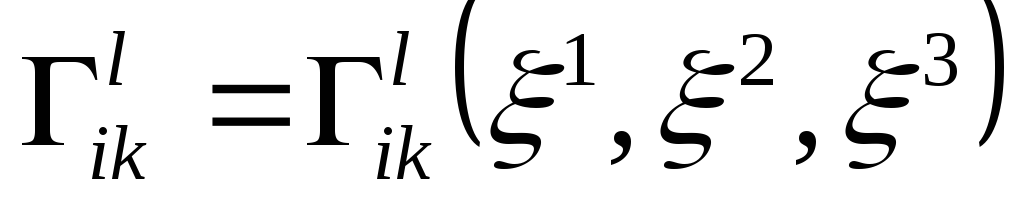
а) симетричний

б) несиметричний

Всі наші міркування, всі результати і одержані формули не важко узагальнити на простори n вимірів. Особливий інтерес для фізики представляє чотирьохмірний простір Мінковського, інтервал в якому заданий формулою

Якщо прийняти

, ,,,

то метрика такого простору задана тензором

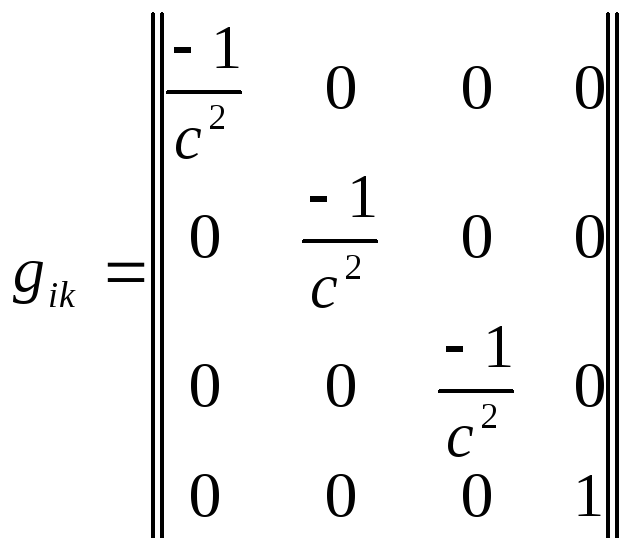
-114-

а сам простір Мінковського треба розглядати як чотирьохмірний, плоский, псевдо евклідовий простір.

У загальній теорії відносності основний є припущення про те, що реальний фізичний простір є чотирьохмірним метричним простором. Складені метричного тензора такого простору є функціями чотирьох координат, і вигляд залежить від розподілу речовини в просторі. Основна задача загальної теорії відносності і полягає у визначенні складових ,якщо відомий розподіл речовини.

Чоловік з дружиною піднялися на високу гору.

– Поглянь яка краса, який краєвид! Які чудові сади, хатини, річка!

Дружина зі злістю:

Якщо там така краса, то якого біса, ти заставив мене карабкатися на цю високу гору?

/З книги єврейського гумору/

34. Коваріантне диференціювання

Мішана похідна від тензора рангу N (N≥1) не є тензором. Однак можна утворити певні тензори, які відіграють роль звичайних похідних від тензорів.

Відзначимо, що закон паралельного перенесення

можна поширити на тензор довільного рангу. Проілюструємо це на прикладі мішаного добутку двох векторів , який є мішаним тензором другого рангу. При «паралельному перенесенні» такого добутку його складові зазнають зміни

а, взагалі, для тензора другого рангу

Закон паралельного перенесення тензора третього рангу матиме вигляд

-115-

Подібні формули можна записати і для тензорів вищих рангів.

Розглянемо для конкретності мішаний тензор другого рангу в точці. Перенесемо його паралельно в точкуодержимо

У точці тензор набуває значення

Різниця цих виразів

дорівнює

Вираз, що стоїть у дужці є тензором третього рангу і його називають коваріантною похідною тензора

/34.1/

Обмежуючись розглядом метричних просторів, ми можемо замінити коефіцієнти афінного зв’язку символами Крістоффеля другого роду.

Тоді

/34.2/

Щоб одержати коваріантну похідну тензора довільного рангу треба до звичайної похідної додати додаткові члени. Кожному контраваріантному індексові відповідає доданок

/34.3/

а кожному коваріантному індексові – доданок

/34.4/

Приклад. Коваріантною похідною тензора в тензор п’ятого рангу

Коваріантні похідні суми і добутку обчислюються за такими ж правилами як і звичайні похідні

/34.5/

-116-

/34.6/

Наприклад,

Легко переконатися, що коваріантна похідна від метричного тензора дорівнює нулеві

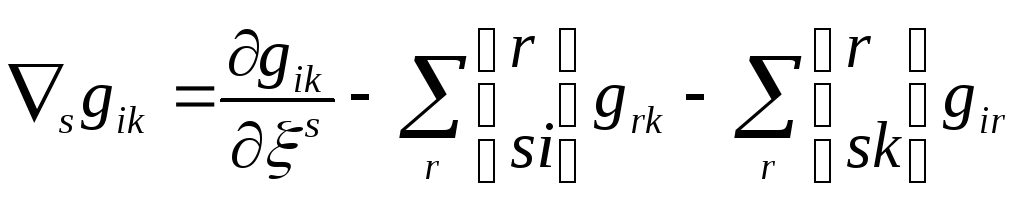
а цей вираз дорівнює нулеві /див. 33/. Таким чином,

/34.7/

При коваріантному диференціюванні добутку метричний тензор поводиться як стала величина

Доведемо, що коваріантна похідна тензора дійсно має тензорну розмірність. Для цього використаємо рівність /32.10/

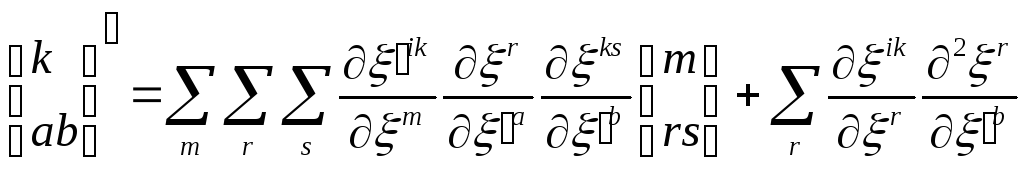
Помножимо її на і просумуємо поk

Звідси

/34.8/

-117-

Продиференціюємо по рівність

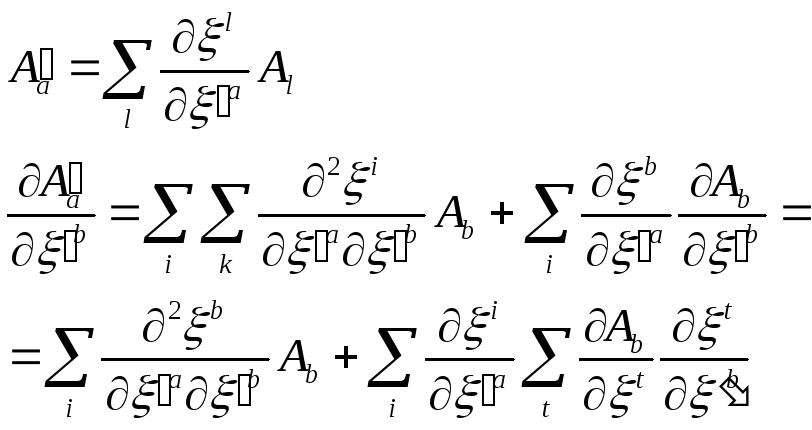
Підставимо сюди /34.8/ і пере позначимо індекси в останній групі доданків

Тут

отже,

Звідси зрозуміло, що вираз

перетворюється як коваріантний тензор другого рангу. Аналогічним чином можна показати тензорний характер коваріантних похідних від тензорів вищих рангів.

Для декартового і косокутного просторів, коли , символи Крістоффеля дорівнюють нулеві і коваріантні похідні збігаються зі звичайними. У випадку скалярного поля звичайна похіднав коваріантним тензором першого рангу.Власне тому для оператора коваріантної похідної ми зберегли символ набла – оператор коваріантної похідної в узагальненням оператора набла.

-122-

Приклад 2. Сферичні координати

,,

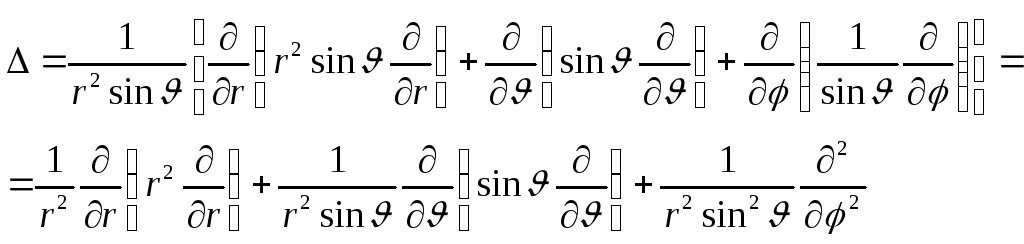
Приклад 3. Параболічні координати зв’язані з декартовими системою співвідношень

,,

Знайдемо оператор Лапласа в параболічних координатах.

Компоненти метричного тензора, як показують обчислення дорівнюють

, ,,,

Звідси

,,

а оператор Лапласа дорівнює

Виведемо ще іншу, еквівалентну /35.9/, формулу для оператора Лапласа. Приймаючи ми маємо

і остаточно

/35.11/

Познайомимось ще з ротором векторного поля в криволінійних координатах. Як ми показали в 30, різниця

-123-

є коваріантним антисиметричним тензором другого рангу, тобто псевдовектором. Власне цей псевдовектор, компоненти якого дорівнюють

, ,

є ротором векторного поля

/35.12/

Компоненти вектора R можна записати за допомогою символа e який зводиться так:

якщо два індекси однакові,

якщо i,j,k є парною перестановкою чисел 1,2,3,

якщо i,j,k є непарною перестановкою чисел 1,2,3.

Тоді

/35.13/

Дійсно, для i=1 ми маємо

Аналогічно одержуються вирази для R² і R³.

Те, що створюється ціною найбільших зусиль, повинно виглядати як таке, що створене швидко, майже без зусиль, з усією легкістю, наперекір правді.

Мікеланджело

36. Геодезичні лінії

Геодезичною лінією називається лінія найкоротшої віддалі в просторі криволінійних координат. В евклідовому просторі геодезичною є пряма лінія. На початку сфери такими лініями є великі круги.

Довжина лінії, що з’єднкє точки p₁ і p₂ дорівнює

, /36.1/

де p – довільний параметр.

-124-

Екстремум функціонала

визначається рівнянням Ейлера-Лагранжа

У нашому випадку

, ,

тоді

Варіаційний принцип запишеться

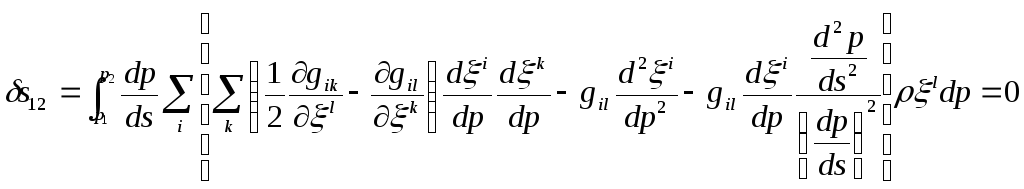
-125-

Симетризуємо першу групу доданків підінтегрального виразу

Рівняння геодезичних ліній одержується у вигляді

або, після перемноження на g^ls і сумування по l

/36.2/

Якщо за параметр прийняти дугу r=s, то ,і

/36.3/

У Декартові системі координат і /36.6/ переходить у рівняння прямої лінії

,

Модель є не що інше, як спосіб особливо виділити деякі властивості, відповідальне явище, що розглядається

В.Вейскопф

37.Інтегрувальність афінного зв’язку

Евклідовими називаються такі простори, в яких можна ввести Декартові координати. Простір, заданий метрикою

-126-

є евклідовим, якщо існує таке перетворення координат

що

де

Прикладом неевклідового простору є двохвимірна крива поверхня, яку можна розглядати як підпростір у трьох марному просторі. Геометричні властивості цього підпростору можна розглядати незалежно від простору, в який він вкладений.

Виберемо, наприклад, плоский лист /евклідову двохмірну поверхню/ і розграфимо його в клітку. Змінимо тепер зв’язок цієї поверхні з трьохмірним простором – згорнемо лист. Лінії на ньому і далі утворюють декартову систему. В обох випадках

,

Більше цього – лінії, що утворилися з прямих в результаті згортання і дальше залишаються лініяти найкоротшої віддалі. Таким чином, евклідовий характер простору залежить тільки від його метрики.

Розглянемо на площиніелементарну площадку, визначену точками

Далі розглянемо вектор Aⁿ і визначимо його зміну при обході контура ABCDA.

У декартовій системі ми зустрінемось зі звичайними похідними . В узагальнених координатахзвичайну похідну треба замінити на коваріантну

/37.1/

-127-

Зміна векторі Aⁿ на відрізках контура дорівнює:

1/ AB:

2/ BC:

3/ CD:

4/ DA:

Комбінуючи /2/ і /4/ знайдемо різницю змін в точках

Аналогічно для /3/ і /1/ маємо

а повна абсолютна зміна вектора Aⁿ вздовж контура ABCDA буде

/37.2/

Здавалось би, що цей вираз повинен дорівнювати нулеві. Однак, взагалі кажучи,

/37.3/

тобто результат коваріантного диференціювання залежить від порядку диференціювання.

Проаналізуємо це питання детальніше. Якщо ABCDA – прямокутник на площині /елемент плоского двохмірного простору/, то при паралельному перенесенні вектора Aⁿ вздовж контура його зміна дорівнюватиме нулеві

/37.4/

Нічого не зміниться, якщо замість декартових введемо криволінійні координати

/37.5/

Якщо двохмірний простір викривлений /наприклад, ABCDA – елемент поверхні сфери/, то при паралельному перенесенні вздовж контура перенесений вектор Aⁿ не збігається з вихідним і тоді

/37.6/

-128-

Якщо перенесений паралельно вектор A вздовж довільної кривої збігається з вихідним, афінний зв’язок називається інтегрувальним /рис.81а/. У цьому випадку діє закон паралельного перенесення

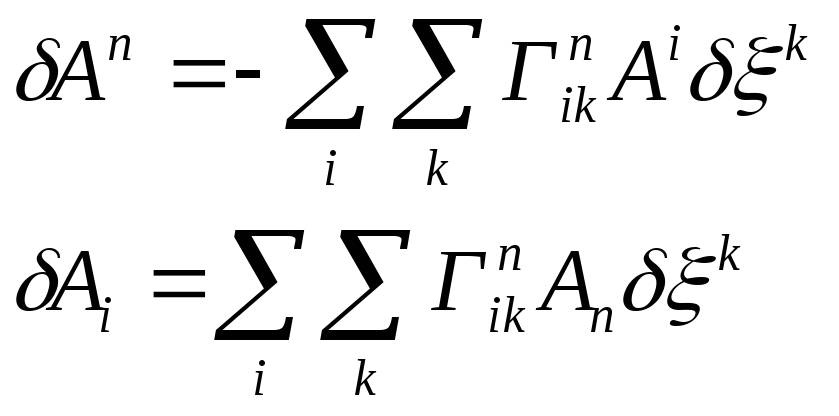
а для довільного замкненого контура С

/37.7/

У противному разі, коли перенесений паралельно вектор не збігається з вихідним, афінний зв’язок називається не інтегрувальним /рис.81б/ і тоді

/37.8/

Зрозуміло, що для плоских просторів /g_ik=const/ афінний зв’язок завжди інтегрувальний, навіть, якщо замість декартових чи косокутних координат користуються більш складними змінними.

Любов приходить і відходить. Тензорний аналіз вічний.

/З розмови старших людей/

38.Тензор кривизни Рімана-Крістоффеля

Якщо афінний зв’язок простору інтегрувальний, то рівняння паралельного перенесення можна розглядати як рівняння в частинних похідних для векторного поля.

/38.1/

/38.2/

-129-

Рівняння /38.1/ – перевизначенні: для визначення n компонент вектора маємо n² рівнянь /n – число вимірів простору/. Щоб система мала розв’язки, мусить задовольнятися ряд диференціальних тотожностей.

Візьмемо похідну по від /38.1/

Переставляючи індекси i,k, одержимо

і тому

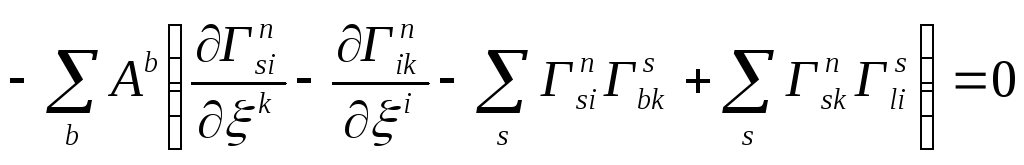
Вектор А довільний, Отже

/38.3/

- умова інтегрувальності афінного зв’язку.

Переконаємося, що для просторів з не інтегрувальним афінним зв’язком

Знайдемо різницю

За відомими правилами коваріантного диференціювання

-130-

Нам залишається підставити сюди вирази для

,

і, остаточно, ми маємо

Вираз для ми одержимо з останньої рівності, переставляючи індекси i,k. Легке бачити, що при підрахунках різниці

більшість доданків скорочується. Доданки, що не скорочуються підкреслені хвилястою лінією в остаточній формулі. Пере позначимо нарешті, індекс сумування в доданку

тоді

/38.4/

де

/38.5/

– тензор кривизни Рімана-Крістоффеля.

Перестановочні співвідношення для коваріантного диференціюван-

-131-

ня коваріантних векторів мають вигляд

/38.6/

що доводиться подібно, як /38.4/.

У метричному просторі тензор кривизни набуває вигляду

/38.7/

Всі великі правди на початку є богохульством.

Б.Шоу

39. Властивості тензора кривизни

I. Тензор кривизни антисиметричний стосовно індексів i,k

/39.1/

Ця властивість автоматично випливає з /38.5/ і не залежить від властивостей симетрії

Якщо афінний зв’язок симетричний то тензормає дальші властивості:

2. Сума компонент тензора кривизни, що отримується при циклічній перестановці перших трьох індексів, дорівнює нулеві

/39.2/

Доведення проводиться безпосереднім підрахунком за формулою /38.5/.

3. Виведеио т.зв. тотожності Б’янкі.

Від обох сторін рівності

візьмемо коваріантну похідну

Перепишемо цю рівність ще два рази, змінюючи циклічно індекси i,k,l

Додамо всі три рівності і згрупуємо доданки

/39.9/

-132-

Перетворимо вирази, що стоять у дужках. Позначимо

Згадаємо перестановочні співвідношення

і запишемо їх для коваріантного тензора другого рангу

Якщо , то

Підставимо ці вирази в /39.3/ і враховуємо /39.2/. Після скорочення одержимо тотожності Б’янкі

/39.4/

Введемо тепер коваріантний тензор кривизни в метричному просторі шляхом опускання контраваріантного індекса

/39.5/

Знайдемо формулу, яка дозволяє виразити R_iklm через символи Крістоффеля першого роду.

Використаємо допоміжну формулу

Перший доданок /38.7/ запишеться

і аналогічно другий

-133-

Тензор R_iklm можна тоді записати у вигляді

Замінимо тут символ Крістоффера другого роду символами першого роду

,

тоді R_iklm набуде вигляду

або, остаточно, перепозначуючи німі індекси r і s в третій групі доданків

Щоб знайти інший вираз для R_iklm розкриємо формули для [bi,m] і [lk,m]. Тоді

-134-

Підставимо ці вирази в /39.6/. Після скорочення одержимо

/39.7/

Звідси зразу видно, що R_iklm антисиметричний стосовно останніх двох індексів

/39.9/

Для коваріантного тензора справедлива і рівність /39.2/

/39.10/

Трагедія людства полягає в тому, що воно розв’язує проблеми Космосу, не розв’язавши ще земних проблем.

Дж.Стейнбек

40. Згортання тензора кривизни

З допомогою операції згортки тензора можна одержати тензори другого рангу

,,,/40.1/

Всі інші згортки дорівнюють нулеві завдяки /39.8/ - /39.10/.

Наприклад,

дорівнює нулеві як згортка антисиметричного тензора з симетричним.

Всі тензори /40.1/ рівні з точністю до знака. Наприклад,

-135-

завдяки рівності

Введемо позначення

/40.2/

/тензор Річчі/. Згортаючи цей тензор, отримаємо скалярну кривизну

/40.3/

Згідно з загальною формулою

ми маємо

/40.4/

Тензор R_kb симетричний. Симетрія останніх трьох доданків у /40.4/ очевидна, тому розглянемо перший доданок

Різниця є антисиметричним виразом відносноr і s його згортка з симетричним тензором дорівнює нулеві. Залишається

де g – детермінант, побудований з g_ik. Тому

а вираз цей симетричний відносно r,l. Таким чином

/40.5/

Виведемо тепер т.зв. згорнені тотожності В’янжі. Рівність

/ми чітко вказуємо точками місця, на які будемо піднімати або опускати індекси/ згорнемо по індексах i,n

-136-

тоді

Обидві сторони цієї рівності помножимо на g^ms і просумуємо по s. Відповідно доданки дорівнюють

Збираючи доданки одержимо

Згорнемо цю рівність по індексах k,m

отже,

Одержану рівність помножимо на g^bs і просумуємо по l

і остаточно

/40.6/

Вираз, що стоїть в дужці, звичайно позначають через G^bs

/тензор Ейнштейна/

-137-

/40.7/

Отже,

/40.8/

– коваріантна дивергенція тензора Ейнштейна дорівнює нулеві. Ця рівність і є записом згорнених тотожностей Б’янкі.

У релятивістській космології розглядаються більш загальний вираз для тензора Ейнштейна

/40.9/

де – стала величина /космологічна стала/. Очевидно, тензор /40.9/ також задовольняє згорнені тотожності Б’янкі, тому що коваріантна поідна від метричного тензора дорівнює нулеві.

Запишемо ще коваріантний і мішаний тензори Ейнштейна

/40.10/

/40.11/

при цьому

/40.12/

Тому тензори R_ik і g_ik симетричні, то і тензор G_ik є симетричним.

Метафізика: Шукання в абсолютно тамній кімнаті чорного кота, який знаходиться в іншому місці.

М.Метерлінк

41. Число незалежних компонент тензора кривизни

Доведемо, що число незалежних компонент тензора кривизни в мірному просторі визначається формулою

/41.1/

Розділимо компоненти R_iklm на три групи:

1. Компоненти, в яких різні лише два індекси: Перші і другі пари індексів повинні збігатися попарно, а два індекси одної пари збігатися не можуть, тому що

-138-

Кількість складових такого типу, тобто складових R_ikik /складові R_ikki відрізняються лише знаком/, дорівнює числові пар (i,k) при

Множник появився тому, що послідовністьi,k не має значення.

2. Компоненти, які мають три різні індекси: всі вони зводяться до вигляду R_iklm.

Індекс i набуває n значень. З решти n-1 значень треба вибрати пари різних значень для k і m. Це можна зробити способами, тому

.

3. У компонентах третьої групи вся чотири індекси різні (R_ikbm). Першу пару індексів можна вибрати способом. Залишаєтьсяn-2 чисел інших індексів, цю пару можна вибрати способами. Тому що послідовність обох пар не має значеннярезультат треба ще розділити на 2. Тому

Коефіцієнт ми поставили, враховуючи тотожність

Повне число алгебраїчно незалежних компонент дорівнює

тобто

У двохмірному просторі (n=2)

N=1

– один скаляр R повністю характеризує кривизну.

У трьохмірному просторі N=6 /стільки компонент має R_kl/.

В чотирьохмірному просторі

N=20

а число згорнених компонент дорівнює 10. Тому прикривизна простору повністю визначається згорненим тензором

-139-

Якщо хочеш бути щасливим три години – випий півлітри /кефіру/, якщо хочеш бути щасливим три дні – одружися, якщо хочеш бути щасливим три тижні – заколи порося і з’їж його, якщо хочеш бути щасливим все життя – вивчай тензорний аналіз.

/Підслухане/

42. Тензорний характер законів фізики

На початку згадаємо деякі факти, відомі з елементарної фізики.

Розглянемо рівняння

/42.1/

де A,B,C – якісь фізичні величини. Очевидно, що всі три величини мусять мати однакову розмірність. Наприклад А вимірюється в метрах, то таку ж розмірність порвинні мати і величини В, С. Інша справа, що в рівності

величини А, В, С можуть мати різну розмірність.

Звернемо увагу ще на одну властивість фізичних законів. Якщо закон задається рівнянням

А=В,

то величини А і В повинні мати однакову «тензорну розмірність». Ц означає, що якщо А є скаляром, то і величина В також є скаляром. Якщо А є вектором, то і В є вектором. Зрозуміло, що це правило поширюється і на тензори вищих рангів. У рівнянні

/42.2/

тензори T i U мусять бути тензорами одного і того ж рангу, число ко­– і контраваріантних індексів повинні бути відповідн однаковими. Лише у такому випадку можна сподіватися, що закон фізики буде справедливий в усіх системах координат.

Як приклад розглянемо закон Гука з механіки деформованого середовища

Тут – тензор напружень,– тензор деформацій,– коефіцієнти, що характеризують пружні властивості речовини,– об’ємна дилатація. Всі доданки мають однакову тензорну розмірність –– коваріантні симетричні тензори другого рангу.

Сформульований нами принцип має велику евристичну силу. Якщо

-140-

якийсь закон фіфзики справедливий в одній системі координат /чи в одному класі координатних систем/, то шляхом перетворення координат ми можемо знайти більш загальний закон, справедливий в усіх системах.

Проілюструємо це на прикладі з теоретичної механіки.

Як відомо, другий закон механіки

/42.3/

в справедливим лише в інерціальних системах координат. Нагадаємо, що інерціальною системою називається така система, в якій точка, на яку не діють жадні сили, рухається прямолінійно і рівномірно.

Розглянемо систему, що рухається прямолінійно і рівномірно стосовно інерціальної системи. Тоді

,

Компоненти вектора перетворюється за таким же законом, що й координати

.

Тому що

,

рівняння /42.3/ набуває вигляду

а звідси випливає, що

/42.4/

– другий закон механіки справедливий в усіх інерціальних системах координат.

Розглянемо випадок, коли початки системізбігаються //, але– системаобертається навколо точки. Тоді,, звідки

-141-

,

.

Рівняння /42.4/ набуде вигляду

Обидві сторони рівності помножимо на і просумуємоі

Враховуючи, що

,

і користуючись правилом підстановки індекса, ми одержимо

– другий закон механіки в неінерціальній системі .

Перетворимо другий доданок у правій частині /42.5/. Про диференціюємо по часі умову

одержимо

Звідси випливає, що

,

і тоді

Вираз

/42.6/

називають тензором кутової швидкості. Це антисиметричний тензор другого рангу, що має шість істотно різних складових

-142-

Рівняння (42.50) набувають вигляду

. (42.7)

Таким чином, в неінерціальній системі координат крім сили, на точку діють ще дві додаткові сили:

сила К, що має проекції

і називається силою Коріоліса,

сила , проекції якої дорівнюють

і яку називають відцентровою силою.

Легко переконатися, що вектори сили Коріоліса перпендикулярний до вектора швидкості точки стосовно рухомої системи. Для цього обчислимо скалярний добуток двох векторів

.

Одержаний вираз є подвійною згорткою симетричного тензора і антисиметричного тензора. Такий вираз дорівнює нулеві і тому.

У спеціальному випадку, коли осі іобох систем збігаються, а системарівномірно обертається навколо осі z з кутовою швидкістю

Коефіцієнти перетворення і їх похідні визначаються матрицями

тому

-143-

, ,,

а проекції Коріоліса на осі рухомої системи дорівнюють

,

, .

При перетворенні подібного типу потрібна особлива обережність. Відомо, наприклад, що теорема моментів для руху твердого тіла навколо рухомої точки

,

де – момент кількості руху тіла,– головний момент зовнішніх сил, справедлива лише в інерціальних системах. Щоб записати закон в будь-якій неінерціальній системі, треба врахувати, щоів аксіальними векторами, тобто псевдовекторами. Їх треба розглядати як антисиметричні тензориі. Рівняння (42.8) треба записати у вигляді

Дальше переходять від інерціальної системи до інерціальної системи, зв’язаної з твердим тілом. В результаті одержується відоме рівняння Ейлера для руху твердого тіла навколо нерухомої точки

У природі немає превілейованих систем координат (для простоти ми не розрізняємо поняття «система координат» від поняття «система відліку»). Всі інерціальні системи рівноправні з точки зору релятивістської механіки і електродинаміки. Неінерціальні системи також придатні до запису законів фізики. З другого боку, як ми бачили на прикладі другого закону механіки, один і той же закон записується, взагалі кажучи, по різному в різних системах координат. Тому перед фізиками стоїть принципово важлива задача: записати закони природи в такому вигляді, який був би одинаковий на всіх сиcтемах.. рівняння, вигляд яких не залежить від вибору сиcтеми координат, називається коваріантними, запис таких рівнянь – коваріантним.

-144-

Тензорні методи дозволяють записати закони природи в коваріантній – тензорній формі. Цю програму вдалося чітко реалізувати в усіх розділах теоретичної фізики, знайдено строгі правила узагальнення звичайних рівнянь на тензорні рівняння, які не змінюють свого вигляду при переході від однієї системи до іншої.

Наведемо приклад. Як відомо, багато законів фізики записуються у вигляді диференціальних рівнянь. Однак, звичайна похідна від тензора не має тензорної розмірності, не є тензором. Якщо рівняння має вигляд

(пор. (37.1.) і рівняння

вже є тензором.

Зміст

ВЕКТОРНИЙ АНАЛІЗ

1. Перетворення прямокутних координат точки

2. Перетворення компонент вектора при переході від одної прямокутної системи до іншої

3. Елементи вищої алгебри

4. Псевдовеличини

5. Вектор–функція скалярного аргумента

6. Скалярне і векторне поле. Градієнт скалярного поля

7. Похідна від вектора по напрямку

8. Потенціальне векторне поле. Лінійний інтеграл від вектора

9. Потік вектора через поверхню. Дивергенціал вектора

10. Теорема Остроградського–Гаусса

11. Рівняння Лапласа

12. Ротор вектора

13. Теорема Стокса

14. Деякі формули векторного аналізу

15. Соленоїдальні поля

ТЕНЗОРНИЙ АНАЛІЗ

16. Косокутні системи координат. Узагальнені проекції та узагальнені складові вектора. Дуальна система координат

17. Метричний тензор у косокутних координатах

18. Скалярний і векторний добуток двох векторів в косокутних координатах

19. Правила індексів

20. Диференціал операції в косокутних координатах

21. Перетворення координат і компонент вектора при переході від одної косокутної системи до іншої

22. Скаляри, вектори і тензори в косокутній системі координат

23. Приклади тензорів

24. Згортання тензорів

25. Деякі властивості симетричних тензорів другого рангу

26. Антисиметричні тензори другого рангу

27. Диференціальні операції над тензорами

28. Криволінійні координати

29. Метричний тензор в криволінійних координатах

30. Тензори в криволінійних просторах

31. Метричні простори

32. Задача про паралельне перенесення вектора

33. Символи Крістоффеля. Класифікація просторів

34. Коваріантне диференціювання

35. Диференціальні операції в метричних просторах

36. Геодизичні лінії

37. Інтегрувальність афінного зв’язку

38. Тензор кривизни Рімана–Крістоффеля

39. Властивості тензора кривизни

40. Згортання тензора кривизни

41. Число незалежних компонент тензора кривизни

Тензорний характер законів фізики