comp2009

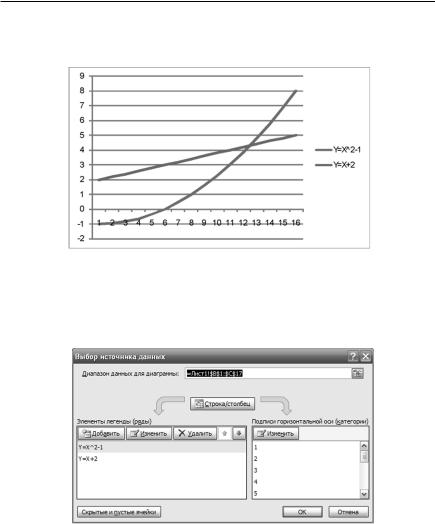
1.Практикум по курсу пользователя персонального компьютера "

2.Выделить диапазон ячеек В1:С5, перейти к вкладке Вставка/График, выбрать первый тип в первом ряду. На листе появится график вида рис. 1.24. Заметим, что он требует корректировки.

Рис. 1.24

3. Требуется выполнить настройку оси абсцисс. Выделить диаграмму, перейти к вкладке Конструктор/Выбрать данные. Вид диалога представлен на рис. 1.25.

Рис. 1.25

4. Изменить подписи горизонтальной оси (категории). Выделить ячейки А2:А17. Убедиться, что подписи оси абсцисс на диаграмме изменились в соответствии с заданными.

31

"Компьютерный практикум по информатике и программированию

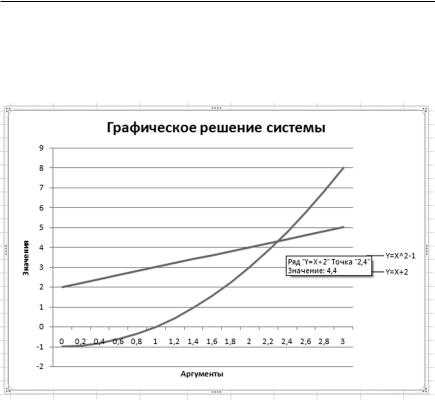
5.Установить Названия осей: для горизонтальной оси как Аргументы, вертикальной оси как Значения. Установить Название диаграммы

как Графической решение системы.

6.Определить значения x и y, наведя курсор на точку пересечения графиков, например, на рис. 1.26 эти значения, соответственно 2,4 и 4,4.

Рис. 1.26

Задание 2. Найти графическое решение системы уравнений по ва-

32

Задание 3. Построить пространственную диаграмму для поверх-

33

"Компьютерный практикум по информатике и программированию

2.На листе Microsoft Office Excel 2007 заполнить диапазон ячеек A2: A32 значениями от –3 до 3 с шагом 0,2 — эти значения будут значениями переменной x. Заполнить диапазон ячеек B1:V1 значениями от –2 до 2 с шагом 0,2 — эти значения будут значениями переменной y.

3.В ячейку В2 ввести формулу — решение уравнения относительно z

то есть =($A2^2/2 + B$1^2/3)/2.

4.Выполнить автозаполнение этой формулой диапазона ячеек В2: V32. Выделить этот диапазон с рассчитанными значениями.

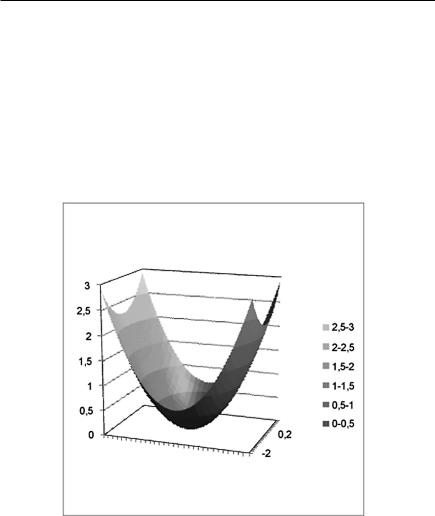
5.Выполнить Вставка/ Диаграмма/ Другие диаграммы/ Поверхность.

Выполнить настройку осей абсцисс и ординат диаграммы в диалоге Выбор источника данных. Вид поверхности показан на рис. 1.27.

Эллиптический параболоид

Рис. 1.27

Задание 4. Построить поверхности второго порядка, выбрав величины отрезков и шаг изменения по осям абсцисс и ординат и параметры самостоятельно, по вариантам.

34

1.Практикум по курсу пользователя персонального компьютера "

1.Действительный конус:

x2 y2

p− q = 2z.

1.4.4.Формулы массивов и матричные операторы

В Microsoft Office Excel 2007 имеется ряд встроенных формул, которые позволяют выполнять обработку данных в виде одномерных и двумерных массивов. Можно производить операции над массивами, которые существуют не только в виде диапазонов ячеек, но и которые находятся в памяти программы. Введенная формула будет являться формулой массива, если завершение ввода осуществляется клавишами Ctrl Shift Enter. После получения массива часть его формул изменить нельзя, изменение и удаление массива выполняется для всех его элементов одновременно.

Задание 1. С помощью формул массива составить календарь на один месяц года.

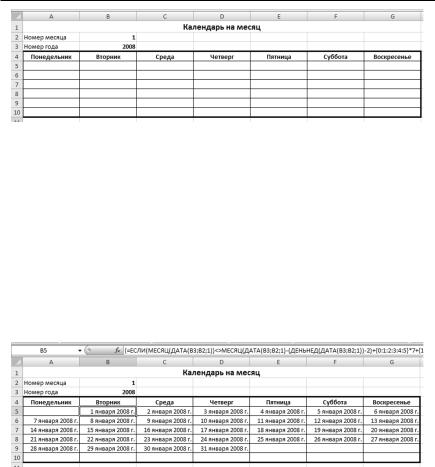
1. Подготовить лист с оформленной таблицей, как на рис. 1.28. Важно: номер месяца вводится в ячейку В2, номер года в ячейку B3.

35

" Компьютерный практикум по информатике и программированию

Рис. 1.28

2.Формула массива (расчет дней месяца по дням недели) вводится

вдиапазон ячеек A5:G10. Необходимо для этого диапазона установить формат ячеек Длинный формат даты.

3.Выделить диапазон ячеек A5:G10 и не снимая выделения перейти

встроку формул. Ввести формулу =ЕСЛИ(МЕСЯЦ(ДАТА(B3;B2;1))<>

МЕСЯЦ(ДАТА(B3;B2;1)-(ДЕНЬНЕД(ДАТА(B3;B2;1))-2)+{0:1:2:3:4:5}* 7+{1;2;3;4;5;6;7}-1);””;ДАТА(B3;B2;1)-(ДЕНЬНЕД(ДАТА(B3;B2;1))- 1)+{0:1:2:3:4:5}*7 + {1;2;3;4;5;6;7}) без пробелов и переносов по строкам

изавершить ввод Ctrl Shift Enter. Обратить внимание на то, что формула оказалась взятой в фигурные скобки — формула массива.

4.Окончательный вид календаря представлен на рис. 1.29.

Рис. 1.29

Задание 2. Подготовить календарь на год.

Задание 3. Найти решение системы линейных уравнений

2x + y + z = 6,

x + 2y – z = 3,3x – y + 2z = 4.

36

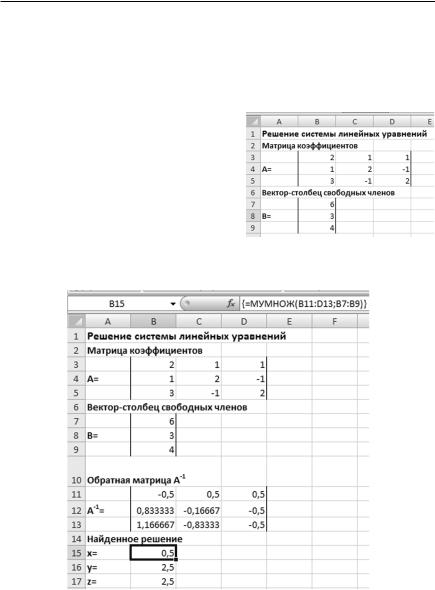
1.Практикум по курсу пользователя персонального компьютера "

1.Для нахождения решения требуется записать уравнение в матрич-

Рис. 1.31

37

" Компьютерный практикум по информатике и программированию

Задание 4. Найти решение системы линейных уравнений по матричному методу и методу Крамера, с проверкой возможности решения, в соответствии с вариантами:

1.4.5. Команда Подбор параметра

Задание 1. Определение точки безубыточности. Определить, какое количество товара нужно продать для покрытия всех издержек, связанных с его производством.

Задание 2. Определение приемлемой процентной ставки кредита. Пусть для постройки дома нужна ссуда 120 000 руб. Ваш бюджет допускает ежемесячные выплаты в размере 1000 руб. Пусть срок ссуды — 15 лет. Определить приемлемую фиксированную ставку кредита.

38

1. Практикум по курсу пользователя персонального компьютера "

Методика выполнения заданий

Команда Сервис/Подбор параметра позволяет по известному значению функции и её виду найти значение аргумента. Например, необходимо определить точку безубыточности, то есть определить, какое количество товара нужно продать для покрытия всех издержек, связанных с его производством. Иными словами должно выполняться равенство:

Общие расходы = Общие доходы,

где общие расходы = общие фиксированные расходы + расходы на произ-

водство единицы продукции × кол-во единиц.

Фиксированные расходы — расходы, не зависящие от объёма производства (например, расходы на монтаж какой-то технологической линии).

Общие доходы = Доход от продажи ед. × Количество проданных ед.

Решение подобных задач состоит из трёх этапов:

1)подготовительный (исходные данные занести в таблицу, ввести формулу для расчёта значения известного значения функции). Пример выполнения этого этапа представлен на рис. 1.32 (формула внесена в ячейку B10).

Рис. 1.32

2)выполнение команд Сервис/Подбор параметра и заполнение диалогового окна (рис. 1.33);

39

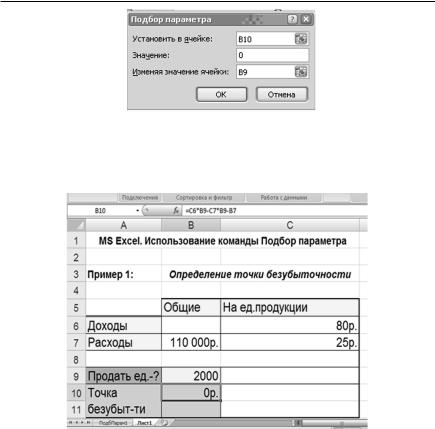
" Компьютерный практикум по информатике и программированию

Рис. 1.33

3)запуск программы на выполнение кнопкой ОК. Результат представлен на рис. 1.34.

Рис. 1.34

Варианты заданий

40