§4. ИССЛЕДОВАНИЕ ФУНКЦИЙ ПРИ ПОМОЩИ ПРОИЗВОДНЫХ

Производная применяется к исследованию функций и построению графиков функций.

4.1. Возрастание и убывание функций

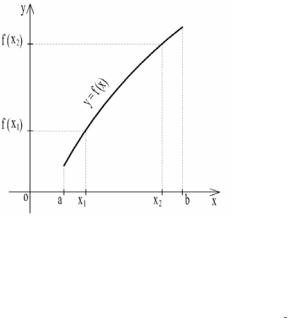
Определение. Функция y=f(x) называется возрастающей в интервале (a,b), если большему значению аргумента соответствует большее значение функции, т.е. f(x1) < f(x2) при х1 < x2 (x1,х2 (a,b)). На рисунке 12 приведен пример графика возрастающей функции.

Рис. 12

Функция y=f(x) называется убывающей в интервале (a,b), если большему значению аргумента соответствует меньшее значение функции, т.е. f(x1) > f(x2) при х1 < x2 (x1,х2 (a,b )). На

рис. 13 приведен пример графика убывающей функции.

39

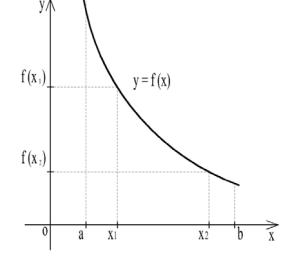
Рис. 13

Возрастающие и убывающие функции в интервале называются монотонными в этом интервале.

Теорема (достаточный признак возрастания и убывания функции на интервале).

интервале (а,b) возрастает. Аналогично доказывается вторая часть теоремы.

Пример 1. Доказать, что функция х3+2х при любом х возрастает.

40

Решение. Найдем производную:

у ' =(х3+2х) '=3х2+2>0.

Следовательно, функция возрастает при х (-∞;+∞).

4.2. Точки максимума и минимума функций

Рассмотрим функцию y=f(x), определенную в некоторой окрестности точки х0.

Определение. Точка х0 называется точкой максимума

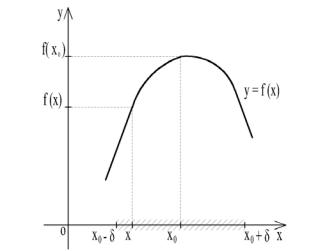
функции y=f(x), если существует такая окрестность точки х0, что для всех x ≠ x0 из этой окрестности выполняется неравенство

f(x) < f(x0), т.е. f(x0) – наибольшее среди значений функции в этой окрестности (рис.14).

Рис. 14

Точка х0 называется точкой минимума функции y=f(x), если существует такая окрестность точки х0, что для всех x ≠ x0

из этой окрестности выполняется неравенство f(x)> f(x0), т.е. f(x0) – наименьшее среди значений функции в этой окрестности

(рис.15).

41

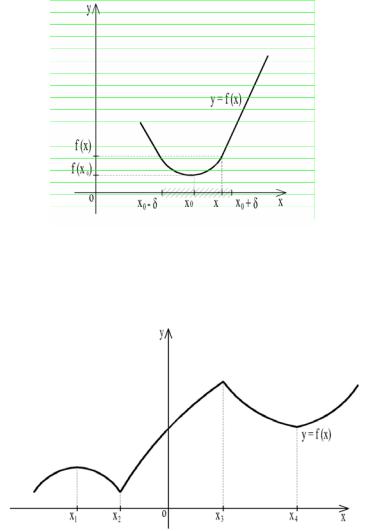
Рис. 15

Точки максимума и минимума функции называются точ-

ками экстремума этой функции.

Одна и та же функция может иметь несколько точек максимума и минимума с различными значениями функции в них.

Рис.16

Так у функции, график которой изображен на рисунке 16, х1 и х3 – точки максимума, х2 и х4 – точки минимума. Заметим, что значение функции в точке минимума х4 больше значения функции в точке максимума х1.

42

Теорема. Необходимый признак экстремума.

Пусть х0 – точка экстремума функции y= f(x). Тогда производная в этой точке равна нулю или не существует.

Доказательство. Пусть х0 – точка экстремума и пусть в этой точке существует производная. Так как на некотором интервале, содержащем х0, значение f(x0) – наибольшее или наименьшее среди значений, принимаемых на этом интервале, то по теореме Ферма f '(x0)=0.

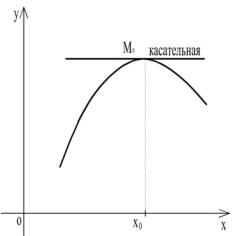
Геометрический смысл теоремы.

Если в точке экстремума х0 существует производная, то касательная, проведенная к графику функции в точке

М0 (х0, f(x0)), параллельна оси ОХ (cм. рис.17).

Рис. 17

Примером функции, не имеющей производной в точке экстремума, является функция у=|х|, которая в точке х=0 имеет минимум и не имеет производной (см. рис. 18).

Доказанное условие экстремума является необходимым, но не является достаточным.

Например, функция у=х3 в точке х=0 имеет производную у'=3х2=0, но не имеет в этой точке экстремума.

43

Рис. 18

Определение. Точка х0 называется критической для функции у=f(x), если функция определена в некоторой окрестности этой точки, а производная в этой точке равна нулю или не существует.

Вопрос о наличии экстремума в критических точках решается с помощью достаточных условий экстремума.

Теорема. Первый достаточный признак экстремума.

Пусть функция f(x) непрерывна в критической точке х0 и дифференцируема в некоторой окрестности точки х0 (кроме, быть может, самой точки х0). Тогда, если при переходе через точку х0 слева направо производная f '(x) меняет знак, то х0 является точкой экстремума.

Если при переходе через точку х0 слева направо производная меняет знак с плюса на минус, то х0 – точка максимума функции.

Если же при переходе через точку х0 слева направо производная меняет знак с минуса на плюс, то х0 – точка минимума.

Доказательство. Рассмотрим δ-окрестность точки х0. Пусть выполняются условия:

f '(x) > 0 V x (x0 – δ, x0) и f '(x) < 0 V x (x0, x0 + δ).

44

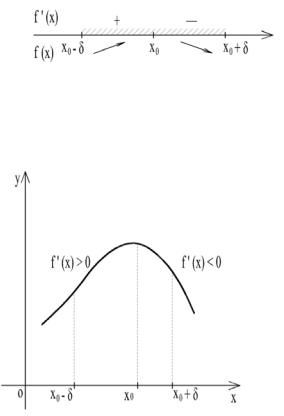
Тогда по достаточному признаку возрастания и убывания функция f(x) возрастает на интервале (х0 – δ, х0) и убывает на интервале (х0, х0 + δ) (рис.19). На рисунке стрелка, идущая вверх, означает возрастание функции на интервале, а стрелка, идущая вниз, означает убывание функции.

Рис. 19

Участок возрастания непрерывной функции сменился участком убывания, следовательно, х0 – точка максимума (рис. 20) .

Рис. 20

Аналогично теорема доказывается для случая, когда f´(x) < 0 V

x (x0 – δ, x0) и f´(x) > 0 V x (x0, x0 + δ) (рис. 21).

Замечание. Если при переходе через критическую точку производная не меняет знака, то экстремума в этой точке нет.

45

Рис. 21

Пример 2. Найти интервалы монотонности и точки экстремума функции y = x3 – 3x + 2.

Решение. Находим производную

y'=3x2 – 3=3(x2 – 1)=3(x – 1)(x + 1).

Находим критические точки. Производная равна нулю при х1= - 1 и х2= +1. Критические точки разбивают ось ОХ на три

интервала ( - ∞; - 1), (- 1; 1), (1; + ∞). Отметим на рисунке 22 знаки производной на каждом интервале.

Рис. 22

Следовательно, х1= -1 – точка максимума, f(-1)=4. Критическая точка х2=1 – точка минимума, f(1)=0. Функция возрастает на интервалах ( - ∞; - 1) и (1; + ∞); убывает на интервале ( -1; 1). График функции изображён на рис. 23.

46

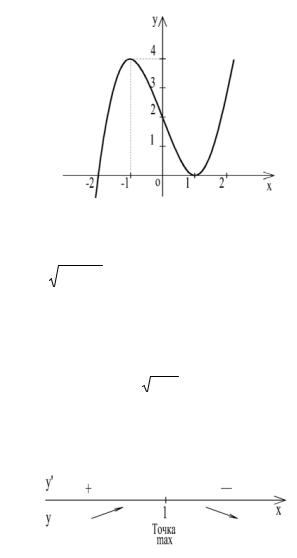
Рис. 23

Пример 3. Найти интервалы монотонности и точки экстремума функции

y = 1 – 3 (x −1)2 .

Решение. Функция определена при х ( - ∞; + ∞). Находим производную

Находим критические точки. Производная не существует при х = 1. Критическая точка х = 1 разбивает ось ОХ на два интервала ( - ∞; 1) и ( 1; + ∞). Отметим на рисунке 24 знаки производной на каждом интервале.

Рис. 24

Следовательно, х = 1 – точка максимума, f(1) = 1. Функция возрастает на интервале ( - ∞; 1); убывает на интервале (1; + ∞). График функции изображен на рис. 25.

47

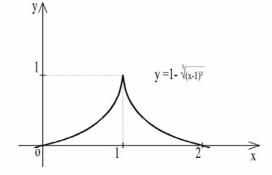
Рис. 25

Теорема. Второй достаточный признак экстремума.

Заметим, что f ′′(x0 ) = 0 может быть как в точках, где экстремума нет, так и в точках экстремума. Например, для функ-

следование нужно вести с помощью первого достаточного признака экстремума.

Исследуем вторым способом на экстремум функ-

f ′′(1) = 6 > 0, то x2 =1 - точка минимума функции.

48

Функцию y =1−3 (x −1)2 (пример 3) нельзя исследовать на экстремум по второму достаточному признаку, так как ее про-

изводная y′ = −33 x2−1 не существует в критической точке x =1.

4.3. Наибольшее и наименьшее значения функции на отрезке

Пусть функция y = f(x) непрерывна на отрезке [a,b], тогда она достигает своего наибольшего значения и своего наименьшего значения на этом отрезке. Эти значения функция может принять либо в точках экстремума, либо на концах отрезка [a,b].

Получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке [a,b]:

1)найти критические точки функции на отрезке [a,b];

2)вычислить значения функции во всех критических точках и на концах отрезка, т.е. в точках х = а и х = b;

3)из всех вычисленных значений функции выбрать наибольшее М и наименьшее m.

На рис. 26 наибольшее значение функции M = f(x0) достигается в точке максимума х0, а наименьшее значение m = f(b) достигается на правом конце отрезка.

Рис. 26

49

Пример 4. Найти наибольшее и наименьшее значения функции

f(x) = 3x4 – 4x3 – 2 на отрезке [-1;2].

Решение. Находим производную:

y' = (3x4 – 4x3 – 2)' = 12x3 – 12x2 = 12x2(x – 1).

Находим критические точки. Производная равна нулю при х1 = 0 и х2 = 1. Обе критических точки лежат на отрезке [-1;2]. Находим значения функции в критических точках и на концах отрезка:

f(0) = - 2, f(1) = 3 14 – 4 13 – 2 = -3, f(-1) = 3 (-1)4 – 4 (-1)3 – 2 = 5,

f(2) = 3 24 – 4 23 – 2 = 14.

Итак, наибольшее значение функции M = f(2) = 14, наименьшее значение функции m = f(1) = -3.

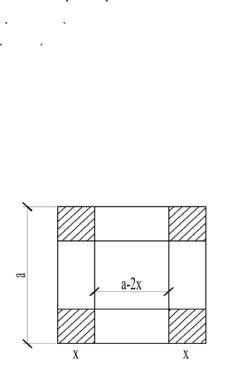
Пример 5. Из квадратного листа жести со стороной a , вырезая по углам равные квадраты и сгибая края, составляют открытую коробку. Как получить коробку наибольшей вместимости?

Решение.

Обозначим через x – сторону вырезаемых квадратов, через y – объём коробки (рис. 27).

Рис. 27

Тогда y = x ( a – 2 x )2. Задача свелась к нахождению наиболь-