
VMLA-Matzokin-2012 / 2012-лекции ЧА
.pdf
Мацокин А.М. “Численный анализ”. Конспект лекций.
Случай простого корня: p 1
Здесь мы докажем две теоремы, содержащие условия существования простого
корня x |
функции f (x) и сходимости к нему приближений метода Ньютона. |
|
|||||||||||||||||||||||||||||
Теорема 1. Если f (x) |
C1[a, b] выпукла вниз на отрезке [a, b] и |
|
|
|
|
|
|
||||||||||||||||||||||||
|
f (a) 0 , f (b) |
0 , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
уравнение f (x) |
|
0 имеет единственное |
|
решение x |
|
|
[a, b] ; |
|
||||||||||||||||||||||
|
приближения xn |
1 xn |
|
|
f (xn ) |
|
|
метода |
Ньютона |
|
при |
x0 x , |
|||||||||||||||||||
|
|
|
f (xn ) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
например, |
x0 |
a , строго возрастают и сходятся к этому корню. |
|
|||||||||||||||||||||||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
Существование решения x |
|
|
уравнения f (x) |
0 |
|||||||||||||||||||||
f (x0 ) |
|
|
|
|
|
следует из того, что |
|
f (x) |
|
|
C[a, b] |
|
принимает |
||||||||||||||||||
|
|
|
|
|
|
все значения между f (a) |
0 и f (b) |
0 . |
|
|
|
||||||||||||||||||||
f (x1) |
|
|
|
|
На картинке единственность корня очевидна, |
|
|||||||||||||||||||||||||
|
f (x2 ) |
|
|
|
|
но картинка не доказательство! |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Пусть |
|
x |
x |
|
|
|
|
− корни |
|
функции |
f (x) . |
Из |
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||
x1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определения |
|
|
выпуклости |
|
|
вниз |
|
|
и |
условия |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
f (b) |
0 следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Метод Ньютона для |
|
0 |
f (x |
) |
|
|
|
x |
b |
f (x |
) |
|
|
x |
|
|
x |
f (b) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
выпуклой вниз функции |
|
|
|
|
|
|
|
|
|
x |
b |
|
|
|
|
|
|
|
b |
|
x |
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
x |
|
|
f (b) |
0 |
|
|
|
x |
|
|
x |
|
|
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
b |
x |
|
|
|
|
|
b |
x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
и, значит, x |
|
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Теперь покажем, что последовательность {xn} метода Ньютона |
|||||||||||||||||||||||||||||||
определена и строго возрастает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Прежде всего, заметим, что на интервале [a, x ) |
функция |
|
f (x) |
0 |
и |
||||||||||||||||||||||||||
строго убывает, т.е. f (x) |
0 (докажите этот факт). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Тогда для xn |
[a, x ) мы можем вычислить |
xn |
1 |
|
|
xn |
|
|
f (xn ) |
|
xn |
и |
|||||||||||||||||||
|
|
|
|
f (xn ) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
xn 1 |
f (xn |
1) |
(докажите этот |
факт: |
|
график |
|
выпуклой |
вниз |
функции |
|||||||||||||||||||||
выше касательной в любой ее точке), т.е. xn |
1 |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Ограниченная |
строго |
возрастающая |
последовательность |
|
{xn} |
имеет |
|||||||||||||||||||||||||
x |
x и, |
переходя |
к |
пределу |
в |
равенстве |
f (xn )(xn |
1 |
|
xn ) |
f (xn ) , |
||||||||||||||||||||
убеждаемся, |
что |
он |
является |
|
корнем |
функции |
|
|
f (x) , |
|
а |
в |
силу |
||||||||||||||||||
единственности корня x |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
51
Мацокин А.М. “Численный анализ”. Конспект лекций.
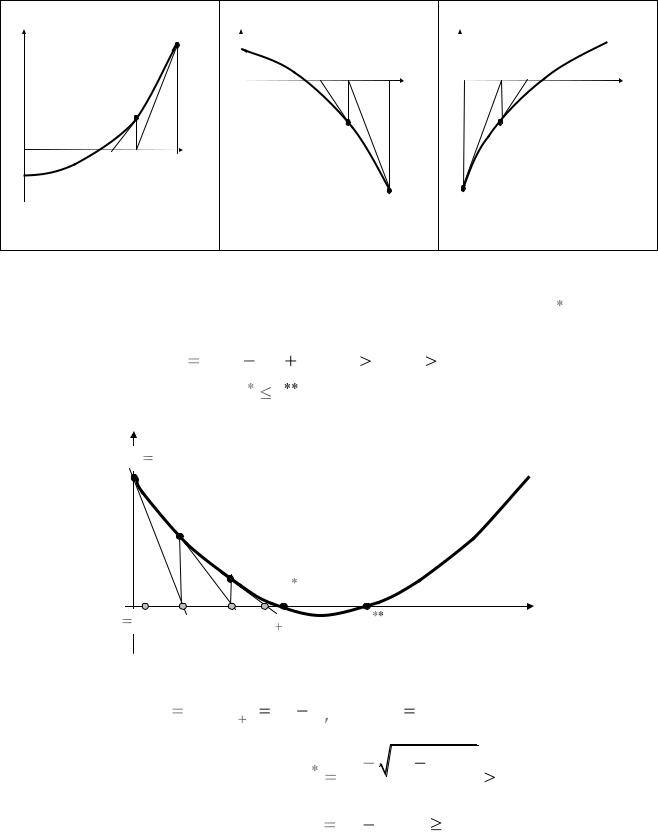
Замечание. Аналогичные теоремы можно сформулировать и доказать для случая вогнутых (выпуклых вверх) функций и изменения функции от отрицательных значений к положительным:
сформулируйте и докажите эти теоремы для нахождения корня функций методом Ньютона в соответствии с нижеприведенными картинками:
f (x) |
f (x) |
|
|
f (x) |
|
|
|
f (x0 ) |
|
|
|
|
|
|
x2 |
x1 |
x |
x1 |
x2 |
x |
|
|
|
|
|
f (x1) |
|
|
|
f (x1) |
f (x1) |
x2 x1 |
x |
|
|
|
|
|
f (x0 ) |
f (x0 ) |
Метод Ньютона для |
Метод Ньютона для |
Метод Ньютона для |
выпуклой вниз функции |
выпуклой вверх функции |
выпуклой вверх функции |
Прежде чем сформулировать и доказать вторую теорему мы рассмотрим
пример применения теоремы 1 для приближения меньшего корня t полинома второй степени
P(t) a |
2 |
t2 |
a t a |
0 |
, |
a |
2 |
0, a |
0 |
0 , |
(6) |
|
|
1 |
|
|
|
|
|
||||
с положительными корнями t |
t . |
|
|
|
|
|
|
|
|
||
P(t)
P(0) a0
|
|
|
t |
|
|
|
|
|
t |
0 t0 |
t1 |
tn |
tn 1 |
t |
Из теоремы 1 следует, что последовательность {tn } метода Ньютона |
|
||||||||
t |
0 |
0, t |
n 1 |
t |
n |
P(tn ) |
, n 0, 1, ..., |
(7) |
|
P (tn ) |
|||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
a |
a2 |
|
4a |
0 |
a |
2 |
|
||
строго возрастает и сходится к t |
1 |
|
1 |
|
|
|
0 , если (условие |
|||
|
2a2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
положительности корней полинома) D a2 |
4a |
0 |
a |
2 |
0 . |
|
|
|||
|
1 |
|
|
|
|
|
|
|
||
52

Мацокин А.М. “Численный анализ”. Конспект лекций.
Если (7) переписать в виде
t0 |
0, tn 1 |
tn |
P(tn ) |
|
tn |
a2 |
(tn |
t |
|
)(tn |
t |
) |
|
P (tn ) |
|
[a2 |
(tn |
t |
|
)(tn |
t |
)] |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|
|
|
(tn ) tn |
|
(tn |
t )(tn |
t |
) |
, n |
0, 1, ..., |
||||
|
|
|
2tn |
(t |
t |
) |
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
то погрешность метода удовлетворяет неравенствам
|
0 |
|
t |
tn |
1 |
|
|
|
|
|
(t |
) |
|
|
|
|
|
|
(tn ) |
( |
n )(t |
|
|
tn ) |
0.5 |
(t |
|
tn ) , |
(9) |
|||||||||||||||||
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
(t) |
|
[t |
|
(t |
|
|
t )(t |
t |
|
|
) |
] |
|
2(t |
|
|
t |
)(t |
t |
) |
|
|
1 |
|
|
t |
[0, t |
] , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)]2 |
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
2t |
|
(t |
|
t ) |
|
|
|
[2t |
|
|
(t |
|
|
t |
|
|
|
|
|
|
|
|||||||||||||||||||
т.е. скорость сходимости не хуже линейной (линейна при t |
t |
|
, почему?). |
|||||||||||||||||||||||||||||||||||||||||||
Если t |
t , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
(t) |
|
|
|
|
|
|
|
2(t |
|
|
|
t) |
|
|
|
|
(t |
|
t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
[2t |
|
|
|
(t |
t |
|
|
)] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
t |
|
|
|
t |
|
|
|
|
|
(t |
t) |
2 |
|
(t |
|
|
|
t) |
|
t |
[0, t |
] |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
[(t |
t) |
(t |
|
|
t)] |
|
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
t |
n 1 |
|
|
|
|
( |
|
|
n |
)(t |
|
t |
n |
) |
2 |
t |
|
|
|
n |
(t |
|
t |
n |
), |
n |
(t |
n |
, t |
) . |
|
|||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
( |
t |
|
|
n |
) |
|
|
|
t |
|
|
n |
|
t |
|
|
n |
|
0 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
d |
n |
|
t |
|
|
|
|
|
|
|
|
|
(t |
|
n )2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
n |
|
|
|
|
|
t |
|
tn |
|
|
|
t |
|
|
tn |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
n |
|
|
|
t |
|
|
tn |
|
|
|
t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
tn |
|
|
|
|
|
|
|
|
2 |
|
|
(t |
|
tn )2 |
|
|
|
|
|
|
|
|
|
|
(10) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. скорость сходимости метода Ньютона квадратичная. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Заметим, что в этом примере выполняются условия: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a2 |
|
1 |
|
max P (t) |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
P (0) |
|
|
|
a2 (t |
|
|
|
t |
|
) |
|
0, |
|
|
|
|
|
|
|
|
|
|
(11) |
|||||||||||||
|
|
|
|
|
|
|
|
a0 |
|
P(0) |
|
|
|
a2 |
(t |
|
t ) |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
53

Мацокин А.М. “Численный анализ”. Конспект лекций.
Теорема 2. Пусть f (x) |
C2[x0 |
|
|
, x0 |
], |
|
|
0, и |
|
||||||
|
a2 |
1 |
|
max |
| f |
(x) |, |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
||||||||||
|
|
|
|x |
x0| |
|
|
|
|
|
|
|
||||
|
a1 |
| f (x0 ) |, a1 |
0, |
|
|
|
|
||||||||
|
a0 |
| f (x0 ) |, a0 |
0, |
|
|
|
|
||||||||
а |
полином |
P(t) |
a |
2 |
t2 |
a t |
a |
0 |
имеет |
положительные корни |
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
t |
t и t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда f (x) имеет корень x |
[x0 |
, x0 |
], к которому сходится |
||||||||||||
последовательность {xn} метода Ньютона: |
|
||||||||||||||
|
x |
n 1 |
x |
n |
|
f (xn ) |
, |
n |
0, 1, ..., |
||||||
|
|
|
|||||||||||||
|
|
|
|
f (xn ) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и имеет место оценка
|
|
|
|
|
|
| xn |
x | t |
|
tn |
n 0, |
|
|
|
|
|
|
|
||||||||||||||
где {tn } − приближения по методу Ньютона (7) для корня t |
|||||||||||||||||||||||||||||||
полинома P(t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Прежде всего, напомним, что последовательность |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
t |
0 |
0, |
|
t |
n |
1 |
t |
n |
P(tn ) |
, |
n |
0, 1, ..., |
|
|
|
(7) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
P (tn ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
строго возрастает и сходиться к t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
При n |
0 по условию теоремы | f (x0 ) | |
a0 |
и | f (x0 ) | |
a1 |
0, |
значит |
|||||||||||||||||||||||||
x1 определен и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
| x |
|
x |
0 |
| |
|
|
| |
|
f (x0 ) |
| |
|
a0 |
|
|
|
P(0) |
t |
|
|
t |
0 |
t |
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
|
|
|
|
f (x0 ) |
|
a1 |
|
|
|
P (0) |
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Предположим, что для некоторого n |
|
|
1 доказано, что |
|
|
|
|
||||||||||||||||||||||||
|
|
| xk |
x0 | |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12) |
|||
|
|
| xk |
xk |
1 | |
|
|
tk |
|
|
tk |
1, |
k |
|
1, ..., n. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Покажем, что эти неравенства будут выполняться при k |
n |
1. |
|
||||||||||||||||||||||||||||
Для вычисления xn |
1 |
необходимо и достаточно показать, что f (xn ) |
0: |
||||||||||||||||||||||||||||
| f (xn ) | |
| f (x0 ) |
|
xn |
f |
(x) dx | |
|
| f (x0 ) | | |
xn |
f (x) dx | |
|
|
|
|||||||||||||||||||
|
x0 |
|
|
x0 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a1 |
2a2 |
| xn |
|
|
x0 | |
|
a1 |
|
2a2 |
|
( | xn |
xn |
|
|
1 | |
... |
| x1 |
x0 | ) |
|
|||||||||||
|
a1 |
2a2 |
( tn |
|
|
|
|
tn 1 ... |
|
t1 |
|
|
t0 ) |
a1 |
2a2 |
tn |
|
|
|
|
|||||||||||
|
P (tn ) |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значит xn |
1 существует. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
54

Мацокин А.М. “Численный анализ”. Конспект лекций.
Теперь нужно показать, что xn |
|
|
1 |
|
|
[x0 |
|
|
, x0 |
|
|
|
]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Сначала оценим | xn 1 |
|
|
|
|
xn |
|
| |
|
|
| |
|
f (xn ) |
|
|. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
f (xn ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Так как | f (xn ) | |
|
|
|
P (tn ) и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
| f (x |
n |
) | |
| f (x |
n 1 |
) f (x |
n 1 |
) (x |
n |
|
|
x |
n 1 |
) |
|
|
|
f ( |
|
n 1) |
(x |
n |
|
x |
n 1 |
)2 |
| |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
| |
f ( n 1) |
(x |
n |
|
|
|
x |
n 1 |
)2 | |
|
|
a |
2 |
(t |
n |
|
|
t |
n 1 |
)2 |
, |
|
|
n 1 |
[x |
n 1 |
, x |
n |
], |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(t |
n |
) |
P(t |
n 1 |
) |
|
|
P (t |
n 1 |
) |
(t |
n |
|
|
t |
n 1 |
) |
|
|
|
P (tn |
1) |
(t |
n |
t |
n 1 |
)2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
P (tn |
1) |
(t |
n |
|
|
|
|
t |
n |
1 |
)2 |
|
|
|
|
a |
2 |
|
|
(t |
n |
|
|
t |
n |
1 |
) |
2 , |
|
|
|
|
|
| f (x |
n |
) | P(t |
n |
) |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| xn 1 |
|
|
xn | |
|
|
| |
f (xn ) |
|
| |
|
|
|
|
P(tn ) |
|
|
|
|
tn 1 |
|
tn , |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f (xn ) |
|
|
|
|
|
P (tn ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
т.е. выполняется второе из предположений (12). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Теперь оценим xn |
1 |
|
x0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
| xn 1 |
|
x0 | |
|
|
|
|
| xn |
|
1 |
|
|
|
|
xn | ... |
| x1 |
|
x0 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(tn |
|
1 |
|
|
tn ) ... |
|
(t1 |
|
|
t0 ) |
|
|
tn 1 |
|
t |
|
|
|
, |
|
|
|
|
|
|||||||||||||||||||||||
т.е. выполняется и первое из предположений (12). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
И, наконец, из неравенств |
|
| xk |
|
1 |
|
|
|
|
xk | |
|
|
tk |
1 |
|
|
tk , |
справедливых для |
|||||||||||||||||||||||||||||||||||||||||||||||
любого |
|
целого |
|
|
|
k , |
|
|
|
|
следует |
|
|
|
|
|
фундаментальность |
|
по |
|
|
Коши |
||||||||||||||||||||||||||||||||||||||||||
последовательности {xn}, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
| xn |
m xn | |
|
| xn |
|
|
m |
|
|
xn |
|
|
|
m 1 | |
|
|
|
... |
|
|
| xn 1 |
|
xn | |
|
|
|
|
|
|
|
|
|
|
(13) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(tn |
|
|
|
|
|
|
|
tn m 1) ... |
(tn 1 |
|
|
tn ) |
|
|
tn m |
|
tn , |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
а сходящаяся последовательность {tn } фундаментальна по Коши. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
x |
|
|
|
|
[x0 |
|
|
, x0 |
|
|
|
], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (xn ) |
|
|
|
|
|
f (xn )(xn |
|
1 |
|
|
|
xn ) |
|
|
|
|
|
f (x |
|
) |
0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f (x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а переходя к пределу при m в (13), получим оценку сходимости:
| x xn | t tn |
n 0, что и требовалось доказать. |
55

Мацокин А.М. “Численный анализ”. Конспект лекций.
Метод Ньютона с параметром
Рассмотрим частный случай уравнения (1) на интервале [0, 1] f (x) xp 0, p 0,
т.е. x 0 – корень кратности p . Метод Ньютона в этом случае
xn |
1 |
xn |
xnp |
|
|
p xnp 1 |
|||||
|
|
|
|||
при p 0.5 не сходится, |
а |
при остальных |
|||
линейна.
Определим метод Ньютона с параметром:
p p 1 xn
p 1 скорость его сходимости
x |
n 1 |
x |
n |
p |
f (xn ) |
, n 0, 1, .... |
(14) |
|
f (xn ) |
||||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
Очевидно, что для нашего примера этот метод дает решение за одну итерацию при любом p 0 .
Метод Ньютона с параметром можно трактовать как метод простой итерации (последовательных приближений) решения уравнения
|
|
x |
|
|
(x) x |
p |
|
f (x) |
(1 |
p) |
x |
p |
(x) |
(15) |
|
|
|
|
|
f (x) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вместо уравнения x |
(x) |
x |
f (x) / f (x) . |
|
|
|
|
|
|||||||
Так как (x) |
|
p |
1 |
O(| x |
x |
|) , то |
(x) |
|
(1 |
p) |
p |
(x) |
O(| x x |) и |
||
|
|
|
|
|
|||||||||||
|
p |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn 1 |
|
x |
(xn ) |
|
(x |
) |
( |
n )(xn |
x |
) |
|
|||
|
|
|
|
|
O(| |
n |
|
x |)(xn |
x |
) |
O(| xn |
x |
| 2 ), |
||
т.е. метод Ньютона с параметром сходится при любой положительной
кратности p корня x |
функции f (x) |
и скорость его сходимости квадратичная |
||||||||||||||
(естественно при некоторых условиях на функцию f (x) ). |
|
|
||||||||||||||
Если |
кратность p |
корня x |
функции f (x) |
неизвестна, |
то, разрешая |
|||||||||||
(x) |
|
p 1 |
O(| x |
x |) относительно p , получим p |
1 |
O(| x x |) . |
||||||||||
|
|
|
|
|||||||||||||
|
p |
1 (x) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда итерационный процесс |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
n 1 |
x |
n |
|
|
1 |
|
f (xn ) |
, n |
0, 1, ..., |
(16) |
|
|
|
|
|
1 |
(xn ) f (xn ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
будет сходиться при достаточно близком к корню x |
приближении x0 , так как |
|||||
он является методом простой итерации для уравнения |
|
|
||||
x |
(x) (1 p) x p (x) |
(x) |
x |
(x) |
(17) |
|
|
|
|
||||
1 |
(x) |
|||||
|
|
|
||||
и (x ) 0.
56
Мацокин А.М. “Численный анализ”. Конспект лекций.
Литература
1.Бахвалов Н.С. Численные методы. - М.: Наука, 1975.
2.Березин И.С., Жидков Н.П. Методы вычислений. Ч.1. - М.: Наука, 1966.
3.Волков Е.А. Численные методы. - М.: Наука, 1987.
4.Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы.
Т.1. - М.: Наука, 1976.
5.Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989.
57
