
VMLA-Matzokin-2012 / 2012-лекции ЧА
.pdf
Мацокин А.М. “Численный анализ”. Конспект лекций. |
|
|||||||
Теорема 1 (принцип сжимающих отображений). |
|
|
|
|||||
Сжимающее |
отображение |
из |
полного |
метрического |
||||
пространства M в M имеет одну и только одну неподвижную |
||||||||
точку x M. |
|
|
|
|
|
|
|
|
Более того, последовательность метода простой итерации (метода |
||||||||
последовательных приближений) |
|
|
|
|||||
xn 1 |
(xn ), |
x0 M, n |
0, 1, ..., |
(6) |
||||
сходится к неподвижной точке и имеет место оценка |
|
|||||||
(x |
, xn ) |
|
(x1, x0 ) |
qn , |
n |
0. |
(7) |
|
|
|
|||||||
|
|
1 |
q |
|
|
|
||
Доказательство. |
|
|
|
|
|
|
|
|
Очевидно, что предел |
x |
(если он существует) |
последовательности (6) |
|||||
является неподвижной точкой отображения |
. Для существования предела |
|||||||
достаточно показать, что последовательность фундаментальна по Коши, так как пространство M полно.
Из определений последовательности и сжимающего отображения следует:
(xn m , xn ) ( (xn m 1), (xn 1) ) q ( xn m 1, xn 1 ) ...
qn ( xm , x0 ).
Из этого неравенства (и неравенства треугольника) следует, что
( xm , x0 ) |
|
( xm , xm 1 ) |
|
|
( xm 1, x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
qm 1 |
( x , x |
0 |
) |
|
( x |
m 1 |
, x |
0 |
) ... |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
qm 1 |
( x , x |
0 |
) |
|
qm |
2 |
|
( x , x |
0 |
) ... |
q0 |
( x , x |
0 |
) |
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||||
|
1 |
qm |
|
|
|
|
|
|
( x , x |
0 |
) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
( x1, x0 ) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
q |
|
|
1 |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и, значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xn m , xn ) qn |
( xm , x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
qn |
|
|
( x1, x0 ) |
|
|
|
n n |
|
|
|
m , |
|
|
|
|
(8) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. последовательность фундаментальна по Коши и xn |
x |
(x ) . |
|||||||||||||||||||||||||
Более того, переходя в неравенстве (8) |
к пределу при |
m |
, получим |
||||||||||||||||||||||||
оценку сходимости (7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Единственность неподвижной точки устанавливается элементарно: |
|
|
|||||||||||||||||||||||||
пусть x , x |
– два решения уравнения (5). Тогда |
|
|
|
|
|
|
||||||||||||||||||||
|
|
(x |
, x |
) |
( (x |
), |
(x |
|
) ) |
|
|
q |
(x |
, x |
) |
|
|
|
|||||||||
и, так как q |
1, то x |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
41

Мацокин А.М. “Численный анализ”. Конспект лекций.
Метод простой итерации
Вернемся к уравнению (1) на отрезке [a, b] и преобразуем его к виду
|
x |
(x) , |
(9) |
задав, например, |
(x) x (x) |
f (x) , где |
(x) − непрерывная, |
знакоопределенная на отрезке функция.
Рассмотрим для решения уравнения (9) метод простой итерации (6):
|
xn |
1 |
(xn ), x0 |
[a, b], |
n |
0, 1, ..., |
|
(10) |
|||||
Теорема 2. Если функция |
(x) |
C[a, b] непрерывна по Липшицу: |
|||||||||||
| |
(x) |
(y) | |
q | x |
y | |
|
x, y |
[a, b], |
q |
1 , |
(11) |
|||
и преобразует интервал [a, b] в [a, b] , т.е. |
|
|
|
||||||||||
|
a |
|
(x) |
b |
x |
[a, b] , |
|
|
|
|
(12) |
||
то уравнение (9) имеет единственное на [a, b] |
решение x , к |
||||||||||||
которому сходится последовательность {xn} метода простой |
|||||||||||||
итерации (10) при любом начальном приближении |
x0 [a, b] и |
||||||||||||
имеет место оценка |
|
|
|
|
|
|
|
|
|
|
|||
|
| x |
|
xn | |
|
| x1 |
x0 | |
qn . |
|
|
|
|
(13) |
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
q |
|
|
|
|
|
|
|
||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим |
метрическое |
пространство |
M |
[a, b] |
с |
расстоянием |
|||||||
(x, y) | x |
y |. Очевидно, что оно полно, а из условий (11) и (12) следует, |
||||||||||||
что (x) − |
сжимающее отображение из M в M и, |
значит, утверждения |
|||||||||||
этой теоремы являются прямым следствием теоремы 1. |
|
|
|||||||||||
Проверка условий теоремы 2 для конкретных функций |
(x) |
может вызвать |
|||||||||||
определенные затруднения. Действительно, условие (11) для непрерывно дифференцируемой функции означает ограниченность на интервале [a, b]
модуля ее первой производной постоянной Липшица q 1, а проверка условия
(12) заключается в поиске (или оценке) экстремальных значений самой функции, что может оказаться более сложной задачей по сравнению с решением уравнения (9).
Если константа Липшица q |
1 известна, то при достаточно удачном выборе |
||||||||
начального приближения |
x0 |
метода простой итерации удается избавиться от |
|||||||
проверки условия (12). |
|
|
|
|
|
|
|
|
|
Теорема 3. Если функция |
(x) |
C[a, b] |
непрерывна |
по |
|
Липшицу с |
|||
постоянной q |
1 и известно (хорошее) x0 |
[a, b] такое, что |
|||||||
[x0 |
|
, x0 |
] [a, b], |
| |
(x0 ) |
x0 |
| |
(14) |
|
|
|
|
1 |
q |
|
||||
|
|
|
|
|
|
|
|
||
(это условие можно проверить, если известна константа Липшица), |
|||||||||
то уравнение (9) имеет в [x0 , x0 |
] единственное решение x , |
||||||||
42

Мацокин А.М. “Численный анализ”. Конспект лекций.
к которому сходится последовательность метода простой итерации и имеет место оценка
|
|
|
|
|
|
|
|
|
| x |
|
xn | |
qn . |
|
|
|
|
|
|
|
|||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функция |
(x) отображает отрезок [x0 |
, x0 |
|
] в себя. Действительно, |
||||||||||||||||||||
|
|
|
|
| |
(x) |
x0 | |
| |
|
(x) |
|
(x0 ) | |
| |
(x0 ) |
x0 | |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
q | x |
|
x0 | |
(1 |
|
q) |
|
. |
|
|
|
|
||||
Следовательно, |
выполняются |
все |
условия |
теоремы |
2 |
на |
интервале |
|||||||||||||||||
[x0 |
|
, x0 |
|
], откуда следует сходимость и оценка сходимости метода |
||||||||||||||||||||
простой итерации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следующая теорема характеризует кратность корня функции f (x) |
x |
(x) . |
||||||||||||||||||||||
Теорема 4. Если функция |
(x) |
C[a, b] непрерывна по Липшицу: |
|
|
||||||||||||||||||||
|
|
|
| |
(x) |
|
(y) | |
q | x |
y | |
x, y |
[a, b], |
q |
1 , |
|
|
||||||||||
|
|
и преобразует интервал [a, b] в [a, b] , т.е. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
a |
|
(x) |
b |
|
x |
[a, b] , |
|
|
|
|
|
||||||
|
|
то функция f (x) |
x |
|
(x) |
имеет единственный на [a, b] корень |
||||||||||||||||||
|
|
x |
кратности единица. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Существование и единственность корня x |
функции |
f (x) |
на |
отрезке |
||||||||||||||||||||
[a, b] следует из теоремы 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Используя |
|
непрерывность |
по |
|
Липшицу |
функции |
|
(x) , |
получим |
|||||||||||||||
x |
|
[a, b] неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
| (x |
x ) |
f (x) | |
| |
|
|
(x) |
|
(x |
) | |
q | x |
x |
|. |
|
|
||||||
Но, т.к. | (x |
x |
) | |
|
| f (x) | |
| (x |
|
|
x ) |
f (x) | |
q | x |
x |
| , то |
|
|
||||||||||
(1 |
q) |
| (x |
|
x |
) | |
|
| f (x) | , и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.к. |
| f (x) | |
|
| (x |
x |
) | |
|
| (x |
x |
) |
|
f (x) | |
|
|
q | x |
x | , то |
|
|
|||||||
| f (x) | |
(1 |
q) |
| (x |
x |
) | , следовательно, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
1 |
q |
|
|
| f (x) | |
|
|
1 |
q |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
| x |
x |
| |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и, значит |
в |
представлении |
f (x) |
|
(x |
x ) |
g(x) непрерывная |
функция |
||||||||||||||||
g(x) знакоопределена, т.е. кратность корня x |
равна 1. |
|
|
|
|
|||||||||||||||||||
43

Мацокин А.М. “Численный анализ”. Конспект лекций.
Постройте и исследуйте сходимость метода простой итерации для решения
уравнения f (x) x2 |
|
a |
0 на интервале [1, a] . |
|
|
|
|||||||||||||||||
Решение. Преобразуем уравнение f (x) |
x2 |
a |
0 к виду |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x |
x |
|
|
(x2 |
a) |
|
(x) , |
|
|
|
|
|
|
||||
где постоянную |
надлежит выбрать из условий: |
|
|
|
|||||||||||||||||||
|
|
a) |
1 |
|
(x) |
x |
|
(x2 |
|
a) |
|
a |
|
x |
[1, a], |
|
|
||||||
|
|
b) |
| (x) | |
| 1 |
2 |
x | |
|
q |
1 |
|
x |
[1, a]. |
|
|
|||||||||
Начнем с условия b). Так как минимальное и максимальное значения |
|||||||||||||||||||||||
линейной функции достигаются на концах интервала [1, a] : |
|
||||||||||||||||||||||
|
|
max |
| |
|
(x) | |
max {| 1 |
2 |
|, | 1 |
2 |
a |} |
|
q( |
) . |
|
|
||||||||
|
|
x [1, a] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
То для того, чтобы q( |
) |
1, необходимо и достаточно выбрать |
из |
||||||||||||||||||||
условий: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
1 |
2 |
|
1, |
|
|
|
1 |
|
|
|
0, |
|
|
(0, 1 / a). |
|
|||||||
|
1 1 2 a 1, |
|
|
|
1/ a |
|
|
0, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Замечание. |
Минимум |
коэффициента |
q( |
) |
на |
интервале (0, a |
1) |
||||||||||||||||
достигается |
при |
|
|
opt |
|
1/ (1 |
a) |
и |
q( |
opt ) |
(a |
1) / (a |
1) . |
||||||||||
Докажите эти формулы (вспомните курс вычислительных методов |
|||||||||||||||||||||||
линейной |
|
алгебры: |
оптимизация |
|
метода |
простой |
итерации |
||||||||||||||||
xk 1 |
xk |
|
(Axk |
b) для решения системы Ax |
b ). |
|
|
||||||||||||||||
Теперь проверим условие a) при |
|
|
opt |
1/ (1 |
a) . Минимальное и |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
максимальное значения функции |
(x) достигаются либо при x |
1, |
|||||||||||||||||||||
либо в корне x |
1/ (2 |
|
opt ) |
(a |
1) / 2 |
(1, a) её производной, либо |
|||||||||||||||||
при x |
a : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a / (a |
1); |
|
|
|
|
|||
|
min [x |
|
(x2 |
a)] |
|
min |
|
(a |
1)2 |
4a |
; |
1, |
|
|
|||||||||
opt |
|
|
|
4(a |
|
|
|
||||||||||||||||
|
x |
[1, a] |
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a / (a |
1) |
|
|
|
|
|||
так как неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2a |
a |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(a |
1)2 |
|
4a |
1 |
(a |
1)2 |
4a |
|
4(a |
1) |
a2 |
2a |
3; |
|
||||||||
|
4(a |
1) |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
справедливы при a |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
44

Мацокин А.М. “Численный анализ”. Конспект лекций.
|
|
|
|
далее, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a / (a |
|
1); |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
max [x |
|
(x2 |
|
a)] |
max |
(a |
1)2 |
|
|
4a |
; |
|
|
a |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
opt |
|
4(a |
|
1) |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
x |
[1, a] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a / (a |
1) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
так как неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2a |
a(a |
1) |
|
a2 |
a |
2a, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
(a |
1)2 |
|
4a |
a |
(a |
1)2 |
4a |
4a(a |
1) |
|
|
|
|
3a2 |
2a |
|
1 |
0; |
|
|
|
||||||||||||
|
|
|
|
|
4(a |
1) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
справедливы при a |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Итак, |
при |
1/ (a |
|
1) отображение |
(x) : [1, a] |
|
[1, a] |
является |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
сжимающим с q |
(a |
1) / (a |
1) , к его неподвижной точке x |
|
a |
|||||||||||||||||||||||||||
|
|
|
|
сходится последовательность приближений метода простой |
||||||||||||||||||||||||||||||||
|
|
|
|
итерации: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
xn 1 |
xn |
(x2n |
a) / (a |
1), |
|
n |
0, 1, ..., |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
при любом начальном приближении x0 |
[1, a], |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
а для погрешности x |
xn справедлива оценка |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
| x |
xn | |
| x1 |
x0 | |
q |
n |
| x1 |
x0 | (a 1) |
|
(1 |
|
|
2 |
|
) |
n |
. |
|
|
|
|
||||||||||||
|
|
|
|
1 |
q |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
Метод Эйткена ускорения сходимости метода простой итерации |
|
|
|
|
||||||||||||||||||||||||||||||||
Пусть |
для |
функции |
(x) |
C2[a, b] выполняются |
условия |
теоремы 2, |
т.е. |
|||||||||||||||||||||||||||||
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(15) |
||||
имеет единственное решение x |
[a, b], к которому сходятся приближения |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
xn 1 |
|
(xn ), |
x0 |
[a, b], |
n |
|
0, 1, .... |
|
|
|
|
|
|
(16) |
||||||||||||||
Тогда, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
xn 1 |
|
(xn ) |
|
(x ) |
|
(x ) (xn |
x ) |
|
( |
n ) |
(xn |
|
x ) |
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
(17) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
|
(x ) |
(xn |
x |
) |
|
n , |
|
|
|
n |
|
O(| xn |
|
|
x | 2 ), |
|
|
|
|
|||||||||||
то |
для |
погрешности |
метода |
простой |
итерации |
|
имеем |
|
|
соотношение |
||||||||||||||||||||||||||
| xn 1 |
x |
| |
| |
(x ) | |
| (xn |
x ) | , т.е. за одну итерацию она уменьшается в |
||||||||||||||||||||||||||||||
| |
(x |
) | |
|
1 |
раз, |
если |
(x |
) |
0. Говорят, что метод простой итерации имеет |
|||||||||||||||||||||||||||
линейную скорость сходимости (при |
|
(x ) |
0 она была бы квадратичной). |
|||||||||||||||||||||||||||||||||
45

|
|
|
|
Мацокин А.М. “Численный анализ”. Конспект лекций. |
|
|
||||||||||||||||||||||
Предположим, |
|
что |
|
|
(x ) 0, и рассмотрим три последовательных |
|||||||||||||||||||||||
приближения xn , xn 1 |
и xn 2 . Согласно (17), они связаны следующими |
|||||||||||||||||||||||||||
соотношениями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
xn 1 |
x |
|
|
|
(x ) (xn |
|
|
|
x ) |
|
n , |
|
|
|
|
|
(18) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn 2 |
x |
|
|
|
(x ) (xn 1 |
x ) |
|
n 1. |
|
|
|
|
|
|||||||||||
Вычитая из второго равенства первое, получим |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
xn 2 |
xn 1 |
(x ) (xn 1 |
xn ) [ n 1 |
n ] |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
(x ) |
|
|
xn 2 |
|
xn 1 |
|
|
, |
|
|
|
n 1 |
n |
. |
|
(19) |
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xn 1 |
|
xn |
|
|
|
xn 1 |
xn |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Заменяя производную |
|
(x |
) в первом равенстве по формуле (19), получим |
|||||||||||||||||||||||||
x |
n |
1 |
x |
( |
xn 2 |
|
xn 1 |
n |
) (x |
n |
x ) |
n |
|
|
|
|
|
|
||||||||||
xn 1 |
xn |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
(1 |
|
xn |
2 |
xn |
1 |
) |
x |
|
xn |
2 |
|
xn |
1 |
x |
n |
[ |
n |
n |
(x |
n |
x )], |
||||
|
|
|
|
xn |
|
|
|
xn |
|
|
xn |
|||||||||||||||||
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
n
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
xn |
|
|
x |
|
|
( n 1 |
n ) , |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xn 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
xn 1 |
xn |
|
|
xn |
1 |
|
|
|
xn 2 |
|
xn 1 |
|
xn |
n , |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
xn |
2xn 1 |
|
|
|
|
xn |
2xn 1 |
|
xn 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
xn 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
xn |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
xn 1 |
xn |
|
|
|
|
n |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
2xn 1 |
xn 2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
xn |
1 |
|
xn |
|
|
|
[ |
|
|
n |
|
|
xn |
x |
|
( n |
1 |
|
|
|
n )]. |
|||||||||||
|
|
|
|
|
|
|
xn |
2xn 1 |
|
|
|
|
|
|
|
|
|
xn 1 |
xn |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
xn 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Проанализируем коэффициенты при xn |
1 и xn |
в (20): |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
xn 1 |
xn |
|
|
(1 |
|
xn 2 |
|
xn 1 |
) 1 |
|
|
|
(1 |
|
|
(xn 1) |
(xn ) |
) 1 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
xn 2xn 1 |
xn 2 |
|
|
xn 1 |
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
xn 1 |
xn |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
(1 |
|
|
( n ) (xn 1 |
|
xn ) |
) 1 n |
|
|
|
|
1 |
|
|
|
, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xn 1 |
|
xn |
|
|
|
|
|
|
|
|
|
1 |
(x ) |
|
|
|||||||||||||
|
|
|
|
|
|
xn 2 |
xn 1 |
|
|
|
|
|
|
(xn 2 |
xn 1) / (xn 1 |
|
xn ) |
|
|
||||||||||||||||||||||
|
|
|
|
|
xn |
|
2xn 1 |
xn 2 |
1 (xn 2 |
|
|
xn 1) / (xn 1 |
|
|
xn ) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
n ) |
|
|
n |
|
|
|
|
(x ) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
( |
n ) |
1 |
(x |
) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
(20)
(21)
(22)
46

Мацокин А.М. “Численный анализ”. Конспект лекций.
Так как константа |
|
(x |
) |
0 и | |
(x |
) | |
|
|
q 1, то эти коэффициенты являются |
||||||||||||||||||||||||||||
величинами порядка O(1) в некоторой (малой) окрестности неподвижной точки |
|||||||||||||||||||||||||||||||||||||
x и “линейная” комбинация |
xn 2 |
приближений |
xn |
1 |
|
и xn |
метода простой |
||||||||||||||||||||||||||||||
итерации имеет своим пределом x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
xn 1 |
xn |
|
|
|
|
|
|
|
|
|
|
|
xn 2 |
xn 1 |
|
|
|
|
|
|
|
n |
|||||||||||
xn |
2 |
|
|
|
|
|
xn |
1 |
|
|
|
|
|
|
|
|
|
|
|
xn |
|
||||||||||||||||
|
xn |
2xn 1 |
xn 2 |
|
|
|
|
|
|
xn |
|
2xn 1 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xn 2 |
(23) |
||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
x , |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
(x |
) |
|
|
1 |
|
|
(x |
) |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
а также оценку ошибки приближения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
n |
xn 2 |
x |
|
|
|
|
|
xn |
1 |
xn |
|
|
|
|
|
|
[ n |
|
|
xn |
x |
|
|
|
( n 1 |
n )] |
|||||||||||
|
|
xn |
2xn |
|
xn |
|
|
|
|
|
xn |
|
|
xn |
|||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
1 |
|
|
|
|
(24) |
|||||||||||||||||||
|
O((xn |
x |
)2 ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) первый множитель в правой части |
|
[1 |
|
|
|
(x |
)] 1 |
|
|
O(1) , |
|||||||||||||||||||||||||||
2) |
n |
|
O((xn |
x )2 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3) |
n 1 |
|
n |
O((xn |
x )2 |
|
(xn 1 |
x )2 ) |
|
|
|
O((xn |
x )2 ) , |
||||||||||||||||||||||||
4) множитель перед разностью |
n 1 |
n |
также |
O(1) : |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
xn |
x |
|
|
|
|
|
|
|
xn |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
xn 1 |
xn |
[x |
|
|
(x ) (xn |
x ) |
|
|
|
n ] xn |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
[ |
(x |
) |
|
1] (xn |
x |
) |
|
O((xn |
|
x |
)2 ) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
O(1). |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ (x ) 1] O(xn |
x |
) |
|
|
|
|
(x |
) |
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Обычно xn |
|
2 записывают в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
xn |
2 |
xn |
2 |
|
|
|
(xn |
2 |
|
xn 1)2 |
|
|
|
|
|
|
|
(25) |
||||||||||||
|
|
|
|
|
|
|
|
|
xn |
2xn 1 |
xn 2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
и называют методом Эйткена ускорения простой итерации по её трем последовательным приближениям:
xn , xn 1 |
(xn ), xn 2 |
(xn 1) |
|
[ (xn )], |
|
||||
Замечание. Метод Эйткена ускорения простой |
итерации xn 1 |
(xn ) |
|||||||
решения уравнения x |
|
(x) можно переписать в виде |
|
||||||
xn 2 |
[ (xn )] |
( |
[ |
(xn )] |
(xn ))2 |
|
(xn ) . |
|
|
|
xn |
|
(xn ) |
|
|
|
|||
|
|
|
2 |
[ (xn )] |
|
||||
47
Мацокин А.М. “Численный анализ”. Конспект лекций.
Проверьте, что (x ) |
x и |
(x ) 0. |
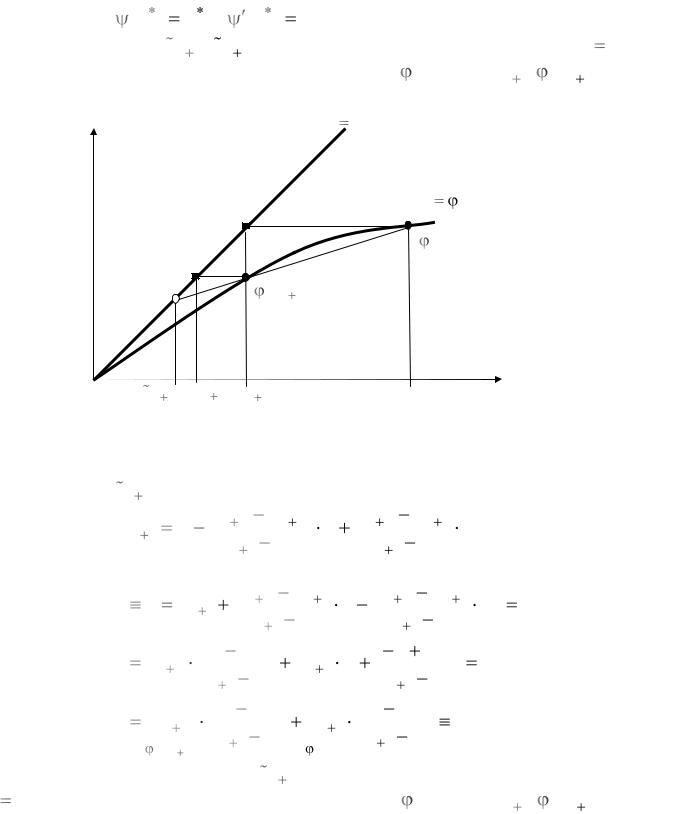
Докажем, что точка (xn |
2 , xn |
2 ) является точкой пересечения прямой y x |
и прямой, проходящей через точки (xn , (xn )) и (xn 1, (xn 1)) .
Y |
y x |
|
y (x)
(xn )
(xn 1)
xn 2 xn 2 xn 1 |
X |
xn |
Геометрическая интерпретация метода простой итерации и его ускорения методом Эйткена.
Действительно, xn |
2 мы находили, решая уравнение |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
x |
n |
1 |
|
(1 |
|
|
|
xn 2 |
xn 1 |
) x |
|
xn 2 |
xn 1 |
x |
n |
, |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
xn 1 |
xn |
|
|
|
|
|
|
xn |
|
|
xn |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
которое преобразуется к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y(x) |
|
x |
|
x |
n |
1 |
xn |
2 |
|
xn |
1 |
|
x |
|
xn |
2 |
xn |
1 |
|
|
x |
n |
|||||||||||
|
|
xn |
|
|
|
|
|
|
xn |
|
|
xn |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
|
|
x |
n |
2 |
|
|
|
|
x |
xn |
|
|
|
x |
n |
1 |
(1 |
|
|
x |
xn |
) |
|
|
|
|
|
||||||
|
|
|
|
xn 1 |
xn |
|
|
xn |
|
xn |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
xn |
2 |
|
|
|
|
x |
xn |
|
|
|
xn |
1 |
x |
xn |
|
|
|
L(x) |
|||||||||||||
|
|
|
|
|
|
xn |
1 |
xn |
|
|
|
xn |
1 |
xn |
|||||||||||||||||||
|
|
(xn |
1 ) |
|
|
|
|
|
|
(xn ) |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и, следовательно, его |
решение xn |
2 |
|
|
является |
точкой |
пересечения прямой |
||||||||||||||||||||||||||
y x и прямой L(x) , проходящей через точки (xn , |
(xn )) и |
|
(xn 1, (xn 1)) . |
||||||||||||||||||||||||||||||
48
Мацокин А.М. “Численный анализ”. Конспект лекций.
Лекция 6. Метод Ньютона
Пусть функция f (x) C1[a, b] и требуется решить уравнение |
|
f (x) 0 , |
(1) |
Идея метода Ньютона чрезвычайно проста: если xn − приближение к корню
x , то функция f (x) заменяется |
интерполяционным полиномом первой |
степени по ее значению f (xn ) и значению ее первой производной f (xn ) : |
|
f (x) f (xn ) |
f (xn ) (x xn ) , |
а корень этого полинома объявляется следующим приближением:
x |
n 1 |
x |
n |
f (xn ) |
, x |
0 |
[a, b], n 0, 1, ... . |
(2) |
|
||||||||
|
|
f (xn ) |
|
|
||||
|
|
|
|
|
|
|
||
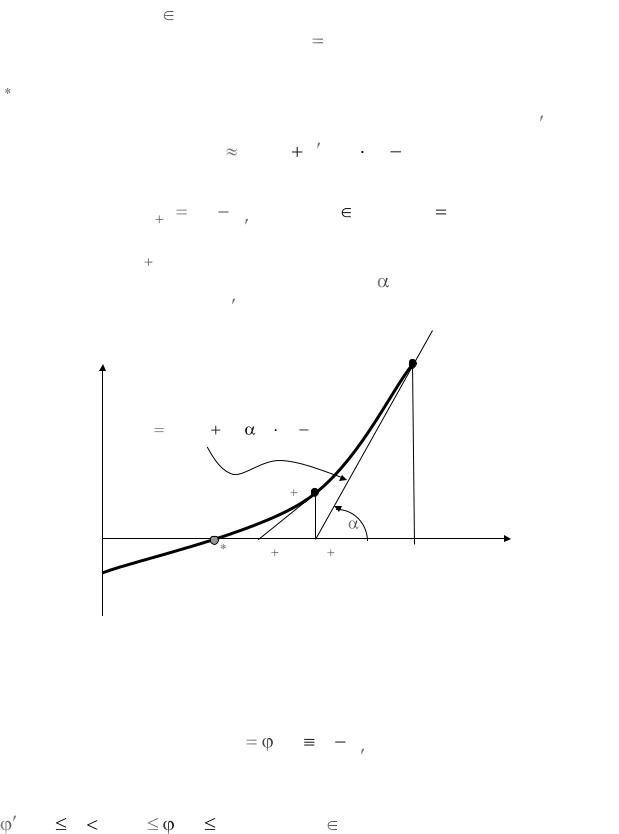
Докажите, что xn 1 является точкой пересечения прямой, проходящей через
точку (xn , f (xn )) и тангенсом угла |
n между прямой и осью |
||||||||||
абсцисс равным f (xn ) . |
|
|
|
|
|
|
|||||
y |
|
|
|
|
|
|
|
f (xn ) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y(x) f (xn ) |
tg( |
n ) |
(x |
xn ) |
|
|
||||
|
|
|
|
|
f (xn |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
x |
|
|
|
|
|
xn |
|
xn 1 |
||||
|
|
|
x |
2 |
xn |
||||||
|
|
f (x) |
|
||||||||
Геометрическая интерпретация метода Ньютона.
Очевидно, что метод Ньютона (2) решения уравнения (1) совпадает с методом простой итерации решения эквивалентного уравнения
x |
(x) x |
f (x) |
(3) |
|
|
||||
f (x) |
||||
|
|
|
и все результаты предыдущей лекции можно применить для исследования
сходимости |
метода, |
в |
основном теорему 5.2, где требуется, чтобы |
| (x) | q |
1 и a |
(x) |
b для всех x [a, b]. |
49

Мацокин А.М. “Численный анализ”. Конспект лекций.
Пусть x [a, b] − изолированный корень кратности p |
|
|
|
0 функции f (x) : |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
(x |
|
x )p g(x) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||||
где функция g(x) |
C2[a,b] знакоопределена в некоторой окрестности корня. |
|||||||||||||||||||||||||||||||||||||||
Тогда, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
x |
|
|
|
|
|
|
|
|
|
|
(x |
x |
)p g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
p(x |
|
|
x )p 1g(x) |
|
(x |
|
x |
)p g (x) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
x |
|
|
|
|
(x |
|
x |
|
)g(x) |
|
|
|
|
( |
x |
|
|
x |
|
|
|
x |
|
|
) |
|
|
|
|
|
||||||||
|
|
|
pg(x) |
(x |
|
|
|
x |
)g (x) |
|
|
|
|
|
p |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x |
|
x |
x |
|
|
|
|
|
|
|
|
|
g (x) |
|
|
|
|
|
|
(x |
|
|
x |
)2 , |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
p |
|
|
|
|
|
p[pg(x) |
|
(x |
|
x |
)g (x)] |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
|
|
p |
1 |
|
O(| x |
x |) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и приближения |
xn |
метода Ньютона |
(2) |
к |
корню |
x |
функции |
f (x) |
||||||||||||||||||||||||||||||||
удовлетворяют соотношениям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
xn 1 |
|
x |
|
|
|
(xn ) |
(x |
|
) |
|
|
( |
n )(xn |
|
|
|
x |
|
) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
p |
1 |
(xn |
x |
) |
|
O(| xn |
|
x |
|
| 2 ). |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из этого соотношения можно сделать следующие предположения: |
|
|
|
|||||||||||||||||||||||||||||||||||||
метод Ньютона не сходится, если p |
0.5, так как | |
p |
|
1 |
| |
1; |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||
метод Ньютона сходится, если p |
|
0.5, так как | |
p |
|
1 |
| |
1; |
|
|
|
||||||||||||||||||||||||||||||
|
|
p |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
метод Ньютона сходится с линейной скоростью, |
|
если p |
1 и, так как |
|||||||||||||||||||||||||||||||||||||
xn |
|
x |
|
|
p |
1 |
|
(xn |
|
x |
) |
|
O(| xn |
|
x |
| 2 ), |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
x |
|
|
|
p |
1 |
(xn |
|
|
x |
) |
|
O(| xn |
|
x |
|
| 2 ), |
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
p |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
xn |
1 |
xn |
|
|
|
|
|
|
O(| xn |
1 |
x | |
2 |
|
|
| xn |
|
|
x |
| |
2 |
) ; |
(5) |
||||||||||||||||
xn 2 |
|
|
2xn 1 |
|
xn |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
метод Ньютона сходится с квадратичной скоростью, если p |
|
1. |
|
|||||||||||||||||||||||||||||||||||||
50
