
VMLA-Matzokin-2012 / 2012-лекции ЧА
.pdf
Мацокин А.М. “Численный анализ”. Конспект лекций.
Лемма 1. Вторые производные ci s (xi ) от сплайна s(x) во |
внутренних |
||
узлах сетки |
h |
аппроксимируют вторые производные |
fi f (xi ) |
от функции f (x) |
C4[a, b] со вторым порядком точности по h : |
||
c |
f |
i |
r , |
| r | |
0.75 h2 |
M |
4 |
, |
i |
|
0, ..., n, |
|
M |
4 |
|
|| f (4) || |
C[a,b] |
. |
||||||||||||||||||
i |
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Теперь мы можем оценить r (x) |
f |
(x) |
s (x), |
x |
|
|
|
[xi , xi 1] . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Лемма 2. Вторая |
производная |
сплайна |
|
s (x) |
|
|
|
аппроксимирует |
вторую |
|||||||||||||||||||||||||||
производную |
f (x) |
|
|
от |
функции |
f (x) |
|
|
|
C4[a, b] |
|
в |
равномерной |
|||||||||||||||||||||||
норме со вторым порядком точности по h : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
| f |
(x) |
s (x) | |
0.875 |
h2 |
M4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
||||||||||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Неравенство (8) достаточно установить для любой точки x |
|
|
[xi , xi |
1] . |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Перепишем (5) в виде |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
f |
(x) |
|
|
|
|
|
r (x) |
f |
(x) |
s (x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
fi |
|
|
|
|
|
f |
i |
1 |
|
|
f |
|
(x) |
[f |
i |
|
xi |
1 |
|
x |
|
f |
i |
1 |
x |
|
xi |
] |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
h |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ci |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
s (x) |
ci 1 |
|
|
|
|
xi |
|
x |
|
|
|
|
x |
|
xi |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
[ri |
1 |
|
|
ri |
1 |
|
]. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
xi |
|
|
x |
|
xi |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из леммы 1 следует, что | r |
|
|
xi 1 |
x |
|
r |
|
1 |
x |
xi |
|
| |
0.75 h2 |
|
M |
4 |
. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
i |
|
|
h |
|
i |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя явный вид ошибки линейной интерполяции функции f (x)
| f (x) [f |
i |
xi 1 x |
f |
i |
1 |
x |
|
xi |
] | | |
f (4) ( (x)) |
(x x |
)(x |
|
|
|
|
|
|
|||||||||
|
h |
|
|
h |
|
|
2 |
|
i |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0.125 M4 h2 |
|
|
||
получим для любой точки x |
|
[xi , xi 1] |
|
|
|
||||||||
|
|
|
| f |
(x) |
|
s (x) | |
0.875 h2 M4, |
|
|
||||
что и требовалось доказать.
Из неравенств (4) и (8) получаем оценку погрешности. Теорема 1. Для погрешности аппроксимации f (x) C4[a, b]
справедливы следующие оценки:
xi 1) |
сплайном s(x)
|| f (k) (x) s(k) (x) || C[a,b] 0.875 h4 k M4, k 0,1, 2 .
21

Мацокин А.М. “Численный анализ”. Конспект лекций.
Численное дифференцирование
Для приближения значения производной f ( j) (x |
) |
|
функции |
f (x) |
обычно |
|||||||||||||||||||||||||||||||||||||||||
используется |
значение |
производной |
Pn( j) (x ) |
|
интерполяционного полинома |
|||||||||||||||||||||||||||||||||||||||||
Pn (x) (построенного по заданным значениям fk |
|
|
|
f (xk ) в узлах x0 , ..., xn ): |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( j) (x |
|
|
) |
|
|
Pn( j) (x |
) |
(kj) (x ) fk |
|
|
|
|
|
k (x ) |
fk , |
|
|
|
(9) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где коэффициенты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
k (x ) |
( j) |
(x ) ( |
|
d j |
|
|
(x |
x0 )...(x |
|
|
|
xk |
1)(x |
|
xk |
1)...(x |
xn ) |
) |x x |
||||||||||||||||||||||||||||
k |
d x j (xk |
x0 )...(xk |
|
|
|
xk 1)(xk |
|
|
xk 1)...(xk |
xn ) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
не зависят от функции f (x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Оценить точность приближения производной, т.е. разность |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
f ( j) (x ) |
P( j) |
(x ) |
|
|
[f (x) |
P (x)]( j) |
|
| |
|
|
|
|
[ |
f (n |
1) ( |
(x)) |
(x)]( j) | |
|
, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
x x |
|
|
|
|
(n 1)! |
|
|
|
x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
довольно сложно: во-первых, мы не характеризовали функцию |
|
(x) ; во- |
||||||||||||||||||||||||||||||||||||||||||||
вторых, потребуется существование производных функции |
f (x) |
до порядка |
||||||||||||||||||||||||||||||||||||||||||||
n |
1 j. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка погрешности численного дифференцирования |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Поэтому |
для |
оценки |
разности f ( j) (x ) |
|
|
|
n |
|
|
|
k (x ) fk |
мы заменим fk |
||||||||||||||||||||||||||||||||||
|
|
|
k |
|
0 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
разложением в ряд Тейлора в точке x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
fk |
f |
(0) |
(x ) |
|
f |
(1) |
(x |
) |
(xk |
|
x |
) ... |
f |
(n) |
(x |
) |
(xk |
|
x )n |
k,n (x |
), |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
(10) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x )n |
1 |
|
|
||
|
|
k,n (x |
) |
|
|
1 |
|
xk |
f |
(n 1) |
(t) (xk |
t) |
n |
dt |
f |
(n |
1) |
( |
k ) |
|
(xk |
. |
|
|
||||||||||||||||||||||
|
|
|
|
|
n! |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
(n |
1)! |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда для любой функции f (x) |
Cn 1[a, b] имеем тождество |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
f ( j) (x |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
) |
|
|
|
|
|
k (x ) |
fk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
(xk |
|
|
x |
)0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
f |
|
|
|
|
(x |
) |
|
|
|
[ |
|
k (x |
) |
|
|
|
|
|
|
|
|
|
] |
|
... |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0! |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
( j 1) |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
(xk |
|
|
x |
) j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
f |
|
|
|
|
|
(x |
|
) |
|
|
[ |
|
k (x |
) |
|
|
|
|
|
|
|
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( j |
|
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
22

Мацокин А.М. “Численный анализ”. Конспект лекций.
|
|
|
|
|
( j) |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
(xk |
x ) j |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
f |
|
|
|
(x |
) |
[1 |
|
|
k (x |
) |
|
|
|
|
|
|
|
|
] |
|
|
|
|
|
|
|
(11) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
j! |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f |
( j |
1) |
(x |
) |
[ |
|
|
n |
k (x |
) |
|
|
(xk |
|
x |
) j |
1 |
] ... |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
( j |
1)! |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(n) |
|
|
|
|
|
|
|
n |
|
|
|
|
|
(xk |
|
x |
)n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
f |
|
|
|
(x |
) |
[ |
|
|
|
k (x |
) |
|
|
|
|
|
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k (x |
) |
|
|
|
k,n (x |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если в это тождество подставить функцию |
f (x) |
равную полиному |
Fn,m (x) |
|||||||||||||||||||||||||||||||||||
степени n , m -ая производная которого в точке |
x |
|
|
|
x |
|
равна 1, |
|
а значения |
|||||||||||||||||||||||||||||
остальных производных равны 0, |
т.е. функцию f (x) |
|
|
|
Fn,m (x) |
|
Pn (x) |
такую, |
||||||||||||||||||||||||||||||
что |
k,n |
(x) |
0, f (x) |
|
P (x) 0 и, следовательно, |
[f (x) |
|
P (x)]( j) |
| |
x |
0, то |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
x |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
(xk |
x )m |
|
|
|
|
||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
(x |
) |
|
|
|
|
|
|
|
|
, |
|
m |
j, |
|
0 |
Fn,m( j) |
(x ) |
|
|
|
|
k (x ) |
Fn,m (xk ) |
|
k 0 |
|
|
|
|
|
|
m! |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
(xk x )m |
|
|
||||||||||||||||||||||
|
|
|
|
k |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
k (x |
) |
|
|
|
|
|
, |
m |
j. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
0 |
|
m! |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из этого тождества сразу получаем следующую лемму. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Лемма 3. |
Коэффициенты |
|
|
|
|
(x |
) |
( |
|
|
|
|
|
(x) |
|
|
|
|
|
)( j) | |
|
|
|
|
из |
(9) |
||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
xk ) (xk ) |
x |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
удовлетворяют соотношениям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
n |
|
|
k (x |
) |
|
(xk |
x |
)m |
|
|
|
|
0, если m |
|
j, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
k 0 |
|
|
|
|
m! |
|
|
|
|
|
|
1, если m |
|
j, |
|
|
|
|
|
(12) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
0, ..., n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из (11) и леммы 3 получаем оценку погрешности численного дифференцирования.
Теорема 2. Для |
погрешности приближения |
f ( j) (x ) |
линейной комбинацией |
||||
n |
|
|
|
|
|
|
|
|
k (x ) |
fk |
из (9) имеет место представление |
|
|||
k 0 |
|
|
|
|
|
|
|
|
f ( j) (x |
|
n |
|
n |
|
|
|
) |
k (x ) |
fk |
[ k (x |
) k,n (x )] , |
(13) |
|
|
|
|
k 0 |
k |
0 |
|
|
где |
k,n (x) − остаточные члены разложений в ряды Тейлора (10). |
||||||
23
Мацокин А.М. “Численный анализ”. Конспект лекций.
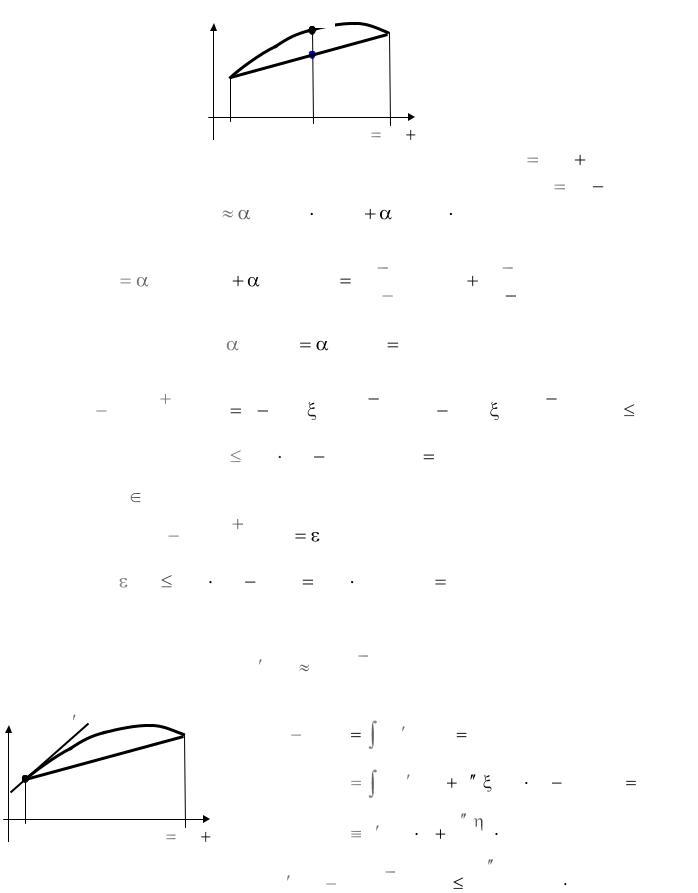
Аппроксимация значения функции в центре интервала полусуммой ее значений на краях интервала
f (x) f (x1/2 )
|
P1(x) |
|
|
|
x1/2 x1 |
x |
|
x0 |
x0 h |
|
|
Аппроксимация значения функции в центре |
интервала x1/2 (x0 |
x1) / 2 |
|
полусуммой ее значений на краях интервала [x0 , x1] малой длины h |
x1 x0 : |
||
f (x1/2 ) |
0 (x1/2 ) f (x0 ) |
1(x1/2 ) f (x1) . |
|
Так как интерполяционный полином по значениям f (x0 ) и f (x1) имеет вид
P (x) |
0 |
(x)f (x |
0 |
) |
1 |
(x)f (x ) |
x |
x1 |
f (x |
0 |
) |
x |
x0 |
f (x ) , |
|
|
|
|
|
||||||||||||
1 |
|
|
|
1 |
x0 |
x1 |
|
x1 |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
x0 |
|||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 (x1/2 ) |
1(x1/2 ) |
1/ 2 , |
|
|
|
|
|
|||
а из теоремы 2 имеем оценку
| f (x ) |
|
f (x0 ) |
f (x1) |
| |
| f (2) ( |
||||||||
|
|
|
|
||||||||||
1/2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
(x1 |
||
Итак, если f (x) |
C2[x0 , x1], то |
|
|
|
|||||||||
|
f (x1/2 ) |
|
f (x0 ) |
f (x1) |
|||||||||
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
| |
1/2 |
| |
M |
2 |
(x |
x |
0 |
)2 |
||||
|
|
|
|
|
|
1 |
|
|
|
||||
|
(x0 x1/2 )2 |
|
(2) |
|
|
|
(x1 |
x1/2 )2 |
||
0 ) |
|
f |
|
( |
1) |
|
|
|
| |
|
2! |
|
|
|
2! |
||||||
|
|
|
|
|
|
|
|
|
||
x0 )2 , M2 |
|| f || |
2 |
[x0 ,x1] |
. |
|
|
||||
|
|
|
C |
|
|
|
||||
1/2 , |
|
|
|
|
|
|
|
|
|
|
M2 h2 , M2 |
|| f || |
2 |
[x0 ,x1] |
. |
|
|||||
|
|
|
|
C |
|
|
||||
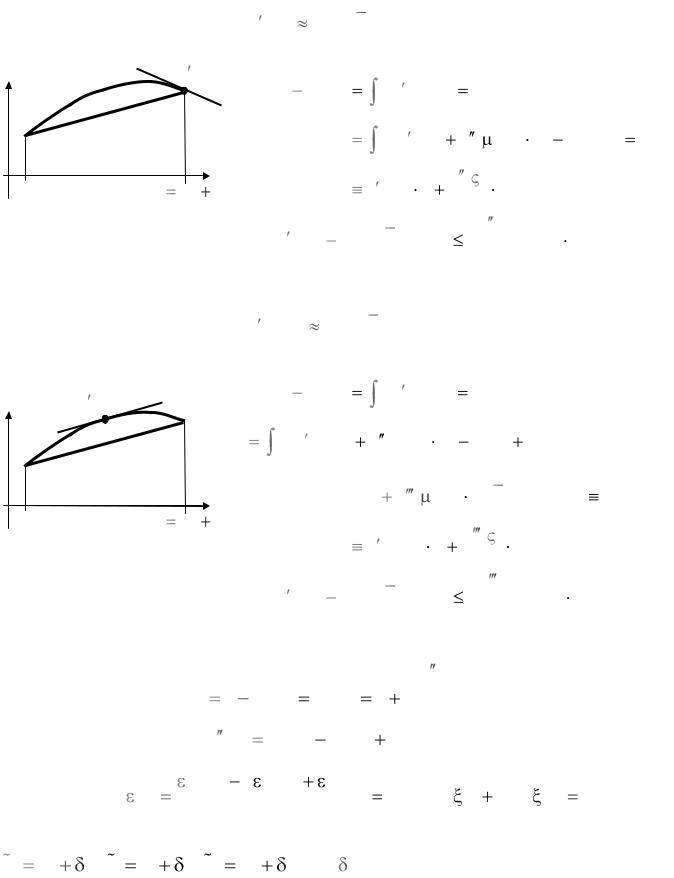
Аппроксимация производной разностью вперед |
|
|
|
|
|
|
|
||||||||||
|
|
|
f (x0 ) |
f (x1 ) |
f (x0 ) |
− разность вперед; |
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
h |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x0 ) |
|
f (x1) f (x0 ) |
|
x1 |
f (y) dy |
|
|
||||||||||
|
|
|
|
x0 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P1(x) |
|
|
|
|
x1 [f (x0 ) |
|
f ( |
(y)) (y |
x0 )] dy |
||||||
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
f ( ) |
h2 , |
|
|
x0 |
|
x1 x0 h |
|
|
|
f (x0 ) h |
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
f (x |
) f (x |
0 |
) |
|
|
|
|| f |
|| C[x ,x ] |
|
|||
|
|
|
то | f (x0 ) |
|
1 |
|
|
|
|
|
| |
|
|
0 1 |
h . |
||
|
|
|
|
h |
|
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
24
|
Мацокин А.М. “Численный анализ”. Конспект лекций. |
||||||||||||||||
Аппроксимация производной разностью назад |
|
|
|
|
|
|
|
|
|||||||||
|
|
f (x1 ) |
|
f (x1 ) |
f (x0 ) |
− разность назад; |
|||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
h |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
f (x1) |
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 f (y) dy |
|
||||||||||
|
f (x ) |
f (x |
0 |
) |
|
|
|||||||||||
|
|
1 |
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
P1(x) |
|
|
|
|
|
|
x1 [f (x ) |
|
f ( |
(y)) (y |
||||||
|
|
|
|
|
|
|
|
x0 |
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( ) |
h2 , |
|
x0 |
x1 x0 h |
|
|
|
|
|
f (x1) h |
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
f (x |
) f (x |
0 |
) |
|
|
|
|| f |
|| C[x ,x ] |
|||
|
|
то | f (x0 ) |
|
|
1 |
|
|
|
|
|
| |
|
|
0 1 |
|||
|
|
|
|
|
h |
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x1)] dy
h .
Аппроксимация производной центральной разностью
|
|
|
|
|
f (x1/2 ) |
f (x1) |
|
f (x0 ) |
|
− центральная разность; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
f (x ) f (x |
|
) |
x1 f (y) dy |
|
|
|
|
|
|
|
|
|
||||||||||
f (x1/2 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
0 |
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x1 [f (x |
|
|
|
) |
f |
(x |
|
|
) |
(y |
|
|
x |
|
) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
P (x) |
|
1/2 |
|
|
1/2 |
|
|
|
|
|
1/2 |
|
|
|
|
|
|||||||||
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(y |
|
x |
|
)2 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
f |
( |
|
(y)) |
|
|
|
|
1/2 |
|
] dy |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||
x0 |
x1/2 x1 |
x0 h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( |
) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h3, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
f (x |
|
) |
|
h |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1/2 |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
f (x ) |
f (x |
0 |
) |
|
|
|
|| f |
|| C[x |
|
,x ] |
h2 . |
||||||||
|
|
|
|
|
то | f (x0 ) |
|
|
|
|
1 |
|
|
|
|
|
|
| |
|
|
|
|
|
0 1 |
||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Некорректность численного дифференцирования
Выпишем аппроксимацию второй производной f (c) по трем значениям
функции f (x) в узлах x0 c |
h, x1 |
|
|
c, x2 |
|
|
c h : |
|
||||||||||||||
|
P (c) |
1 |
|
f |
|
2 |
|
f |
1 |
|
|
f |
|
. |
||||||||
|
|
|
2 |
|
0 |
|
|
2 |
|
|
|
|
2 |
|
2 |
|||||||
|
n |
|
h |
|
|
|
h |
|
1 |
|
|
h |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Докажите, что (c) |
0,1(c) 2 1,1(c) |
|
2,1(c) |
|
|
h2 |
|
[f (4) ( 0 ) f (4) ( 2 )] O(h2 ) . |
||||||||||||||
|
h2 |
|
|
|
|
|
|
|
|
|
|
24 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Предположим, что вместо точных значений f0 , f1, f2 заданы их приближения f0 f0 0 , f1 f1 1, f2 f2 2 , где i − ошибки округления. Тогда
25

Мацокин А.М. “Численный анализ”. Конспект лекций.
|
P (c) P (c) |
|
|
0 |
2 1 |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
n |
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (c) |
P |
|
(c) |
f |
(c) |
P |
(c) |
|
[P |
(c) |
P |
|
(c)] |
|
(c) |
|
|
0 |
|
2 1 |
2 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
n |
|
|
|
|
n |
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
h2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для большей |
наглядности будем |
|
предполагать, что |
f (4) ( ) |
|
M4 |
12 |
|||||||||||||||||||||
( f (x) |
− |
полином |
четвертой |
|
степени), |
0 |
|
|
2 |
|
|
|
, |
|
1 |
|
10 12 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(вычисления с 12-ю десятичными знаками), тогда |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
(c) |
f |
(c) |
P (c) |
|
(c) |
0 |
|
2 1 |
|
2 |
|
h |
2 |
|
4 |
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из последней формулы следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1. |
(c) |
|
|
при h |
0 (если h |
10 6 , то |
|
(c) |
|
4 вместо |
|
(c) 10 12 ); |
||||||||||||||||
2. |
для |
получения |
(c) |
O(h2 ) |
нет |
смысла |
брать |
|
h |
|
1/ 4 |
|
и при |
|||||||||||||||
|
h |
1/ 4 |
|
10 3 мы получим наилучшую точность |
(c) |
|
O(h2 ) |
5 10 6 . |
||||||||||||||||||||
26

Мацокин А.М. “Численный анализ”. Конспект лекций.
Лекция 4. Численное интегрирование
Интегрирование функций является одной из основных математических операций. В этом разделе мы рассмотрим классический подход к построению интерполяционных квадратурных формул для приближенного вычисления определенного интеграла
I |
ab f (x) |
p(x) dx, |
f (x) C[a, b] , |
|
(1) |
||
где p(x) − положительная функция такая, что |
b xk p(x) dx |
k |
0 . |
||||
|
|
|
|
|
a |
|
|
Определение 1. Формула |
|
|
|
|
|
|
|
|
In |
n |
Ak |
f (xk ) |
|
(2) |
|
|
k 0 |
|
|||||
|
|
|
|
|
|
|
|
называется квадратурной формулой для приближенного вычисления |
|||||||
интеграла (1) от функции f (x) на (n |
1) -ом узле a x0 |
x1 ... |
xn b |
||||
с весами A0 , A1, ..., An . |
|
|
|
|
|
|
|
Так как по значениям функции f (x) |
в узлах квадратурной формулы мы можем |
|||||||||||||||
построить интерполирующий ее полином в форме Лагранжа |
|
|||||||||||||||
|
|
Pn |
(x) |
|
n |
|
|
|
|
|
|
(x) |
|
|
f (xk ) , |
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
k 0 (x |
|
x |
k |
) (x |
k |
) |
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
(x) (x x0 ) (x |
x1) ... (x |
|
xn ) , то естественным было бы |
||||||||||||
определить веса квадратурной формулы (2) в виде |
|
|
|
|
||||||||||||
|
Ak |
b |
|
|
(x) |
|
|
|
|
p(x) dx, |
k 0,1,..., n , |
(4) |
||||
|
a |
|
|
|
|
|
|
|
||||||||
|
(x x |
k |
) |
(x |
k |
) |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а саму формулу назвать интерполяционной квадратурной формулой.
Определение 2.
Квадратурная формула (2) называется интерполяционной квадратурной формулой, если ее веса вычисляются по формуле (4).
Практически очевидно, что интерполяционная квадратурная формула (2) будет точна (т.е. I In ), если функция f (x) является полиномом степени не более, чем n . И обратно, если квадратурная формула (2) точна на любом полиноме
степени n , |
то она должна быть интерполяционной, т.е. для ее весов должна |
|||||||
быть |
справедлива |
формула |
(4), |
что |
легко |
проверить, |
взяв |
|
f (x) |
|
(x) |
при любом k 0, 1, ..., n . |
|
|
|
||
|
|
|
|
|
||||
(x |
xk ) (xk ) |
|
|
|
||||
|
|
|
|
|
|
|
||
Определение 3.
Алгебраической степенью точности квадратурной формулы (2) называется целое число m такое, что квадратурная формула точна на всех полиномах степени m и меньше.
27

Мацокин А.М. “Численный анализ”. Конспект лекций.
Теорема 1. |
Квадратурная формула (2) на (n |
1) узле будет интерполяционной |
|
квадратурной формулой тогда и только тогда, если она имеет |
|
|
алгебраическую степень точности n . |
|
Теорема 2. |
Если функция f (x) Cn 1[a, b], |
то для разности интеграла (1) и |
|
его приближения интерполяционной квадратурной формуле (2) |
|
|
справедлива оценка |
|
|| f (n 1) |
(x) || C[a,b] |
b |
|
|
||
| I In | |
|
|
a |
| (x) | p(x) dx . |
(5) |
|
(n 1)! |
||||||
|
|
|
||||
Докажите эту теорему, используя оценку для погрешности интерполирования функции и теорему 1.
Квадратуры Гаусса наивысшей алгебраической степени точности
Итак, на любой системе узлов a x0 x1 ... xn b интерполяционная
квадратурная формула (2) точна на линейном пространстве размерности n 1 всех полиномов степени не более, чем n .
Естественным образом возникает вопрос: а нельзя ли за счет выбора этих узлов ( n 1 параметр) увеличить алгебраическую точность квадратурной формулы? Квадратурная формула (2) определяется 2(n 1) параметрами и можно
надеяться, что их можно выбрать так, формула будет точна для полиномов
степени 2n 1, но не более. |
|
|
Теорема 3. Квадратурная формула (2) на n |
1 |
узле не может иметь |
алгебраическую степень точности m |
2n |
1. |
Доказательство (от противного).
Предположим, что квадратурная формула алгебраической степени
точности m |
2n 1 существует. |
|
|
|
|
|
|
|
|
|
|||||
Тогда |
по |
теореме 1 |
она |
является |
интерполяционной |
и |
точна |
на |
|||||||
f (x) |
2 (x) − полиноме степени 2n |
2 |
m , т.е. I |
In . Но |
|
|
|
||||||||
In |
0 , так как |
2 (xk ) |
0 (узлы квадратуры − корни полинома |
(x) ), |
|
||||||||||
I |
0 , так как функция f (x) |
2 (x) |
0 почти всюду на [a, b] . |
|
|
|
|||||||||
Следовательно, полученное |
противоречие I |
In предположению |
I |
In |
|||||||||||
доказывает теорему. |
|
|
|
|
|
|
|
|
|
|
|
||||
Теорема 4. Если |
квадратурная |
формула |
(2) |
на |
n 1 |
узле |
имеет |
||||||||
|
|
алгебраическую |
степень |
|
точности |
m |
2n |
1, |
то |
|
она |
||||
|
|
интерполяционная, |
а |
полином |
(x) |
(x |
x0 )...(x |
|
xn ) |
||||||
ортогонален с весом p(x) всем полиномам меньшей степени, т.е. определяется условиями:
b |
(x)xi |
p(x) dx 0, i 0, 1, ..., n . |
|
a |
|||
|
|
Доказательство.
Пусть квадратурная формула алгебраической степени точности m 2n 1 существует. Тогда по теореме 1 она является интерполяционной.
28

Мацокин А.М. “Численный анализ”. Конспект лекций.
Так |
как |
степень полинома |
f (x) |
(x) |
xi , 0 i n , |
не превышает |
|||
m |
2n 1, то квадратурная формула (2) точна на нем и |
|
|||||||
|
|
b |
(x)xi p(x) dx |
n |
Ak |
(xk )xik |
0, |
||
|
|
a |
k 0 |
||||||
|
|
|
|
|
|
|
|
||
что и требовалось доказать. |
|
|
|
|
|
|
|||
Теорема 5. Если полином (x) (x |
x0 )...(x |
|
xn ) |
ортогонален с весом p(x) |
|||||
|
всем полиномам меньшей степени, то интерполяционная |
||||||||
|
квадратурная формула (2) имеет алгебраическую степень точности |
||||||||
|
m |
2n 1. |
|
|
|
|
|
|
|
Доказательство.
Так как квадратурная формула (2) интерполяционная, то по теореме 1 она точна на полиномах до степени n .
Произвольный полином |
Lt (x) степени t m 2n 1 мы |
можем |
представить в виде Lt (x) |
(x) Qn (x) Rr n (x) , разделив Lt (x) на |
(x) . |
Тогда |
|
|
I |
|
b Lt (x) |
p(x) dx |
b (x) Qn (x) p(x) dx |
b R r |
n (x) p(x) dx |
|
a |
|
a |
a |
|
|
|
0 |
n |
Ak Rr n (xk ), |
|
|
|
|
k 0 |
|
|
|||
|
|
|
|
|
|
|
так |
|
как по |
условию |
теоремы полином |
(x) |
ортогонален полиномам |
меньшей степени, а интерполяционная квадратурная формула (2) точна на полиномах степени r n .
С другой стороны,
In |
n |
Ak |
[ (xk ) Qn (xk ) Rr n (xk )] |
n |
|
Ak [0 Rr n (xk )] I , |
|
k 0 |
k |
0 |
|||||
|
|
|
|
что и требовалось доказать.
Таким образом, интерполяционная квадратурная формула (2) существует тогда и только тогда, когда (теоремы 4 и 5) существует полином (x) ,
ортогональный с весом p(x) полиномам меньшей степени, с попарно различными корнями из интервала [a, b] .
Теорема 6. Полином |
(x) |
xn 1 |
an xn ... |
a0 , ортогональный с весом |
||
p(x) всем полиномам меньшей степени: |
|
|||||
|
b |
(x)xi p(x) dx 0, i |
0, 1, ..., n , |
|
||
|
a |
|
||||
|
|
|
|
|
|
|
существует, единственен и имеет n |
1 простых корней на |
[a, b] , |
||||
т.е. |
(x) |
(x |
x0 )...(x |
xn ) , |
xk [a, b], xi x j − |
узлы |
квадратуры (Гаусса) наивысшей алгебраической степени точности.
Доказательство.
Очевидно, что для определения коэффициентов a0 , ..., an полинома (x) мы имеем систему линейных алгебраических уравнений
29

Мацокин А.М. “Численный анализ”. Конспект лекций.
b |
(an xn |
... a0 ) xi p(x) dx |
b xn 1 |
xi |
p(x) dx, i 0, 1, ..., n . (6) |
a |
|
|
a |
|
|
Для существования и единственности ее решения необходимо и достаточно, чтобы однородная система
b |
(an xn |
... a0 ) xi p(x) dx 0, i 0, 1, ..., n , |
a |
|
|
имела только нулевое решение. Предположим, что однородная система (6) имеет решение a0 , ..., an . Тогда, умножив i -е уравнение на ai и сложив результаты, получим
b |
(an xn |
... a0 )2 p(x) dx 0, |
a |
|
|
откуда следует, что все a0 , ..., an должны быть равны нулю. Осталось исследовать корни полинома (x) .
Предположим, что все вещественные корни {xi [a, b]}im 0 полинома
(x) , имеют четную кратность 2ki ,
т.е. (x) [(x x |
0 |
)k0 |
...(x |
x |
m |
)km ]2 |
|
... k |
|
) |
(x) , где полином |
|
|
|
|
n 1 2(k |
0 |
m |
|
||||
|
|
|
|
|
|
|
|
|
|
n 1 2(k0 ... km ) (x) знакоопределен на [a, b] .
Но, так как |
|
|
b |
|
(x) |
|
p(x) dx |
|
|
0 , то полином |
|
|
|
|
|
|
|
|
|
) (x) должен |
|||||||||||||||||||
|
a |
|
|
|
|
n |
1 |
|
2(k |
0 |
... |
k |
m |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
менять знак на [a, b] , что противоречит выводу из предположения о |
|||||||||||||||||||||||||||||||||||||||
четности всех корней из [a, b] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Следовательно, полином |
|
(x) имеет на [a, b] корни нечетной кратности. |
|||||||||||||||||||||||||||||||||||||
Пусть {xi |
[a, b]}im |
0 − корни нечетной кратности 2ki |
|
1 полинома |
|
(x) . |
|||||||||||||||||||||||||||||||||
Если |
m |
n |
|
|
1 |
( ki |
|
1), |
|
то |
все корни попарно |
|
различны |
|
и |
|
|
теорема |
|||||||||||||||||||||
доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если m |
n |
|
1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(x) |
[(x |
x |
0 |
)k0 ...(x |
x |
m |
)km |
]2[(x |
x |
0 |
)...(x |
x |
m |
)] |
n |
1 2(k |
0 |
... k |
m |
) |
m |
(x) , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где полином |
|
|
n |
1 2(k |
0 |
... k |
m |
) |
m (x) знакоопределен на [a, b] . |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Но, так как степень полинома (x |
|
x0 )...(x |
|
xm ) |
|
меньше n |
|
1, |
то |
|
(x) |
||||||||||||||||||||||||||||
ему ортогонален, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
b [(x |
x |
0 |
)k0 1...(x |
x |
m |
)km 1]2 |
n |
1 2(k |
0 |
... k |
m |
) |
m |
(x) |
p(x) dx |
0 , |
|||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда следует, |
что |
|
n |
1 |
|
2(k |
0 |
... k |
m |
) m (x) должен менять знак на [a, b] , |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
что противоречит выводу из предположения о знакоопределенности . |
|||||||||||||||||||||||||||||||||||||||
Следовательно, |
m |
n и теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Теорема 7. Если |
|
|
функция |
|
f (x) |
C2n |
2[a, b] , |
то |
|
точность |
|
вычисления |
|||||||||||||||||||||||||||
|
интеграла (1) по квадратурной формуле Гаусса (2) |
на |
n |
|
1 узле |
||||||||||||||||||||||||||||||||||
|
оценивается следующим неравенством: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
30
