Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

VMLA-Matzokin-2012 / 2012-лекции ЧА

.pdf

Скачиваний:

106

Добавлен:

06.06.2015

Размер:

2.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Мацокин А.М. “Численный анализ”. Конспект лекций.

\|\| f 2(n 1)		(x) \|\| C[a,b]	b	\| (x) \| 2
\| I In \|			a		p(x) dx .	(7)
	(2n 2)!

Доказательство оставляется в качестве упражнения.

Сходимость квадратур Гаусса

Замечательным свойством квадратур Гаусса является их сходимость для любой

функции

f (x)

C[a, b]

(заметим, что интерполяционный полином к

произвольной непрерывной функции не сходится).

Теорема 8. Если функция

f (x)

C[a, b], то интерполяционная квадратурная

формула (2) на

1 узле

x0 , ..., xn

с положительными весами

A0 , ..., An сходится к интегралу (1) при n

Доказательство.

Поскольку

f (x)

C[a, b],

то

по

теореме

Вейерштрасса

существует полином QN( ) (x) такой, что

| f (x)

QN( ) (x) |

0.5

[a, b].

Тогда для

N( )

интерполяционная квадратурная

формула

(2) на

попарно различных узлах x0 , ..., xn точна на полиноме QN( ) (x) и

f (x) p(x) dx

fk |

[f (x)

QN( ) (x)]

p(x) dx

QN( )

(x) p(x) dx

QN( ) (xk )

k 0

Ak (QN( )

(xk ) fk ) |

k 0

0.5

[

p(x) dx

Ak ]

p(x) dx

при

что и требовалось доказать.

Лемма. Веса квадратур Гаусса положительны.

Квадратура Гаусса (2) точна на полиномах до степени 2n

1 и значит она

точна на полиноме f (x)

g2 (x)

[(x

x0 )...(x

xi 1)(x

1)...(x

xn )]2

степени 2n :

f (x)

p(x) dx

f (xk )

Ai g2 (xi ) 0

0 .

Устойчивость квадратурных формул

Зачастую, по тем или иным причинам, значения интегрируемой функции в

узлах заданы с погрешностью: f (xk )		f (xk )	k , \|	k \|	.
Тогда
\| I In \| \| I In \| \| In In \| \| I In	\|	n	\| Ak \|	\| I	In \|	b	p(x) dx
\| I In \| \| I In \| \| In In \| \| I In	\|	k 0	\| Ak \|	\| I	In \|	a	p(x) dx
		k 0				a

Мацокин А.М. “Численный анализ”. Конспект лекций.

если квадратура точна на константе и ее веса положительны.

Отсюда следует, что малые изменения интегрируемой функции мало изменяют приближенное значение интеграла независимо от числа квадратурных узлов.

Примеры квадратурных формул

В этом разделе для приближенного вычисления определенного интеграла

I	ab f (x) dx,			f (x)		C[a, b]				(1)
1. мы построим примеры интерполяционных квадратурных формул
	In	n			Ak	f (xk )				(2)
		k	0

на (n 1) -ом узле a	x0 x1			... xn				b с весами
Ak	b				(x)				dx, k 0,1,..., n ,	(3)

	a (x		x	k	)	(x	k	)

2.найдем их алгебраическую степень точности m : для этого необходимо и достаточно найти максимальное целое m такое, что

I	b	xi dx In	n		Ak		(xk )i , i 0, 1, ..., m;
	a		k 0
								(4)
	b			n
I		xm 1 dx In				Ak		(xk )m 1;
	a			k 0

3. конкретизируем оценку погрешности интерполяционной квадратуры на

(n 1) -ом узле алгебраической степени точности m							n :
\| I In \|	\|\| f (m 1) (x) \|\| C[a,b]		b	\|	(x)	dn,m (x) \|dx ,		(5)
		(m 1)!	a

где
dn,m (x)	1,		m		n;
	(x y1) ... (x yt ),		t		m	n,	y j [a, b].

Мацокин А.М. “Численный анализ”. Конспект лекций.

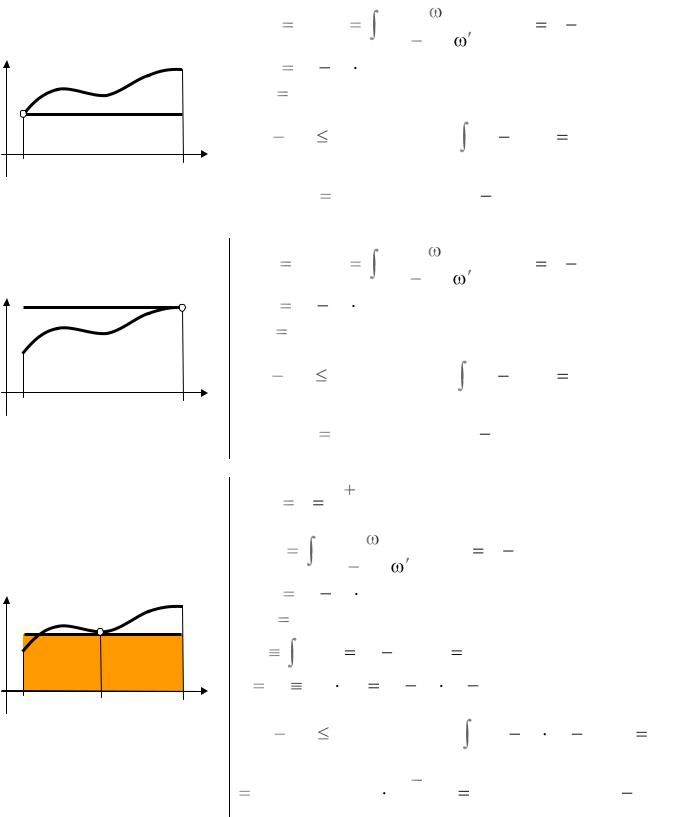
Формулы прямоугольников (на одном узле)

1. x0

a , A0

(x)

dx b a ,

f (x)

a (x

)

(b a) f (a) ,

P0 (x)

2. m

0 ,

|| f (1)

(x) || C[a,b]

3. | I

I0 |

| x

a |dx

|| f (1) (x) || C[a,b]

a)2 .

f (x)

P0 (x)

		x
a
	b

f (x)

P0 (x)

a	c	x
		b

1. x0

b , A0

(x)

dx b a ,

)

f (b) ,

0 ,

3. | I

I0 |

|| f (1) (x) || C[a,b]

| x

b |dx

|| f (1) (x) || C[a,b]

a)2 .

(x)

dx b

a ,

)

f (c) ,

2. m

1, так как

b x dx

a)2 / 2

A0 x0

(b a) (b a) / 2,

3. | I

I0 |

|| f (2) (x) || C[a,b]

| (x

c) (x c) |dx

|| f (2) (x) || C[a,b]

a)3

|| f

(2) (x) || C[a,b]

(b a)3 .

Мацокин А.М. “Численный анализ”. Конспект лекций.

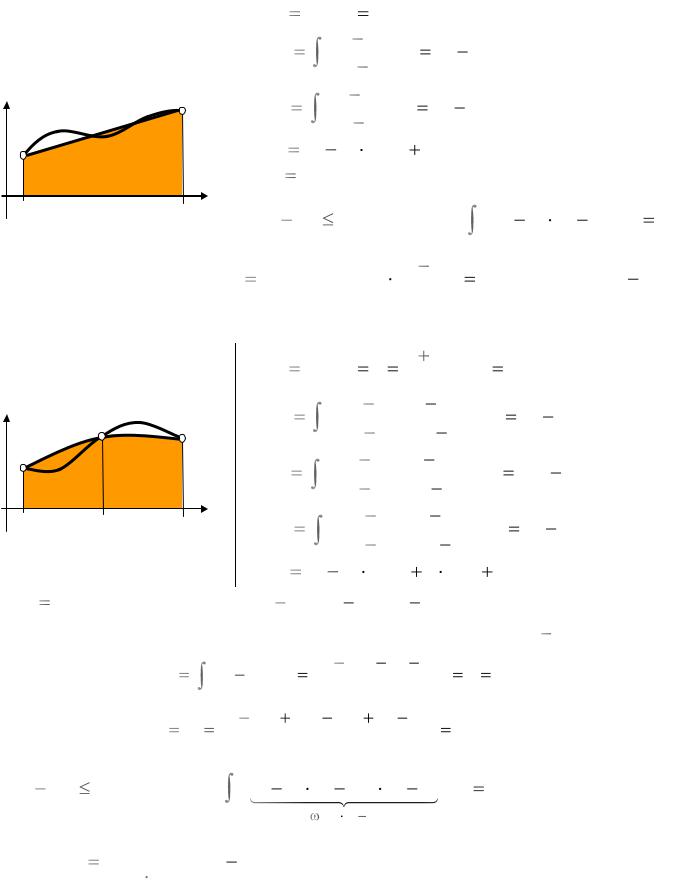
Формула трапеций (на двух узлах)

b ,

x x1

dx (b a) / 2,

f (x)

P (x)

a) / 2 ,

a) [f (a)

f (b)] / 2,

3. | I

I1 |

|| f (2) (x) || C[a,b]

| (x a) (x b) |dx

|| f (2) (x) || C[a,b]

a)3

|| f (2) (x) || C[a,b]

(b a)3 .

Формула Симпсона (на трех узлах)

1.	x		a, x	c	a b	, x		b ,
		0					2
			1		2

f (x)

x1)(x x2 )

a) / 6 ,

P (x)

x )(x

x )

x0 )(x

x2 )

4(b

a) / 6 ,

a (x

)(x

)

x0 )(x

x1)

a) / 6 ,

)(x

x )

a) [f (a)

f (c) f (b)] / 6 ,

2. m

3, так как на полиномах (x

c)0 , (x c)1, (x

c)2 формула точна в силу

ее интерполяционности и, кроме того, она точна на полиноме (x

c)3 :

c)3 dx

c)4

c)3

4(c

c)3

|| f (4)

(x) || C[a,b] b

c)2

3. | I

I2 |

| (x

a) (x

b) |dx

(x) (x c)

|| f (4) || C[a,b]

a)5 .

4! 120

Мацокин А.М. “Численный анализ”. Конспект лекций.

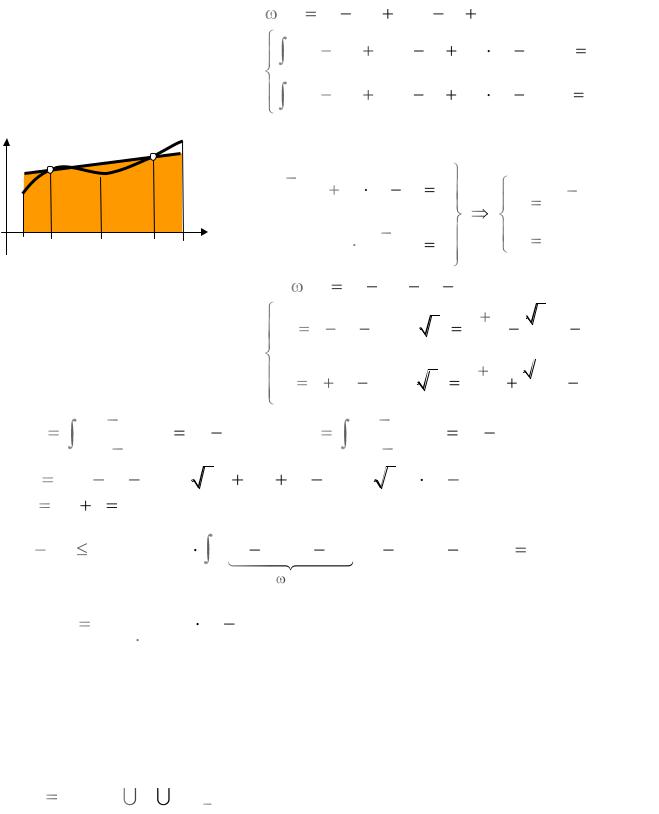
Квадратура Гаусса на двух узлах

1. Узлы x0 , x1 – корни полинома

(x) (x

c)2

a (x c)

такого, что

b[(x

c)2

a (x

]

c)0 dx

[(x

c)2

a1(x

a0 ]

c)1dx

f (x)

после вычисления интегралов эта система имеет

P1(x)

вид:

a)3

(b a)

a)2

a)3

x1 b

т.е. (x)

c)2

a)2 / 12 и его корни

a) / (2

a),

a) / (2

a);

x x1

dx (b a) / 2,

x x0

dx (b a) / 2 ,

a x

[f (c

(b a) / (2

3))

f (c (b

a) / (2

3))] (b

a) / 2 ,

2. m

3. | I

I1 |

|| f (4) || C[a,b]

[(x x0 )(x

x1)](x

x0 )(x

x1) dx

(x)

|| f (4) || C[a,b]

a)5 .

4! 180

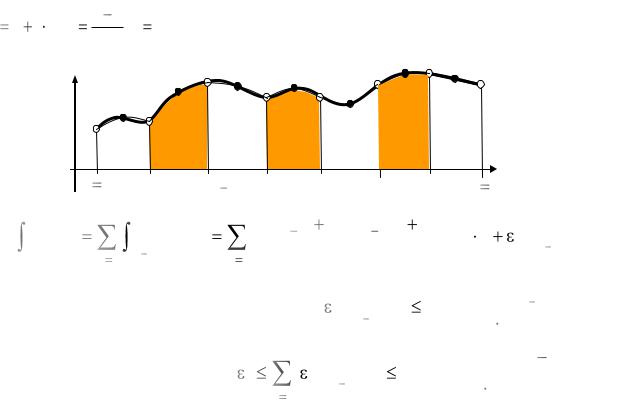
Составные квадратурные формулы

Использование простейших квадратурных формул для интегрирования функции на интервале, длина которого не является малой величиной, редко приводит к хорошим результатам. Поэтому отрезок интегрирования [a, b]

обычно	разбивают	на непересекающиеся	подъинтервалы малой	длины:
[a, b]	[x0 , x1] ...	[xN 1, xN ] , исходный	интеграл представляют	в виде

суммы интегралов по отрезкам разбиения и каждый интеграл этой суммы заменяют по той или иной простейшей квадратурной формуле:

Мацокин А.М. “Численный анализ”. Конспект лекций.

f (x)dx

In,[x

] .

k 1

]

k 1

n,[x

k 1

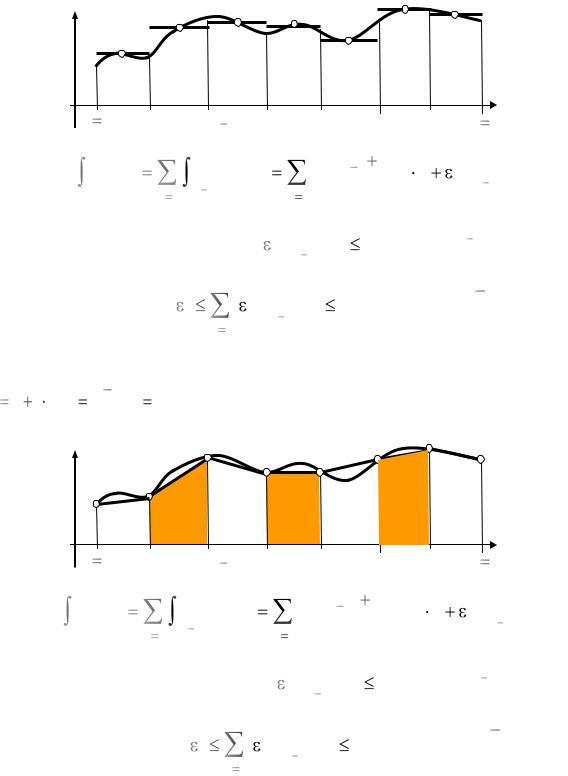
Составные формулы прямоугольников на равномерной сетке

a i h, h

b a

, i

0,..., N .

f (x)

a x0

xk 1

f (x)dx

[f (xk

1) h n,[x

] ],

xk 1

k 1

| n,[x

] |

|| f (1) (x) || C[xk 1,xk ]

|| f

(1)

(x) || C[a,b] (b

n,[x

,x ]

k 1

f (x)

a x0

xk 1

f (x)dx

[f (xk ) h n,[x

] ],

k 1

n,[x

] |

|| f (1)

(x) || C[xk 1,xk ]

(1)

|| f (x) || C[a,b] (b

| |

n,[x

,x ]

k 1

Мацокин А.М. “Численный анализ”. Конспект лекций.

f (x)

a x0

xk 1

f (x)dx

[f (

) h

n,[x

]

k 1

| n,[x

] |

|| f (2) (x) || C[xk 1,xk ]

k 1 k

|| f

(2)

(x) || C[a,b] (b

| |

] |

n,[x

k 1

Составная формула трапеций на равномерной сетке

xi a i h, h

b a

, i

0,..., m .

f (x)

a x0

xk 1

f (x

)

f (x

)

f (x)dx

[

) h

n,[x

]

k 1

n,[x

] |

|| f (2) (x) || C[xk 1

,xk ]

|| f

(2)

(x) || C[a,b] (b

h2.

| n,[x

] |

1 k

Мацокин А.М. “Численный анализ”. Конспект лекций.

Составная формула Симпсона на равномерной сетке xi a i h, h bma , i 0,..., m .

f (x)

a x0

xk 1

N xk

N f (x

) 4f (x

) f (x

)

1/2

f (x)dx

[

)

n,[x

]

xk 1

k 1

n,[x

,x ] |

|| f (4) (x) || C[xk 1,xk ]

(4!) 120

|| f

(4)

(x) || C[a,b] (b

h4.

| n,[x

] |

k 1

(4!) 120

k 1

Мацокин А.М. “Численный анализ”. Конспект лекций.

Лекция 5.

Итерационные методы решения нелинейных уравнений

При построении квадратур Гаусса необходимо находить корни полинома (x) степени n 1 (ортогонального полиномам меньшей степени), т.е. решить нелинейное уравнение (x) 0 .

Решать нелинейные уравнения необходимо, например, и при реализации простейшей неявной разностной схемы, аппроксимирующей задачу Коши для дифференциального уравнения первого порядка:

	du(t)	f (t, u(t)), t (0, T],

	dt
	dt
	u(0) u0 ,
на сетке {a t0 t1 ... tM	b} с “малыми” шагами k tk tk 1 .
u(t)	y(t)

tk 1

Схема строится очень просто:

1) интегрируем уравнение по интервалу [tk 1, tk ] :

f (tk

1, u(tk 1))

f (tk , u(tk ))

u(tk )

u(tk

f (t, u(t)) dt

k ,

1, ..., M,

u(0) u0 ,

2) удаляем в этой системе ошибки аппроксимации

O( 3k ) и получаем

для yk

u(tk ) уравнения:

yk 1

f (tk 1, yk 1) f (tk , yk )

k ,

k 1, ..., M.

Очевидно, что для вычисления yk

при

известном

нужно

решить

уравнение

f (tk , y)

[yk

f (tk 1, yk 1)

k ]

0 ,

т.е. найти корень уравнения F(y)

f (tk , y)

k [yk 1

f (tk 1, yk 1)

k ] 0 .

Сходимость y(t) к u(t) при

0 мы оставим на 3-й курс.

Мацокин А.М. “Численный анализ”. Конспект лекций.

Итак, пусть функция f (x) C[a, b] и требуется решить уравнение

f (x) 0 ,

(1)

решение x [a, b] которого будем называть корнем (нулем) функции f (x) .

Отметим, что каких-либо общих правил анализа расположение корней произвольной непрерывной функции f (x) на отрезке [a, b] не существует.

Определение 1.

Корень x	[a, b] функции f (x) будем называть изолированным корнем
кратности p	0 , если
	f (x)	(x	x )p g(x) ,		(2)
где функция g(x) непрерывна на			отрезке	[a, b] и знакоопределена в
некоторой окрестности I (x )		[x	, x	] [a, b],	0.

Очевидно, что, найдя один изолированный корень функции f (x) и определив его кратность, следующий корень мы можем искать как корень функции g(x) .

Постройте метод деления пополам для приближения корня в случае f (a) f (b) 0.

Построить явные формулы, определяющие корни непрерывной функции, удается крайне редко, поэтому основными методами решения задачи (1) являются итерационные процессы, позволяющие получить ее решение с любой точностью. Мы ограничимся изучением двух методов: метода последовательных приближений и метода Ньютона, основой которых является принцип сжимающих отображений.

Принцип сжимающих отображений

Пусть M − метрическое пространство с расстоянием (x, y) x, y M :

(x, x)	0,
(x, y)	(y, x)	0	x	y M,
(x, y)	(x, z)	(z, y)		x, y, z M.

Определение 2. Отображение
		: M		M ,			(3)
называется сжимающим, если			0	q 1 такое, что
	(	(x), (y) )	q	(x, y)	x, y	M .	(4)
Определение 3.
Элемент	x M	называется		неподвижной		точкой	отображения
: M	M , если
		x	(x ) .				(5)

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в папке VMLA-Matzokin-2012

#
06.06.20154.66 Mб3282012-лекции BMLA.pdf
#
06.06.20152.51 Mб1062012-лекции ЧА.pdf
#
06.06.201568.61 Кб582012-Программа ВМЛА+ЧА.doc
#
06.06.2015157.72 Кб552012-Программа ВМЛА+ЧА.pdf