Глава III

Синтез цифровых систем управления

методом пространства состояний

III.1. Представление моделей объектов управления

в пространстве состояний

Удобным и единообразным по форме является представление математической модели объекта в виде системы дифференциальных уравнений первого порядка, разрешенных относительно первых производных, т.е. уравнений в форме Коши. Для этого необходимо ввести дополнительные переменные, называемые переменными или координатами состояния объекта. Модель объекта в этом случае будет определяться через функциональную связь трех видов переменных: входных u_i, выходных y_i и внутреннего состояния х_i.

(3.1)

где F_C и F_B – функции состояния и выхода объекта;

U, X, Y – векторные величины, компонентами которых являются переменные u_i, x_i, y_i.

Чтобы лучше разобраться в особенностях описания объекта через переменные состояния, рассмотрим уравнение первого порядка

(3.2)

Введем обозначение y = x и представим уравнение (3.2) в форме (3.1.)

(3.3)

.

Структурная схема системы (3.3) представлена на рис. 3.1, а.

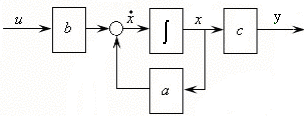
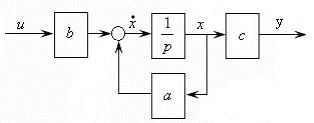
а)непосредственная форма описания б) символьная форма описания

Рис. 3.1.Структурная схема описания объекта регулирования первого

порядка с использованием переменной состояния х

Чаще всего операцию интегрирования всех структурных схем обозначают через оператор 1/р. (см. рис. 3.1, б) Объект, описываемый дифференциальным уравнением n-го порядка, через переменные состояния будет представляться

n- дифференциальными уравнениями первого порядка (в форме Коши)

(3.4)

где х₁, … х_n – переменные или координаты состояния.

Кроме того, согласно (3.1), требуется уравнение выхода, которое в общем случае будет иметь следующий вид

(3.5)

Уравнения (3.4) и (3.5) справедливы для объекта с одним входом и одним выходом, т.е. когда y, u – скалярные величины. Эти уравнения удобно представить в матричной форме (сводка обозначений и сведения из теории матриц даны в Приложении).

(3.6)

,

где Т – знак транспонирования.

Система (3.6) может быть записана в сжатой форме

(3.7)

где - векторная переменная, называемая вектором состояния;

U, y – скалярные переменные;

А – квадратная матрица коэффициентов размерностью n x n;

B – матрица-столбец размерностью n x 1;

С – матрица-строка размерностью 1 х n.

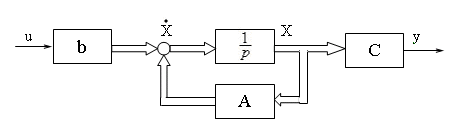
Рис. 3.2. Структурная схема описания n-ого объекта с

использованием вектора состояний Х

Матрица А называется переходной или собственной матрицей объекта, матрицы B и С соответственно – входной и выходной матрицами. Система (3.7) подобна по форме системе (3.3). Соответственно она имеет подобную структурную схему (рис. 3.2). Отличие заключается в замене скалярной величины х вектором Х и заменой коэффициентов матрицами. Широкой стрелкой обозначаются направления действия векторных величин, узкой – скалярных.

В качестве примера рассмотрим описание электрического четырехполюсника, представленного на рис. 3.3, через координаты состояния.

Рис. 3.3. Электрическая схема четырехполюсника

За координаты состояния примем напряжения на конденсаторах

(3.8)

Исходя из схемы на рис. 3.3 можно записать следующие уравнения равновесия

Учитывая, что

и введя обозначения (3.8), получим

Представим эту систему в виде (3.4)

(3.9)

или в матричной форме, как система (3.6),

(3.10)

Структурные схемы четырехполюсника, соответствующие системам (3.9) и (3.10), представлены соответственно на рис. 3.4,а и рис.3.4,б.

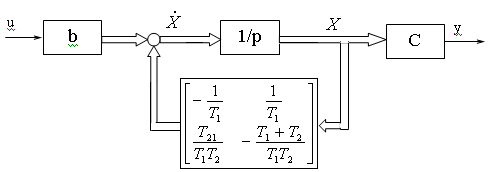
а)

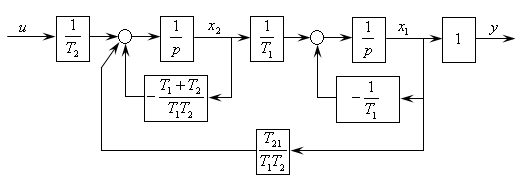
б)

Рис. 3.4 Структурная схема четырехполюсника

а) в матричной форме, б) в структурно-операторной форме

В качестве второго примера, рассмотрим электродвигатель постоянного тока, который наиболее часто применяется в качестве исполнительного устройства.

Запишем уравнение механического равновесия для электродвигателя в соответствии со вторым законом Ньютона

Уравнение движущего момента по закону Фарадея

Уравнение Кирхгофа для напряжений в якорной цепи двигателя

В этих уравнениях обозначено L, R – индуктивность и сопротивление якорной цепи;

Се, С_М – конструктивные постоянные двигателя.

Из уравнений не сложно получить систему в форме Коши (3.4)

(3.11)

Обозначив внешние воздействия через u₁ = u; u₂ = M_H; выходные сигналы через y₁ = : y₂ = , и взяв за координаты состояния следующие сигналы x₁ = ; x₂ = ; x₃ = I, получим систему вида (3.6):

(3.12)

В отличие от (3.6) в системе (3.12) входные и выходные сигналы представлены двухмерными векторами.

Соответствующую размерность имеют и коэффициенты матрицы В и С.

Электродвигатель можно представить также относительно скалярных величин входа и выхода. Для этого за выходную координату принимается одна переменная – угол поворота , а внешние воздействия разделяются на два класса: управляющие u и возмущающие f. В этом случае система (3.7) приобретает следующий вид:

(3.13)

В рассматриваемом примере u = U_Я; f = M_H – скалярные величины.