Приложение 1

Действия с матрицами

Матрица - это таблица чисел или объектов другой природы. Следовательно, ее можно представить как таблицу, состоящую из m строк и n столбцов, или матрицу размером m×n или (m×n) - матрицу. Числа или другие объекты, находящиеся в клетках таблицы, называются элементами а_ij.

		a11	а12	…	a1n
		a21	a22	…	a2n
A	=	a31	a32	…	a3n
		…	…	…	…
		am1	am1	…	amn

Матрица размером n×n называется квадратичной, матрица размером 1×n –матрицей столбцом, или вектором.

Матрица, у которой все диагональные элементы (числа) равны единице, а остальные равны нулю, называется единичной

.

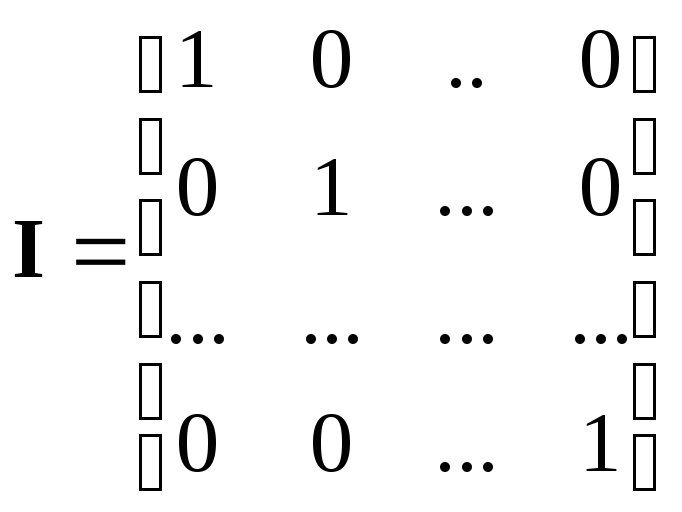Сложение матриц. Сумма двух матриц одинаковых размеров является матрицей такого же размера, у которой элементы определяются как c_ij= a_ij + b_ij.

Операция сложения матриц коммуникативная

.

Умножение матриц. Умножение на число ,

где

то есть каждый элемент умножается на данное число . Очевидно, что

.

Умножение матриц возможно, если число столбцов множимого равно числу строк множителя.

Произведением матрицы размером (m×n) на матрицу (n×r) является матрица размером (m×r), текущий элемент которой c_ij равен сумме произведений элементов i-й строки матрицы на соответствующие элементы

j-го столбца матрицы, то есть

.

Возможные варианты представлены в следующих схемах

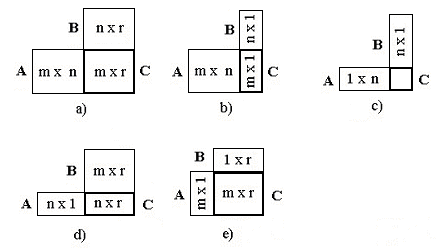
В результате умножений можно получить матрицу размером m×r (варианты а, е), матрицу-столбец (случай b), скалярную величину (случай с) и матрицу-строку (случай d).

Операция умножения матриц не подчиняется коммуникативному закону

.

Транспонирование матриц. Преобразование матрицы А, заключающееся в замене строк столбцами (или столбцов строками) при сохранении их нумерации, называется транспонированием. Транспонированная матрица обозначается А^Т. В транспонированной матрице А^Т диагональные элементы будут такими же, как в исходной матрице, а остальные элементы зеркально меняются, то есть матрица при транспонировании как бы переворачивается вокруг своей диагонали.

Определитель матрицы. Определитель (детерминант) матрицы А представляет число (числовую функцию), которое определяется по правилу, связанному с решением системы линейных уравнений. Для системы второго порядка

.

Для системы третьего порядка

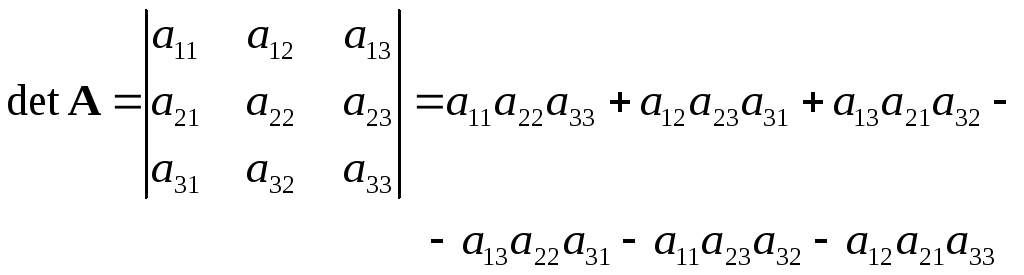
Правила вычисления определителей (детерминантов) дано в [5].

Важное свойство определителей: определитель матрицы А равен определителю транспонированной матрицы А^Т

.

Миноры и алгебраические дополнения. Эти понятия введены также для получения решения системы уравнений в общем виде.

Если в определителе n-го порядка выделить k различных строк (k≤n) и столько же различных столбцов, то элементы на пересечении этих строк столбцов образуют определитель, называемый минором. Очевидно, что минор n-го порядка совпадает с определителем. Если удалить из определителя строки и столбцы, участвующие в формировании минора, то оставшиеся элементы образуют определитель (n-k)-го порядок, называемый дополнением.

Миноры, образованные строками и столбцами с одинаковыми номерами, называются главными. Их диагональные элементы совпадают с диагональными элементами определителя.

Линейные преобразования. Систему уравнений n-го порядка

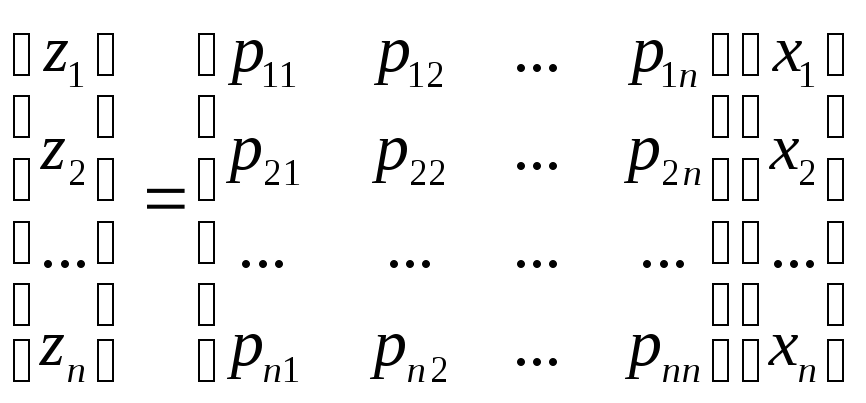. (п.1.1)

можно рассматривать как линейное преобразование совокупности переменных х₁, х₂ …, х_n в совокупность переменных y₁, y₂ ..., y_n. В матричной форме система (п.1.1) имеет вид

. (п.1.2)

Такие линейные преобразования используются для перехода описания объекта из одного координатного базиса (системы переменных) к другому базису.

Обратная матрица. Система n уравнений, определяющая переменные х_i, в матричном виде записывается следующим образом

. (п.1.3)

Умножим обе части этого уравнения на обратную матрицу А^-1

.

Определив, что , получим решение уравнения (п.1.3)

.

Следовательно, обратную матрицу можно определить из правила решения системы n уравнений с n неизвестными называется присоединенной матрицей.

. (п.1.4)

где

.

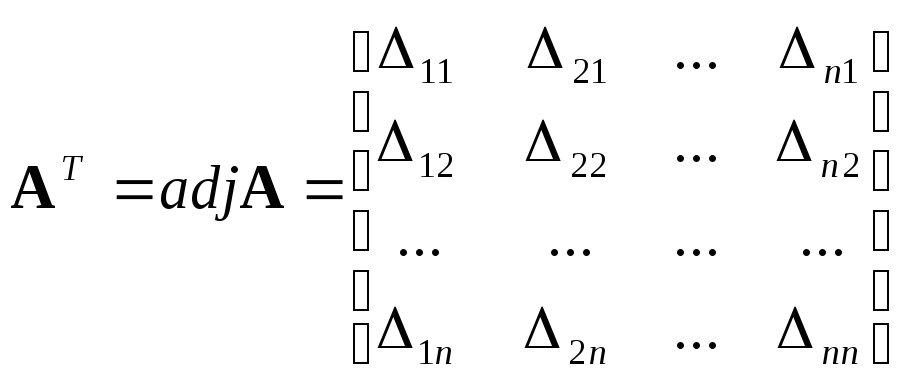Эта матрица представлена из алгебраических дополнений Δ_ij.

Таким образом, последовательность действий определения обратной матрицы будет следующей: элементы a_ij исходной матрицы заменяются их алгебраическими дополнениями Δ_ij; матрица алгебраических дополнений транспонируется, то есть получается присоединенная матрица adjA; вычисляется detA,- и присоединенная матрица умножается на величину, обратную detA.

Дифференциальные уравнения в матричной форме, описывающие динамику объекта, имеют следующий вид

. (п.1.5)

Его решение

,

где X₀ – вектор начальных условий, – матрица динамики свободного движения.

Алгебраизируем уравнение (п.1.5), подвергнув его преобразованию Лапласа,

. (п.1.6)

Уравнение выхода объекта управления

. (п.1.7)

Уравнение (п.1.6) представим в виде

.

Тогда решение дифференциального уравнения в соответствии с (п.1.4) будет

.

Для выходного сигнала с учетом (п.1.7), получим

.

Следовательно, передаточная функция объекта будет определяться следующим выражением

, (п.1.8)

где - характеристический полином передаточной функции.

Приложение 2