2. Коммуникационные тракты

2.1. Общие свойства

В электротехнике — это провода.

Для передачи сигнала нужны2 провода.

При условии провода с нулевым сопротивлениемэквипотенциальны.

Напряжение и ток не зависят от координаты, и скорость распространения сигнала считается бесконечной (ограничеие скоростью света несущественно).

Потери:

- сопротивление проводов R;

- проводимость изолятора G;

- излучение.

Потери на излучение растут с ростом частоты и определяют . Рабочая полоса частот:

.

Воптикесигналы распространяются непосредственно через среду (в том числе через вакуум).

Скорость волны:

;;.

Ф/см;Гн/см;

см/с.

Плотности энергии электрического и магнитного полей одинаковы:

. Отсюда:;.

Здесь

Ом —волновое сопротивление вакуума; (2.1.1)

—волновое сопротивление среды. (2.1.2)

Потери:

- в вакууме потерь нет на всех частотах .

- в среде потери на поляризацию (мнимые части и).

В технике СВЧ — сигналы передаются поволноводам. Волноводами могут быть и обычные провода, но в них слишком великипотери на излучение. Кроме того, провода неэффективны из заскин-эффекта(на высокой частоте работает только очень тонкий слой поверхности проводника; толщина этого скин-слоя уменьшается с ростом частоты, соответственно сопротивление возрастает).

СВЧ-волноводы ограничивают электрическое и магнитное поля в двух измерениях; при этом волна сигнала распространяется в 3-м измерении. Проще всего ограничивать поля с помощью металла.

2.2. Коаксиальный волновод

Самый привычный тип волновода — коаксиальный.

Как и в пустом пространсте, в нем могут существовать волны типаTEM (transverse electro - magnetical — поперечные электрические и магнитные поля).

Если волна распространяется направлении оси z, тоE_z = 0, Н_z = 0.

Коаксиальный волновод относится к классу непредельных — он пропускает все низкие частоты до .Широко используется даже на низких частотах для экранизации от помех.

Общий метод анализа волноводов — решение уравнений Максвелла при (нет зарядов) с граничными условиями на поверхности металла:

E_ = 0; Н_ = 0.

Волну TEMв непредельном волноводе можно проанализировать какдлинную линию с помощьютелеграфных уравнений. В идеальном волноводе без потерь — 2 параметра:

или

Здесь — погонные значения емкости и индуктивности,— волновое сопротивление. Как мы увидим ниже,— скорость волны.

Отсюда:

Распределеннаяэквивалентная схема:

Телеграфные уравнения:

; (1)

. (2) Дифференцируем 1-е уравнение по, а 2-е по.

Исключая или, получим:

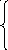
;; (3)

;. (4)

Уравнения (3) и (4) называются волновыми уравнениями. Они имеют решения в видеплоской волны. Для напряжения:

, (2.2.7)

где — волновое число. Тогда

; (5); (7)

; (6). (8)

Подставляя (7) и (8) в (3), получим закон дисперсии:

. (9)

Групповая и фазовая скорости волны определяются из (9):

. (10)

Это означает, что сигнал любой формы(т.е. суперпозиция любых гармоник)распространяется без искажений со скоростью ,которая определена в (2.2.4).

Таким образом, введенный в (2.2.4) параметр действительно имеет смысл скорости волны.

Знак «» в (10) означает, что волна может двигаться вдоль осиили в противоположном направлении.

Уравнение (4) для тока совпадает с уравнением (3) для напряжения. Поэтому для тока также существует решение в виде плоской волны:

. (2.2.8)

Тогда

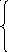; (11)

. (12)

Подставляя (11) и (6) в (1), получим: ;.

Согласно (9) и (2.2.4): . Таким образом,

. (2.2.9)

Отношение напряжения к току не зависит от времени и координаты и равно волновому сопротивлению , определенному в (2.2.1).

Вернемся к соотношениям (2.2.5) и (2.2.6):

Скорость волны не зависит от геометрических параметров . Она определяется только свойствами диэлектрика, а именно коэффициентом преломления . Более того,скорость волны вообще не зависит от формы и размеров поперечного сечения волновода.Она равна скорости света в диэлектрике.

В таких волноводах скорость волны одинакова.

Волновое сопротивление коаксиального волновода зависит от отношения логарифмически, т.е при большом значении— очень слабо.

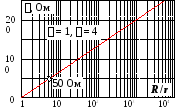
₀ = 377 Ом. При= 1,= 4:

Ом.

Удобно делать Ом; при этом:

;

1,3 пФ/см;3,3 нГн/см.

Практически сделать

Ом нельзя.

Энергии электрического и магнитного полей в волноводе одинаковы:

;;

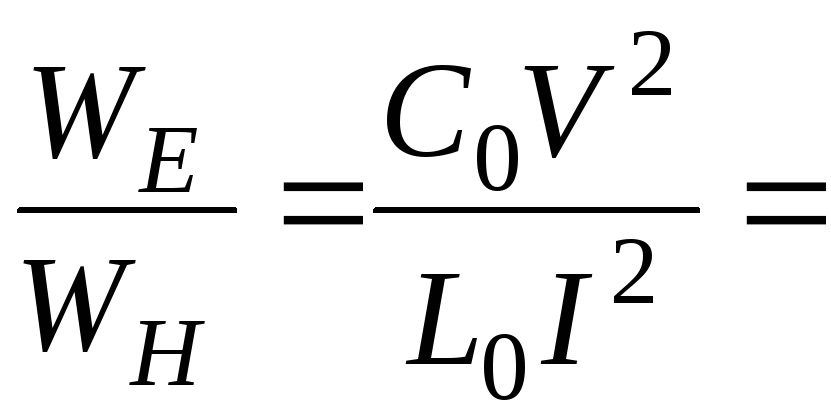
(как и в вакууме).

Сравнение коаксиального волновода с вакуумом:

Параметр	Вакуум	Коаксиал
	Формула	Формула	Примечание
Тип волны	ТЕМ	ТЕМ	—
Скорость волны		=	Не зависит от геометрии
Волновое сопротивление			Зависит от геометрии