
dsd1-10 / dsd-06=Kruglov+АИС / PDF / 7_Discretization_Z-TransferTheory
.pdf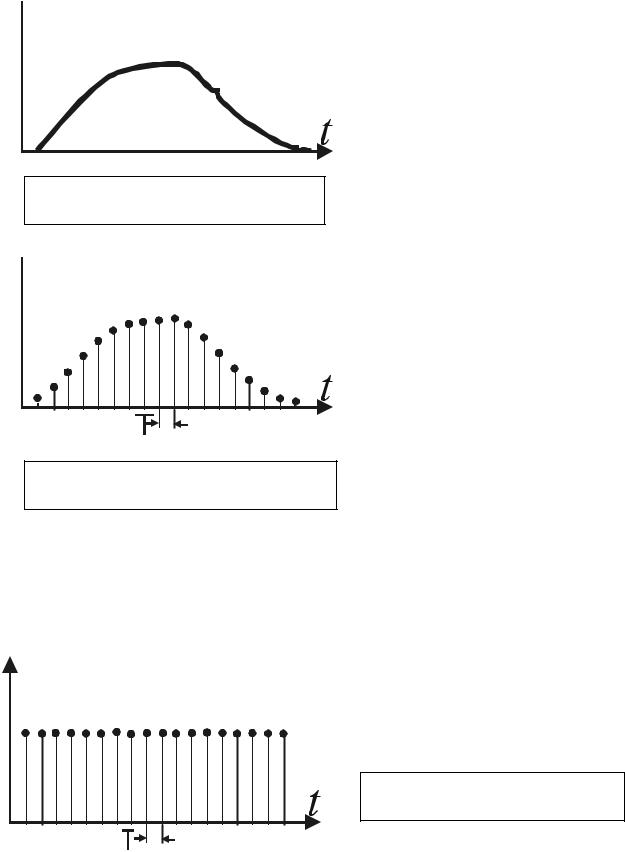
СПЕКТРЫ ДИСКРЕТИЗИРОВАННЫХ ВО ВРЕМЕНИ СИГНАЛОВ
Поскольку концепция Переключаемых Конденсаторов ПК) содержит дискретизацию
во времени, необходимо учитывать эффекты, являющиеся следствием дискретизации.
 X (t) Пусть имеем непрерывный во времени
X (t) Пусть имеем непрерывный во времени
сигнал X(t) (Рис. 3.5.), подаваемый на дискретно – аналоговую систему, на
входе которой стоит дискретизатор, представляющий на выходе системы сигнал в дискретном во времени виде
с промежутком времени Т (период) между дискретами (Рис.3.6.).
Дискретизированный во времени
Рис.3.5. Непрерывный во времени сигнал X(t)
сигнал X #(t) можно представить в виде произведения X (t) на некую
функцию S(t) ,оставляющую у
 X #(t)
X #(t)
X (t) значения только в
моменты nT , где n – целое Рис.3.6. Дискретизированный во число:
времени сигнал X#(t)
X #(t) = X (t) S(t) .
Периодичность функции S(t) однозначно характеризуется возможностью
разложения ее в ряд Фурье:
S(t) = |
∞ |
jnω st |
||
Cne |
||||
, где |
||||
S(t) |
|
n=−∞ |
||
2π |
|
|||
|
|
|||
ω s = |
. |
|
||
T |
|
|||
|
|
|
||
Рис.3.7. Дискретизирующая функция

Итак:
|
|
|
|
∞ |
|
|
∞ |
|
|
|
|
|
|
X #(t) = X (t) Cne jnω st = Cn X (t) e jnω st |
|
|
|||||||||||
|
|
|
|
n=−∞ |
n=−∞ |
|
|
|
|
|
|
||
Определим спектр сигнала X #(t) , для чего произведем его Фурье – |
|
|
|||||||||||
преобразование: |
|
|
|
|
|
|
|
|
|
|
|||
|
∞ |
|
∞ |
|
|
|
|
|
∞ |
|
|
|
|
X ( jω ) = |
|
C |
|
X (t) |
dt= |
( |
C |
X (t) e− j(ω −nω s )t |
) |
dt |
|||
|
|
n |
e− jω te jnω st |
||||||||||
|
|
|
|
|
n |
|
|
||||||
|
t=−∞ n=−∞ |
|
|
|
|
|
=t −∞ |
|
|
|
|
||
Поскольку e− jω t не зависит от n, умножим на эту величину каждый член ряда:
|
∞ |
|
|
∞ |
|
∞ |
|
|
|
|
|
|
|
|
|
n |
|
|
|||
X ( jω ) = |
X #(t) e− jω t dt= |
|
|
X (t) e jnω st |
|
e− ωj t dt |
||||
|
|
n=−∞ |
C |
|
||||||
|
t=−∞ |
|
|
=t −∞ |
|
|
|
|||
Сомножитель e− j(ω −nω s )t |
задает зависимость результата от частоты. Очевидно, |
|||||||||
что результат зависит от значения (ω − nω |
s ) , которое принимает одни и те же |
|||||||||
значения при частотах ω |
, периодически изменяющихся с периодом ω s . |
|||||||||
Другими словами, спектральная характеристика дискретизированного во времени
сигнала X #(t) имеет периодический вид.
X ( jω )
|
|
|
|
|
|
|
|
|
|
|
|
F = |
1 |
2F = |
2 |
|
|
||
|
|
|
|
||||||
|
|
S |
|
T |
S |
|
T |
||
|
Рис.3.8. |
Спектральная характеристика дискретизированного во времени |
|||||||
|
сигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДИСКРЕТИЗАЦИЯ И Z – ПРЕОБРАЗОВАНИЕ
Излагая введение в Z – преобразование, будем следовать монографии […].
Рассмотрим дискретизирующую схему
на Рис.3.9. Ключ S1 моментально
заряжает конденсатор С до
мгновенного значения входного
сигнала f (t) в моменты Т, 2Т, 3Т, … .
Это значение f (nT ) сигнала
Рис.3.9. Дискретизирующая схема |
τ , и |
держится в течение времени |

затем ключ S2 мгновенно разряжает конденсатор до нуля (см. Рис.3.10). На выходе дискретизатора находится
буфер с коэффициентом усиления К. Определим ступенчатую функцию u(t) . Пусть u(t) = 0 при t < 0 и
u(t) = 1 при t ≥ 0 . Тогда, согласно
 Рис.3.10, n – й отсчет функции f (t) можно представить в виде:
Рис.3.10, n – й отсчет функции f (t) можно представить в виде:
Рис.3.10. Дискретизированный
эквивалент непрерывной функции
fn (t) = K f (t)[u(t− nT )− u(t− (nT+ τ ))] . |
f (nT ) |
|||||||||||||
|
|
|||||||||||||
Предполагая f (t) = 0 при t < 0 , дискретизированный эквивалент |
f * (t) этой |
|||||||||||||
функции можно записать: |
|
|
|
|
|
|
|
|
|
|
(3.11) |
|||
|
|
∞ |
∞ |
|
|
|
|
|
|
|
|
|
))] |
|
f * (t) = fn (t) = K f (nT ) [u(−t nT )− |
|
u(−t (nT+ τ |
|
|||||||||||
|
|
n=0 |
n=0 |
|
|
|
|
|
|
|
|
|
|
|
Произведем для |
f (t) преобразование Лапласа и найдем изображение F (s) . |
|||||||||||||
Учитывая что f (t − a) |
e−as F(s) , а также u(t) |
1 , |
получаем: |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
∞ |
1 |
− snT 1 |
|
− s |
nT +τ |
) |
|
|
1 − e− sτ |
∞ |
− snT (3.12) |
|
F |
(s) = K f (nT ) |
e − |
e |
( |
|
|
K |
|
|
F (nT )e |
||||
|
|
|
= |
s |
||||||||||
|
|
n=0 |
s |
s |
|
|
|
|
|
|
|
n=0 |
|
|
Пусть ширины τ |
импульсов, представляющих функцию |
f * (t) , очень малы, тогда |
||||||||||||
в (3.12) можно записать: |
|
|
|
|
|
|
|
|
|
|
|
|||
K |
1 − e− sτ |
≈ K |
|
s |
|||
|
|
Для выражения для F (s)
1− (1− sτ ) |
|
s |
= K |
|
|
положим K = τ1
τ . |
(3.13) |
. Итак, не амплитуда, а площадь
каждого импульса функции f (t) |
равна |
f (nT ) , и выражение (3.12) записывается |
|
в виде: |
|
|
|
∞ |
|
∞ |
|
F (s) = f (nT ) |
e− snT = |
z− n ≡ F(z) , |
(3.14) |
n=0 |
|
n=0 |
|
где z = esT .
Выражение (3.14) называется Z – преобразованием дискретных выборок
f (nT )
функции f (t) .

Поскольку Z – преобразование является таким же интегральным преобразованием, как и преобразование Лапласа, все свойства Z – преобразования повторяют
свойства преобразования Лапласа, но с учетом (3.14), т.е. z = esT .
Определим два важных дискретных сигнала – две последовательности.
1)последовательность «единичный импульс» δ (n) , определяемая следующим образом:
δ (n) = 0 при n ≠ 0 и δ (n) = 1 при n = 0 |
(3.15) |
Непрерывный сигнал x(t) , подвергнутый дискретизации и представленный
мгновенными выборками в моменты времени 0, Т, 2T, 3T, … nT, … можно
выразить через последовательность «единичный импульс» следующим образом:
∞
x(n) = x(k) δ (n − k)
k=−∞
2)последовательность «единичный скачок» u(n) , определяемая
следующим образом:
u(n) = 1 при n ≥ 0 и u(n) = 0 при n < 0
(3.16)
(3.17)
Из определений (3.15) и (3.17) можно показать, что последовательности единичный импульс и единичный скачок связаны соотношениями:
∞
u(n) = δ (k)
k=−∞
δ(n) = u(n) − u(n −1)
(3.18а)
(3.18б).
Пусть h(n) - отклик линейной системы при всех нулевых начальных условиях на
единичный импульс δ |
(n) . Тогда последовательность h(n − k) |
является |
откликом на δ (n − k) . |
Из линейности системы и входной последовательности |
|
(3.16) выходная последовательность задается выражением: |
|
|
|
∞ |
|
y(n) = x(k) h(n − k) |
(3.19а) |
|
k =−∞
Это означает, что линейная дискретная во времени система характеризуется
ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКОЙ h(n) , т.е. выходной последовательностью
при единичном импульсе на входе и нулевых начальных условиях. В уравнении
(3.19а) можно заменить переменную, результат при этом не изменится:
∞ |
|
y(n) = x(n − k) h(k) |
(3.19б) |
k =−∞
Оба уравнения (3.19а) и (3.19б) обозначают СВЕРТКУ двух последовательностей
x(n) и h(n) .
Линейная система называется УСТОЙЧИВОЙ, если импульсная характеристика h(n) удовлетворяет условию:
∞ |
|
h(n) < ∞ |
(3.20) |
n=−∞
и ФИЗИЧЕСКИ РЕАЛИЗУЕМОЙ, если
h(n) = 0 для n < 0 . |
(3.21) |
