Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5_ARC_SC_Biquad

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

325.91 Кб

Скачать

☆

ВВЕДЕНИЕ В ARC РЕАЛИЗАЦИЮ БИКВАДА

Известно, что передаточная функция (ПФ) фильтра в общем выражается отноше-

нием полиномов: H (s) =	a	N	sN + a	N −1	sN −1 + a	N −2	sN−2 + ..... + a s + a	0
							1
		bL sL + bL−1sL−1 + bL−2 sL−2 + ..... + b1s + b0							(3-1)

(3-1), где, как правило, L ≤ N . При действительных коэффициентах корни поли-

номов могут быть либо действительными, либо комплексно–сопряженными, поэтому одним из способов реализации фильтра является разложение на произведение М простых дробей, в которых числители и знаменатели являются полиномами не

выше второго порядка:

H (s) = a21s2 + a11s + a01 × b21s2 + b11s + b01


a s2 + a s + a			×	...×	a s2 + a s + a			(3-2).
b22 s2	+ b12 s + b02				b2M s2	+ b1M s + b0M
22	12	02			2M	1M	0M

Как интерпретировать такой вид ПФ? Рассмотрим систему, в которой друг за

другом включены М подсистем, так что выход предыдущей является входом последующей. Тогда ПФ системы равна:

H (s) =

V (1)

(2)

(M )

V (1)

V (2)

V (M )

H× 1(s× ) ... HM (s)

OUT

× ...×

OUT

≡

OUT ×

OUT × × ...

OUT =

VIN (1)

VOUT (1)

VOUT (M −1)

VIN (1)

VIN (2)

VIN (M )

(3.3)

Из выражения (3.3) очевидно, что если ПФ всей системы равна произведению всех ПФ всех подсистем, то подсистемы включены последовательно друг за другом.

Итак, необходимо уметь реализовать подсистему фильтра, описываемого рациональной дробью с числителем и знаменателем 2 – го порядка. Такой фильтр называется биквадом.

	H(s) =	VOUT (s)	= − a2s2 +a1s+a0
Имеем ПФ биквада:		V (s)	b s2	+bs+b .	(3-4).
		IN	2	1 0

Знак «минус» перед дробью не играет принципиальной роли, но с ним реализация получается проще.

В дальнейшем в записи ПФ биквада будем следовать традиции, сформировавшей-

ся при решении в электротехнических задачах дифференциальных уравнений второго порядка:

Ha (s) =

+ K s + K

Итак, имеем:

(3.5)

s + ω

Здесь ω 0 - частота полюса и Q - добротность по-

люса

в выражении для Ha (s) . Предполагается, что в

общем случае полюс sp есть

комплексное число

sp = σ

p + ωj p и сопряженное к нему.

Вводятся определения:ω

= σ

p2 ω+ p2

Рис.3.1. Иллюстрация опре-

делений для выражения 3.6.

Рис.3.2. Активный интегратор с токовым входом

= 1

Q =

1 +

(3.6)

На Рис. 3.1. изображена комплексная s – плоскость, иллюстрирующая определения (3.6). Если Q велика (порядка 10 или больше), полюс относительно близок к

jω - оси. При этом Ha ( jω ) имеет острый пик около ω 0 . Перепишем (3.5) в виде:

s2V

= −(K

s2 + K s

+ K

−

ω 0 s + ω

out

out .

Делим обе части на s2 и проводим перекомпоновку:

= − 1

+ K

s)V

+ ω 0 V

− ω

, где

V = − 1

K0 V

+ω

out

0 1

ω 0

0Vout (3.7)

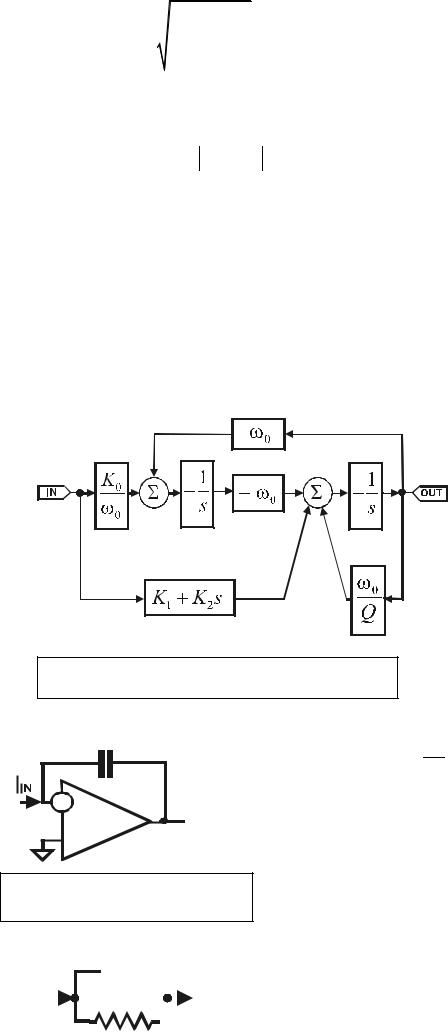
Функциональная схема биквада, описываемая уравнением (3-7), приведена на Рис. 3-1.

Рис.3-1. Функциональная схема биквада

ставляющей напряжение

IIN = −sCVOUT ; H (s)

Найдем электротехническое воплощение алгебраических многочленов в фор-

муле (3-5) и на Рис.3-1. Для

этого отметим, что при записи уравнений Кирхгофа узел А инвертирующего входа ОУ в активном инте-

граторе вместе с интегри-

рующим конденсатором С выполняет роль коллектора токов компонентов, подклю-

ченных к этому узлу.

Найдем ПФ интегратора с входной

переменной, представляющей ток IIN и выходной переменной, пред- VOUT (см. Рис.3 -2.). Итак:

= − sC1 . Если C = 1 , то H (s) = − 1s ,

что и требовалось.

Теперь найдем ПФ параллельной RC цепочки, но, наоборот, с

V напряжением на входе и с током на выходе. Дополнительное OUT условие: потенциал токового выхода поддерживается равным нулю, предполагая, что он должен быть подключен к инвер-

тирующему входу идеального RC интегратора с токовым входом на Рис. 3.2. Итак, имеем:

= 0) = VIN + sCV

IN , и

H (s) =

IOUT

+ sC

IOUT

OUT

VIN

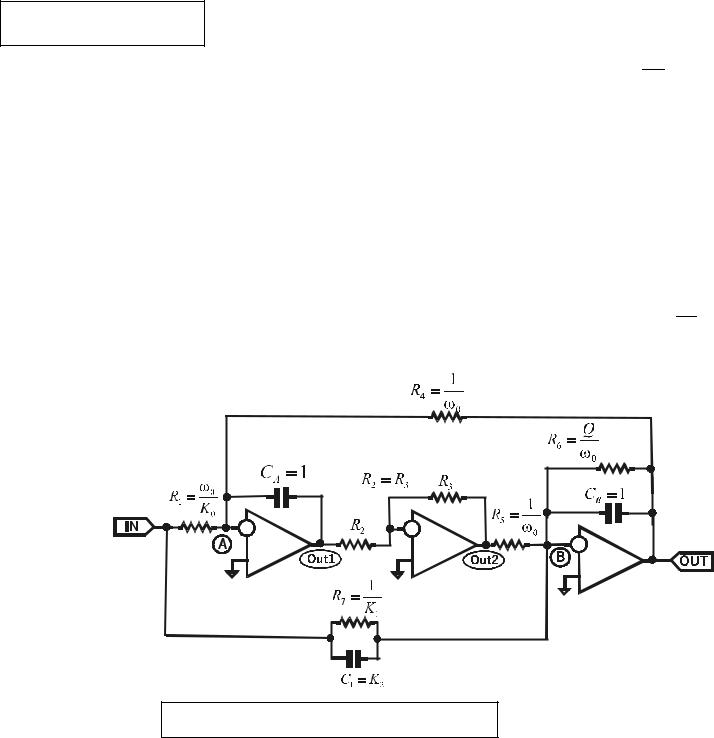
Рис.3.3. Параллельная

RC цепочка

Сравниваем со схемой на Рис. 3.1. и находим блок, содержащий многочлен переменной s. Поскольку коэффициент при переменной s обя-

зательно должен содержать емкость С, то делаем вывод, что коэф-

фициент K2 есть значение емкости, а свободный член K1 есть об-

ратное значение сопротивления, т.е. значение проводимости. Аналогично ω 0 и

	K0				1	ω 0
	ω 0 - также значения проводимостей, а				1	ω 0
	ω 0 - также значения проводимостей, а			ω	0	и K0 - значения сопротивлений. Со-
		−	1
гласно нашим рассуждениям, член		−	ω 0		является также значением сопротивле-
гласно нашим рассуждениям, член			ω 0		является также значением сопротивле-

ния, но отрицательным. Этот факт не должен вызывать затруднений, поскольку

это просто означает, что перед резистором с положительной величиной ω 0 дол-

жен находиться инвертор сигнала.

Рис.3.4. ARC реализация биквада

Итак, АRC реализация биквада приведена на Рис. 3.4.

Следует обратить внимание на то, что в ARC фильтрах ведущую роль играют АКТИВНЫЕ ИНТЕГРАТОРЫ, являющиеся основой элементной базы.

Разумеется, ни в интегральных ARC фильтрах, ни в фильтрах на дискретных ком-

понентах, не используют номинал С=1(F) конденсатора и R=1(Ohm) резистора. Существует метод так называемого масштабирования.

Запишем, например, для узла В уравнение Кирхго-

VIN −VB + sC (V −V

) + VOUT 2 −VB =

VB − VOUT

+ sC

(V −V

)

фа:

OUT

(3-8)

(напоминаем, что VOUT 2

= −VOUT1 ) .

Разделим обе части уравнения (3-6) на m и сгруппируем члены:

VIN

−VB + s

−V ) + VOUT 2 −VB =

VB −VOUT

+ s

(V −V

)

(mR7 )

(mR5 )

(mR6 )

OUT

(3-9)

Итак, уравнение (2-5) выражает правило:

Для установления реальных величин номиналов резисторов и конденсаторов, во всех ветвях, подходящих к узлу виртуальной земли, резисторы можно увеличить (уменьшить) в m раз, а конденсаторы – уменьшить (увеличить) также в m раз.

Однако, само по себе масштабирование не позволяет перешагнуть через физические ограничения на номиналы компонентов: интегральные конденсаторы трудно сделать емкостью, большей 50 пФ, а резисторы – больше 1Мом, при-

чем такие компоненты имеют громадные площади, поэтому с их помощью практи-

чески нельзя создать фильтры звуковых частот порядка более 3 – х. Концепция

переключаемых конденсаторов позволяет, во – первых, создавать низкочастотные фильтры большого порядка и, во – вторых, обеспечивать высокую точность частот срезов.

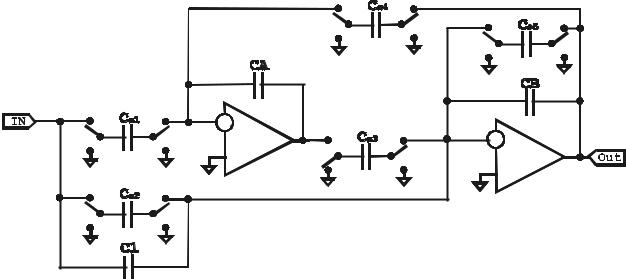
Реализация биквада путем прямой замены резисторов на ПК

Предположим, что резисторы имитируются переключаемым конденсатором (ПК) с частотой переключения Fs, много большей наивысшей частоты сигнала, поступае-

мого на вход фильтра. Тогда REFF =1/Cs*Fs. Здесь REFF – номинал эквивалентного резистора; СS – переключаемый конденсатор; FS – частота переключения. За-

меним каждый резистор на ПК, причем любой резистор с именем Ri заменим на ПК с именем СSi.

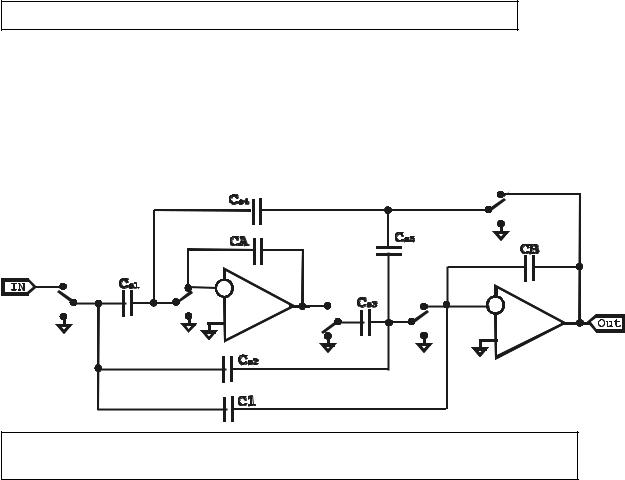
Рис.3.5. Схема биквада после прямой замены резисторов на ПК

Отметим , что все ПК не изолированы друг от друга . У некоторых ПК (CS1 и СS2), левые обкладки имеют одинаковый потенциал в любом из положений ключей ( 1

или 2) , что позволяет объединить "местные" ключи принадлежащие одному из ПК , в один общий , обслуживающий несколько ПК. Одинаковый потенциал имеют правая обкладка CS1 и левая обкладка CS4, правые обкладки CS2 и CS3 и левая обкладка

CS5, правые обкладки CS4 и CS5. Благодаря этому счастливому обстоятельству, схему можно перерисовать в виде:

Рис.3.6. Упрощенная схема биквада после объединения узлов с одинаковыми потенциалами.

Отметим значительную экономию количества ключей . В результате данная схема

имеет каноническую конфигурацию биквада на ПК.

Вернемся к замечанию по поводу знака передаточной функции биквада.

Если передаточная функция имеет вид :

H(S) =

V (S)

b s2

+b s +b 1

вых

V (S)

a s2

+ a s + a

,то после преобразований получим:

вх

b b

−

S V

−

0 V

вых

вх

вых

вх

вых

a2 a0

Как можно видеть , отрицательной величиной теперь является не только резистор

величины	a2	, но и конденсатор величины	b2	. И если отрицательный резистор
	b1		a2

можно реализовать просто в виде инвертирующего ПК , то для реализации отрицательного конденсатора в любом случае последовательно с ним должен находиться

инвертор. Это обстоятельство затрудняет реализацию неинвертирующего биквада,

если использовать классические ОУ, т.е. с одним выходом. При использовании

нового класса полностью дифференциальных ОУ дополнительный инвертор не нужен (см. рисунок ниже).

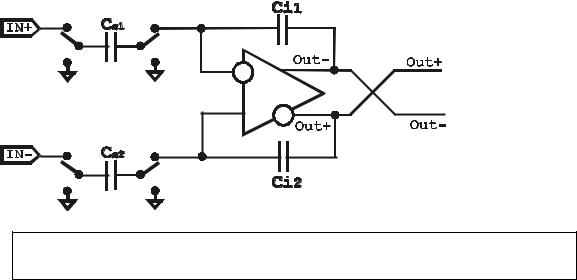
Рис. 3.7. Полностью дифференциальный интегратор на базе полностью дифференциального ОУ.

В полностью дифференциальных ОУ выходным напряжением является не напря-

жение между выходом и аналоговой землей, а между выходами, т.е. удваивает-

ся. При этом:

•2 раза увеличивается отношение сигнала с собственному шуму схемы;

•ввиду симметричной внутренней структуры ОУ теоретически устраняются все внешние наводки;

•увеличивается быстродействие ОУ.

Изложенные достоинства перекрывают недостаток, заключающийся в необходимости иметь в схеме почти в 2 раза больше ПК и интегрирующих конденсаторов.

Соседние файлы в папке PDF

#
05.06.2015258.01 Кб761_SimpleAmplifier.pdf
#
05.06.2015192.66 Кб732_SmallSignalCirCMOSAmp.pdf
#
05.06.2015252.74 Кб753_TransferFunctrion_OpAmsApps.pdf
#
05.06.2015363.2 Кб734_SC_Types.pdf
#
05.06.2015325.91 Кб745_ARC_SC_Biquad.pdf
#
05.06.2015404.43 Кб736_Noises.pdf
#
05.06.2015132.52 Кб747_Discretization_Z-TransferTheory.pdf
#
05.06.20151.05 Mб74KRUGLOV.pdf